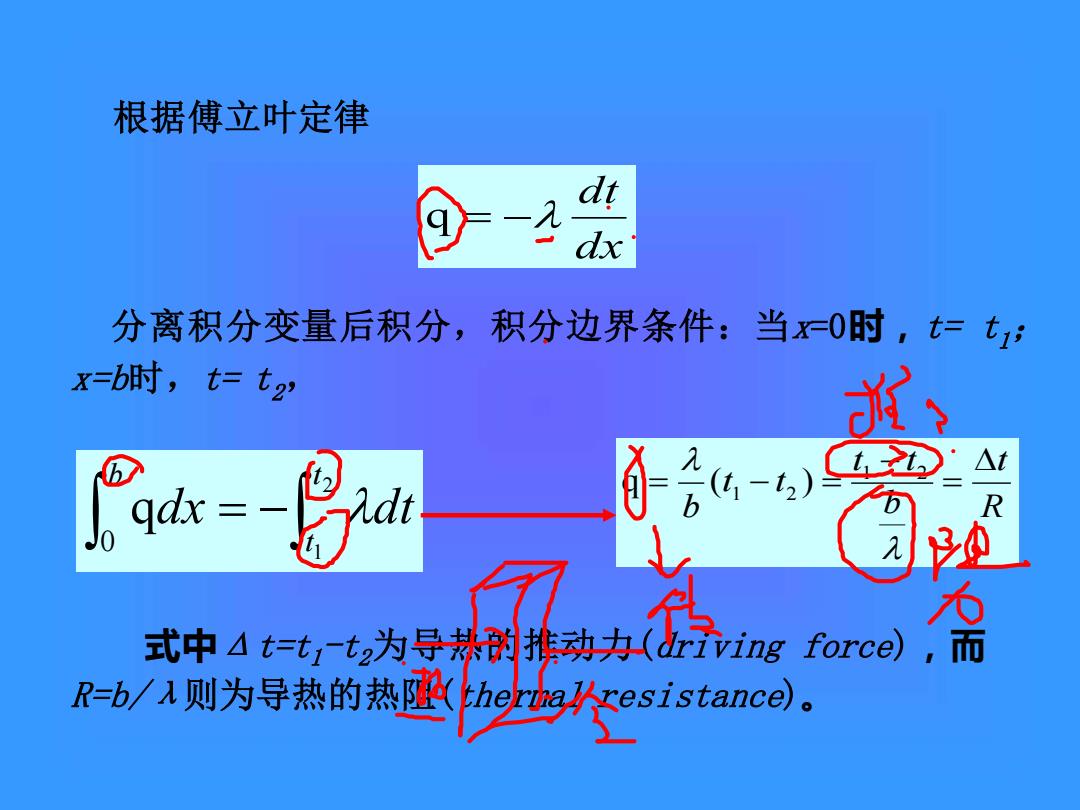
根据傅立叶定律 分离积分变量后积分,积分边界条件:当x0时,t=t: x=b时,tet2 的 R 式中4t达发房vin or四备 R=b/1则为导热的热坠herua!resistance)
dx dt q = − R t b t t t t b = − = − = 1 2 1 2 q ( ) 式中Δt=t1-t2为导热的推动力(driving force),而 R=b/λ则为导热的热阻(thermal resistance)。 根据傅立叶定律 分离积分变量后积分,积分边界条件:当x=0时,t= t1; x=b时,t= t2, = − 2 0 1 q t t b dx dt

讨论: 1.可表示为 △t 推动力 R 热阻 推动力:△t=(t1-t2》 b 热阻: R= 2.分析平壁内的温度分布 Qd=d 上限由 x=b时,t=2为x=x时,t=t qx X t =ti t1一 b
讨论: 热阻 推动力 = = R t q t = (t − t ) 1 2 b R = 2.分析平壁内的温度分布 = − 2 1 0 q t t b dx dt 上限由 2 x = b时,t = t x = x时,t = t x t t t t x q q ( ) = 1 − = 1 − 1.可表示为 推动力: 热阻: 为 x b t t t t 1 2 1 − = −

不随变化,~x成是线形关系。 若随变化关系为:=,1+at) 则t~x呈抛物线关系。 3.当随变化时 如:九1t1,2t2 1=(21+2)/2
不随t变化, t~x成呈线形关系。 (1 ) = 0 + at 3.当随t变化时 = ( + ) / 1 2 2 若随t变化关系为: 则t~x呈抛物线关系。 如:1 ~t 1,2 ~t 2
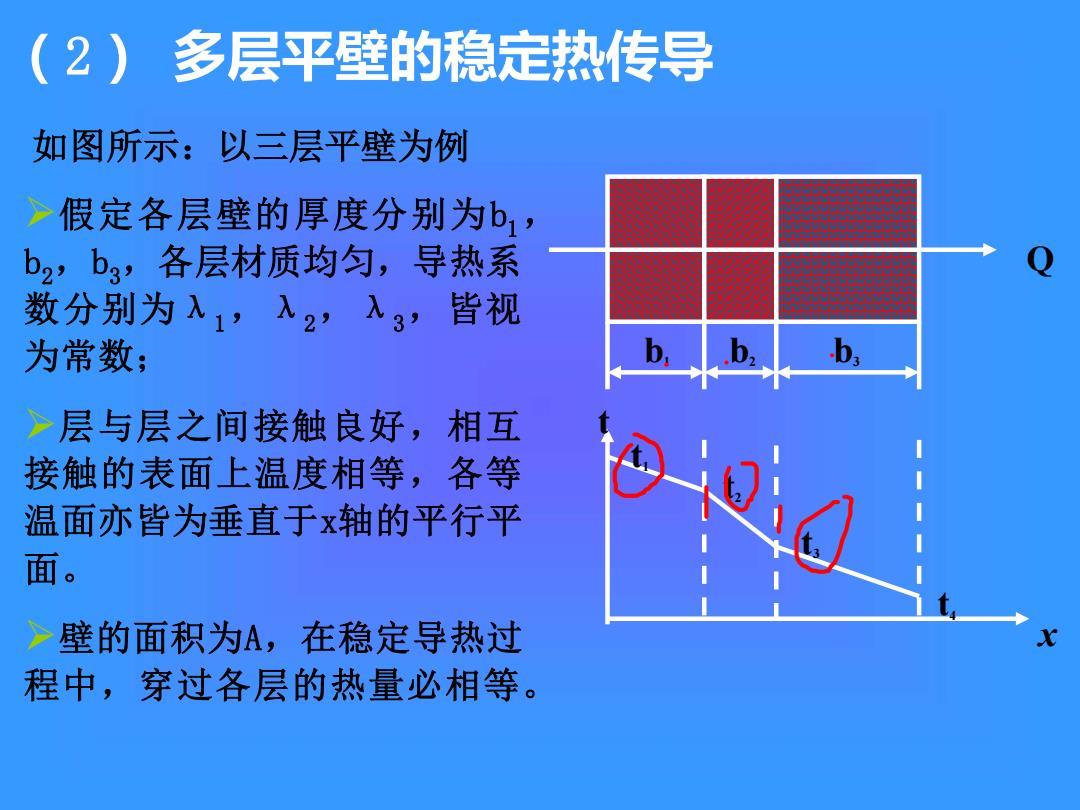
(2)多层平壁的稳定热传导 如图所示:以三层平壁为例 >假定各层壁的厚度分别为b1, b2,b3,各层材质均匀,导热系 数分别为入1,2’入3 皆视 为常数; >层与层之间接触良好,相互 接触的表面上温度相等,各等 温面亦皆为垂直于x轴的平行平 面。 >壁的面积为A,在稳定导热过 程中,穿过各层的热量必相等
如图所示:以三层平壁为例 Q b1 b2 b3 x t t1 t2 t3 t4 ➢假定各层壁的厚度分别为b1, b2,b3,各层材质均匀,导热系 数分别为λ1,λ2,λ3,皆视 为常数; ➢层与层之间接触良好,相互 接触的表面上温度相等,各等 温面亦皆为垂直于x轴的平行平 面。 ➢壁的面积为A,在稳定导热过 程中,穿过各层的热量必相等。 (2) 多层平壁的稳定热传导
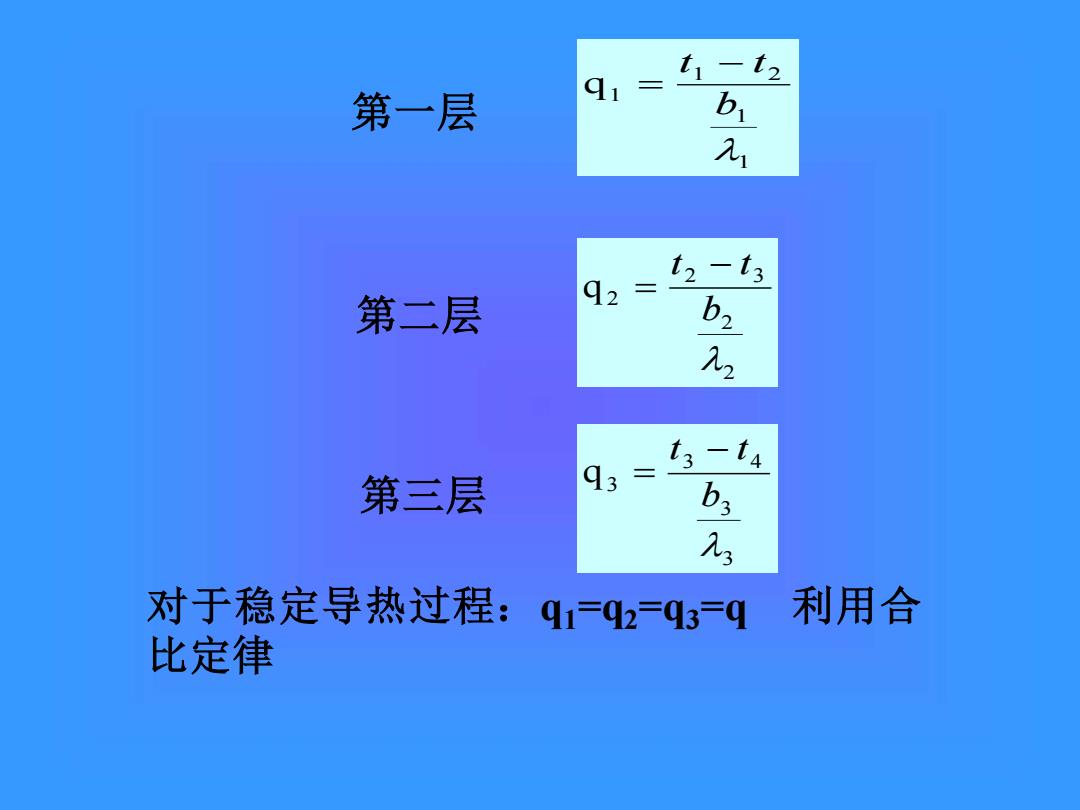
t1-t2 第一层 91s b 元 t2-t3 第二层 b2 2 第三层 93 t3-t4 b 对于稳定导热过程: q1=q2=q3=q 利用合 比定律
1 1 1 2 q1 b t − t = 3 3 3 4 q3 b t − t = 2 2 2 3 q2 b t − t = 第一层 第三层 第二层 对于稳定导热过程:q1=q2=q3=q 利用合 比定律