西安交通大学：《材料力学 Mechanics of Materials》课程教学资源（课件讲稿）第二部分 组合变形（共三章，主讲：殷民）

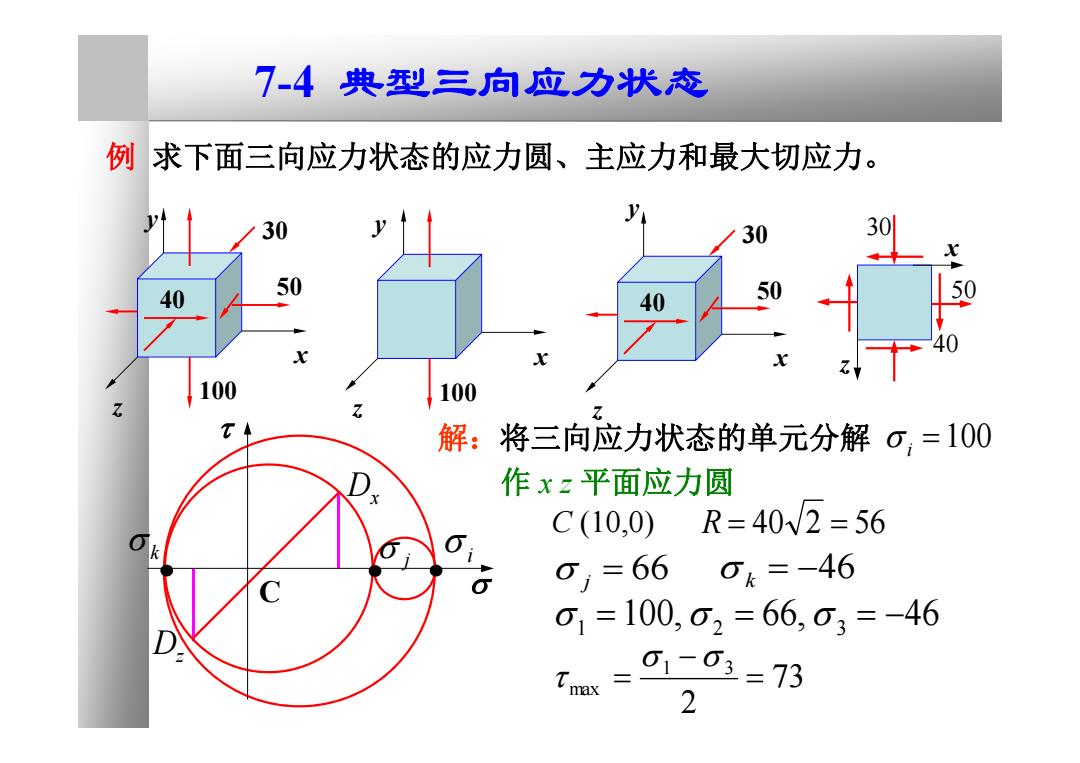
7-4典型三向应力状态 例求下面三向应力状态的应力圆、主应力和最大切应力。 30 30 30 50 40 40 50 100 100 7 解：将三向应力状态的单元分解σ=100 作xz平面应力圆 C(10,0) R=40W2=56 0,=66 0k=-46 01=100,02=66,03=-46 01-03=73 2

例 求下面三向应力状态的应力圆、主应力和最大切应力。 y x z 50 30 40 100 解：将三向应力状态的单元分解 100, 66, 46  1   2   3   Dx 作 x z 平面应力圆 Dz C  j  66  k  46   i   j  k C (10,0) R  40 2  56 73 2 1 3 max       y x z 100 y x z 50 30 40  100  i 50 40 30 z x   7-4 典型三向应力状态

7-5广义胡克定律 主应变Principal Strain):主应力方向上的应变 01020381E28381≥82≥83 O1单独作用 O)单独作用( 3单独作用 01 62 63 E E E E 63 &n 2 E E E 6 62 03 -u E E E 同时作用 81 01 E +(-“2)+(- E

 2  3  1 主应变(Principal Strain) ：主应力方向上的应变 1 2 3     1  2  3 1 2 3     E  1 E  2   1  2  3  E  3   E  1   E  1   E  2   E  2 E  3 E  3    1 单独作用  2 单独作用  3 单独作用 同时作用 ( ) ( ) 1 2 3 1 E E E         7-5 广义胡克定律