
7-3二向应力状态分析一—图解解析法 二、a截面上的应力如何在应力圆上得到? 从D点出发, Da 根据单元体a角 D.(Ox,Tx) 的转向,沿圆 周转动2a圆心 角,得到D点, 该点的坐标即 为a截面上的应 D,(oy,ty) 力。 = Cx Rcos(2a+2d0) C.Rcos2a cos2ao-Rsin 2a sin 2do o:-oy cos2a-t,sin 2a 点面对应, 2 2 转向一致, D a v ta(同理) 转角加倍
二、α截面上的应力如何在应力圆上得到? x y x y x y ( , ) Dy y y C ( , ) Dx x x 0 2 cos(2 2 ) D x Cx R 0 0 2 0 Cx Rcos2 cos2 Rsin 2 sin cos2 sin 2 2 2 x x y x y D 2 D y (同理) 点面对应, 转向一致, 转角加倍 从Dx 点出发, 根据单元体α角 的转向,沿圆 周转动2α圆心 角,得到Dα点, 该点的坐标即 为α截面上的应 力。 7-3 二向应力状态分析—图解解析法

7-3二向应力状态分析一图解解析法 三、应力圆上的主平面、主应力和极值切应力 2 max 主平面 D.(O:,Tx) tan200=- 2t 主应力 Ox-O 2 20 6c0 0±0y+ 2 D,(Ov,ty) 极值切应力 max 2+ min min tan 2a 此外,从应力圆上还可以得到: 2t. 极值切应力的作用面与主平面间的夹角是45度; 互相垂直的截面上,切应力等值反向,正应力之和为常数: 切应力最大与最小的截面上,正应力不为零,且两正应力大 小相等,符号一致
三、应力圆上的主平面、主应力和极值切应力 ( , ) D y y y C ( , ) D x x x 0 2 主平面 x y x 2 tan 2 0 0 2 2 ' ) 2 ( 2 0 0 x x y x y 主应力 0 ' min max 2 2 ) 2 ( x x y 极值切应力 max min 1 2 x x y 2 tan 2 1 ● 切应力最大与最小的截面上,正应力不为零,且两正应力大 小相等,符号一致。 ● 互相垂直的截面上,切应力等值反向,正应力之和为常数; 此外,从应力圆上还可以得到: ● 极值切应力的作用面与主平面间的夹角是45度; 7-3 二向应力状态分析 —图解解析法

7-3二向应力状态分析一图解解析法 87.75 例已经某单元体,试用图解解析法求解 .25 主应力、极值切应力的大小及方位。 解:0,=30,0,=60,t,=-t,=-40 画应力圆 30 D 2 主应力00=87.75 0x0=2.25 主平面a=号180°-acam-2)=5° a'0 a0 σ极值切应力 Imx =R=42.75 200 01=o+45°=100° 讨论:如何求解斜截面上的应力?
30 40 60 例 已经某单元体,试用图解解析法求解 主应力、极值切应力的大小及方位。 解: x 30, y 60, x y 40 画应力圆 主应力 87.75 2.25 0 '0 主平面 ) 55 2 (180 arctan 21 0 y x x 极值切应力 max R 42.75 45 100 1 0 Dy Dx '0 C 0 0 2 max ) 42.75 2 45 ( 2 2 2 x x y y x Cx R 87.75 2.25 讨论:如何求解斜截面上的应力? 7-3 二向应力状态分析—图解解析法

7-4典型三向应力状态 应力状态的分类:(不严格定义) 单向应力状态:某两对面上的应力为零 平面应力状态:某一对面上的应力为零 三向应力状态:各对面上的应力均不为零 应力状态的分类:(严格定义) 单向应力状态:非零主应力的个数为1 二向应力状态:非零主应力的个数为2 三向应力状态:非零主应力的个数为3 主单元体 按代数值排列三个主应力 01之02≥03
● 应力状态的分类:(严格定义) 单向应力状态:非零主应力的个数为1 二向应力状态:非零主应力的个数为2 三向应力状态:非零主应力的个数为3 ● 按代数值排列三个主应力 1 2 3 7-4 典型三向应力状态 ● 应力状态的分类:(不严格定义) 平面应力状态:某一对面上的应力为零 三向应力状态:各对面上的应力均不为零 单向应力状态:某两对面上的应力为零 主单元体
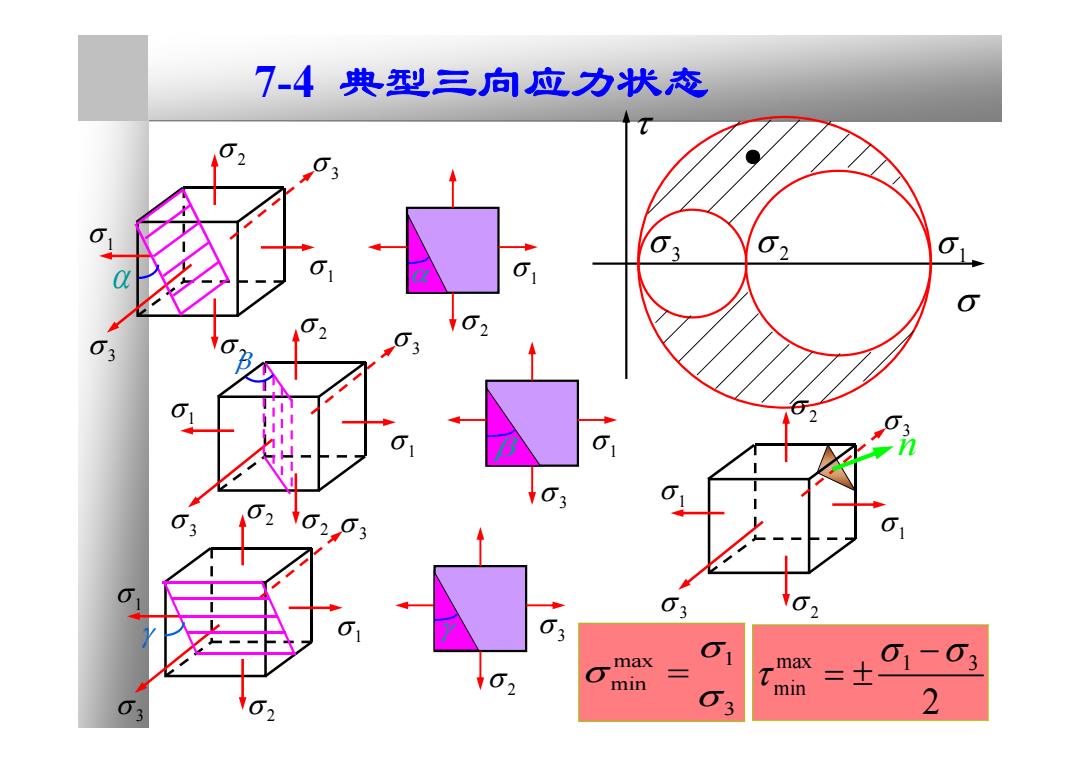
7-4典型三向应力状态 03 63 03 max max 01-03 62 O min min 63 62 3 2
2 1 1 3 2 3 1 2 2 1 2 1 1 3 2 3 1 3 3 2 1 1 3 2 3 3 2 2 1 1 3 2 3 n ● max 1 3 min 2 7-4 典型三向应力状态 max 1 min 3