3.2一阶系统的时域分析 y(t),u(t) u(t) T y(t) t 0 T 2023年7月24日4时48分 北京料技大学自功化学院自功化系 21
2023年7月24日4时48分 北京科技大学自动化学院自动化系 21 3.2 一阶系统的时域分析

3.2一阶系统的时域分析 寒 3)单位脉冲响应 当()=δ()时,系统的输出响应为该系统的脉冲响 应。因为[δ()]=1,一阶系统脉冲响应的拉氏变换为: YS=Φ60F+11=,+令 对应单位脉冲响应为: 2023年7月24日4时48分 北京科技大学自功化学院自功化系 22
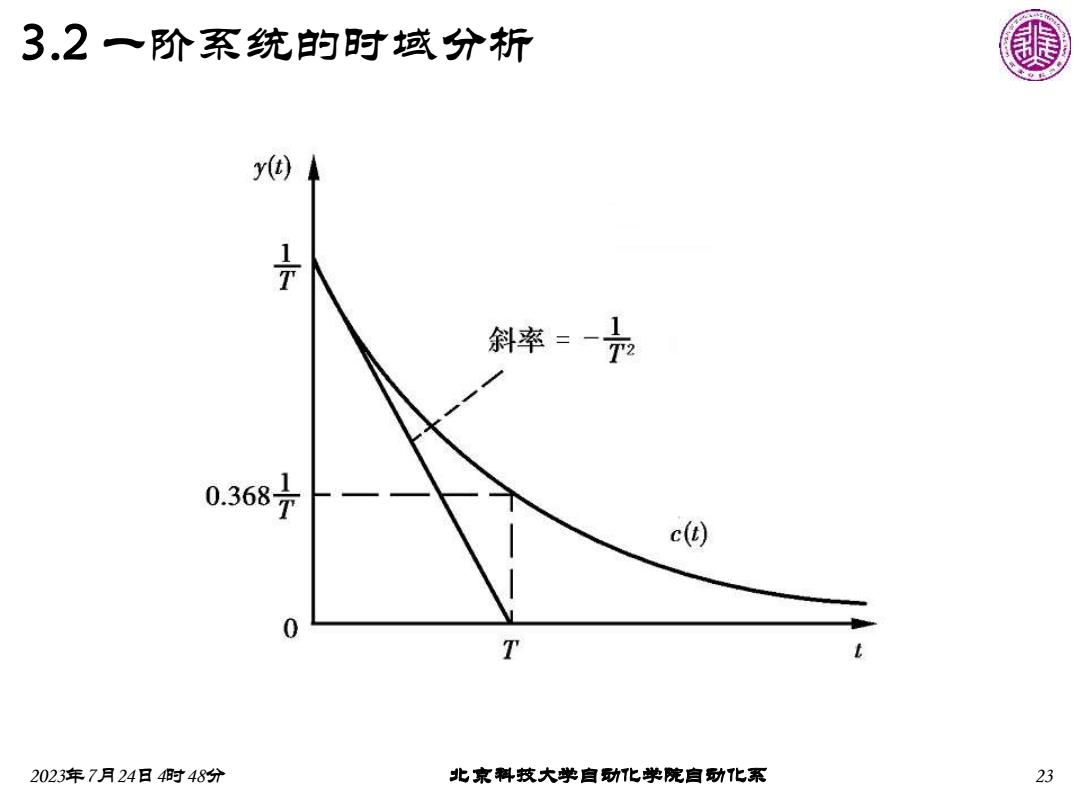
2023年7月24日4时48分 北京科技大学自动化学院自动化系 22 3.2 一阶系统的时域分析 当u(t)=δ(t)时,系统的输出响应为该系统的脉冲响 应。因为L [δ(t)]=1,一阶系统脉冲响应的拉氏变换为: 3)单位脉冲响应 1 1 ( ) ( ) ( ) 1 1 1 T Y s s U s Ts s T = = = + + 1( ) 1 ( ) e t T y t T t = − 对应单位脉冲响应为:
3.2一阶系统的时域分析 y(t) 子 斜率= 0.3687 c(t) 0 T 2023年7月24日4时48分 北京料技大学自动化学院自功化系 23
2023年7月24日4时48分 北京科技大学自动化学院自动化系 23 3.2 一阶系统的时域分析

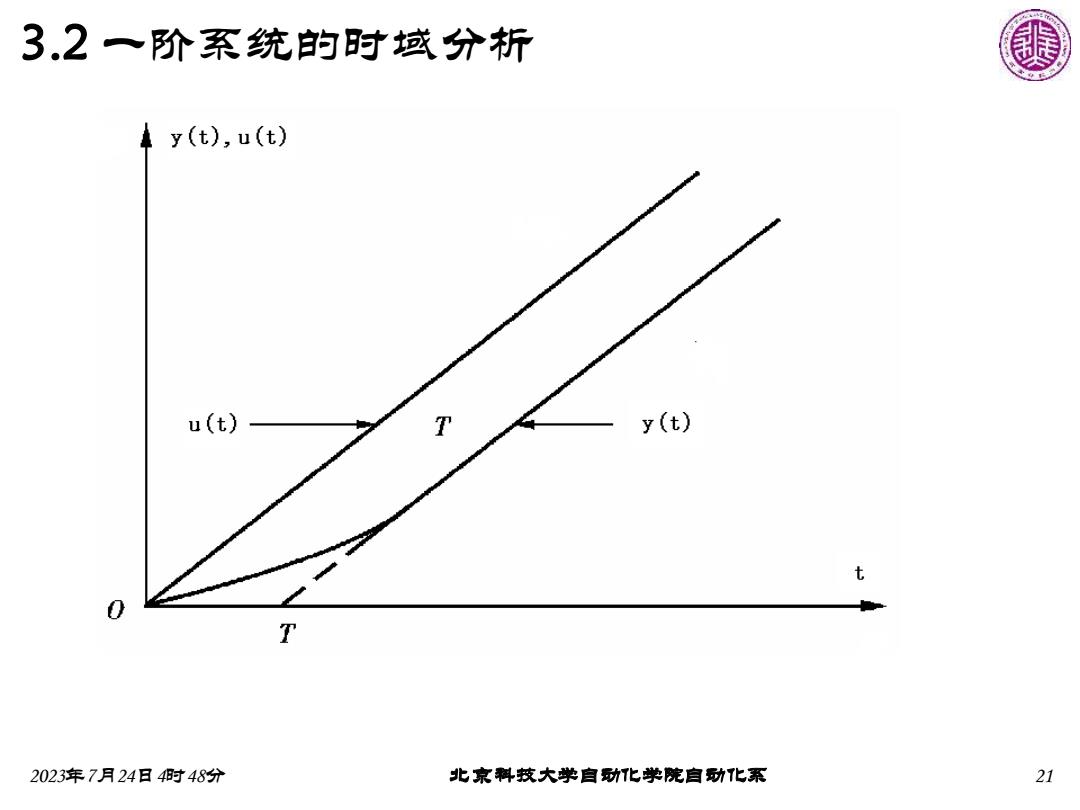
3.2一阶系统的时域分析 u(t) y(t) 若输入函数成导 数关系,则响应函数 6(t) 成导数关条,由于阶 跃响应的暂态特性较 直观,且又有一定代 1(t) 1-eT.1t) 表性,因此今后以单 位阶跃响应分析暂态 t t-T1-ei)-10) 特性。 1-2 - 2-r+T21-e)-10) 2 2023年7月24日4时48分 北京料技大学自功化学院自功化系 24
2023年7月24日4时48分 北京科技大学自动化学院自动化系 24 3.2 一阶系统的时域分析 u(t) 1(t) 1 e 1(t) T t − − t T(1 e ) 1(t) T t − − − (t) 1( ) 1 e t T T t − 2 2 1 t (1 ) 1( ) 2 1 2 2 t Tt T e t T t − + − − y(t) t 若输入函数成导 数关系,则响应函数 成导数关系,由于阶 跃响应的暂态特性较 直观,且又有一定代 表性,因此今后以单 位阶跃响应分析暂态 特性
一阶条统时城分析 k,T一 Φ(S)=Ts+ 时间常数 无零点的一阶系统 (画图时取k=1,T0.5) k()=+e7 h(t)=1-e-t/ c(t)=t-T+Te-tr r()=δ() r()=1(t) r(t)=t Step Response k0r号 h'(0)=1/T K(0)=T h(T)=0.632h(∞) k'(0)=-1/T2 h(2T)=0.865h(o) h(3T)=0.95h(o) h(4T)=0.982h(o) 2 Tme (sec) 1、3个图各如何求T? 2、调节时间t=? 问 3、r(t)=at时,es=? 4、求导关系? 2023 25
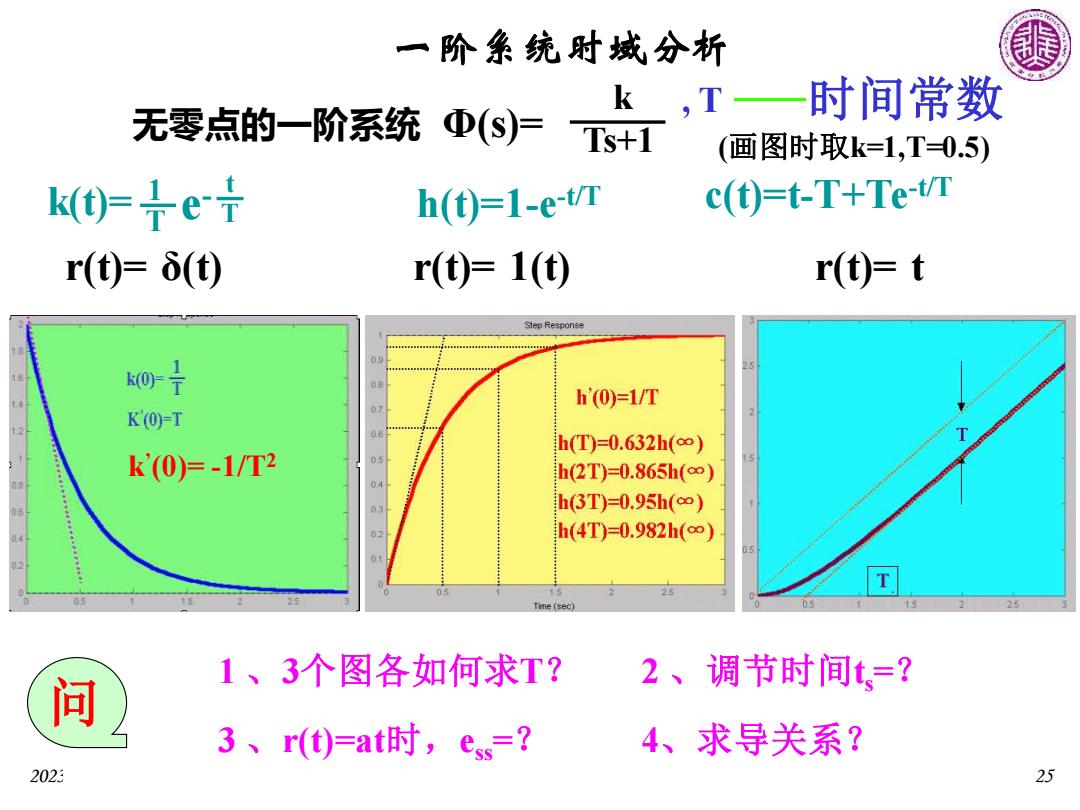
2023年7月24日4时48分 北京科技大学自动化学院自动化系 25 一阶系统时域分析 无零点的一阶系统 Φ(s)= Ts+1 k , T 时间常数 (画图时取k=1,T=0.5) 单 位 脉 冲 响 应 k(t)= T 1 e - T t k(0)= T 1 K’ (0)=T 单 位 阶 跃 响 应 h(t)=1-e -t/T h ’ (0)=1/T h(T)=0.632h(∞) h(3T)=0.95h(∞) h(2T)=0.865h(∞) h(4T)=0.982h(∞) 单 位 斜 坡 响 应 c(t)=t-T+Te-t/T T ? r(t)= δ(t) r(t)= 1(t) r(t)= t 问 1 、3个图各如何求T? 2 、调节时间ts =? 3 、r(t)=at时,ess =? 4、求导关系? k ’ (0)= -1/T2