
3.2一阶系统的时域分析 几点说明和结论: 1°根据动态性能指标的定义, 的暂态指标为: ts=3T(5%)t=4T(2%) 2°如果把复现和跟踪输入信号为理想输出 那么,7 对脉冲和单位阶跃输入时的稳态误差为 0,而对单位斜波输入的稳态误差为T。 3°观察输入信号和对应的输出信号可知,输入函 数成导数关条,则响应函数成导数关系。由于阶跃响 应的暂态特性较直观,且又有一定代表性,因此今后 以单位阶跃响应分析暂态特性。 2023年7月24日4时48分 北京科技大学自功化学院自功化系 26
2023年7月24日4时48分 北京科技大学自动化学院自动化系 26 3.2 一阶系统的时域分析 几点说明和结论: 1 。根据动态性能指标的定义, 的暂态指标为: ts=3T(5%) ts=4T(2%) 2 。 如果把复现和跟踪输入信号为理想输出 那么, 对脉冲和单位阶跃输入时的稳态误差为 0,而对单位斜波输入的稳态误差为T。 3 。观察输入信号和对应的输出信号可知,输入函 数成导数关系,则响应函数成导数关系。由于阶跃响 应的暂态特性较直观,且又有一定代表性,因此今后 以单位阶跃响应分析暂态特性。 1 1 Ts + 1 1 Ts +
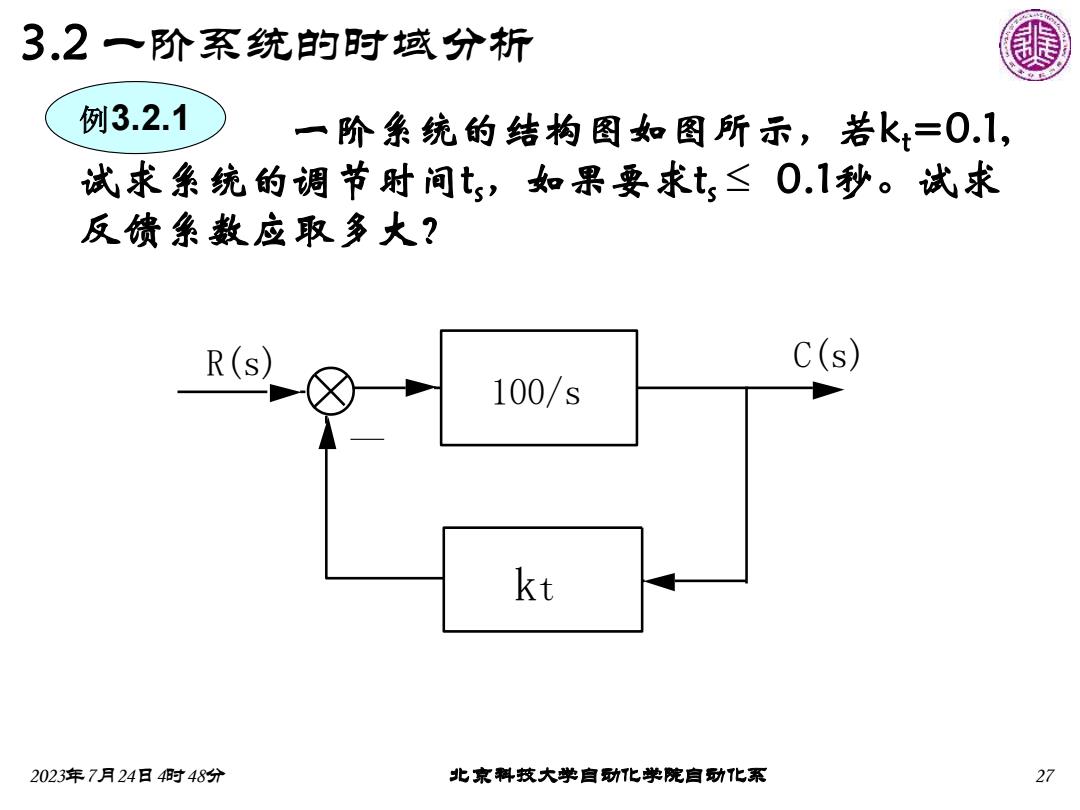
3.2一阶系统的时域分析 例3.2.1 一阶条统的结构图如图所示,若k+=0.1, 试求系统的调节时问t,如果要求t≤0.1秒。试求 反馈象数应取多大? R(s) C(s) 100/s kt 2023年7月24日4时48分 北京料技大学自动化学院自功化系 27
2023年7月24日4时48分 北京科技大学自动化学院自动化系 27 3.2 一阶系统的时域分析 一阶系统的结构图如图所示,若kt=0.1, 试求系统的调节时间ts,如果要求ts 0.1秒。试求 反馈系数应取多大? 100/s kt R(s) C(s) 例3.2.1

3.2一阶系统的时域分析 解 系统的闭环传递函数 100/s 1/k 0.01s +1 当k=0.1时, s)-1+0Xk S k 10 V(s)= 显然时间常数T=0.1秒 0.1s+1 因此调节时间为t。=3T=0.3秒, 如果要求4,≤0.1秒,4,=3T=3 0.01 ≤0.1, k 故k≥0.3 2023年7月24日4时48分 北京料技大学自动化学院自功化系 28
2023年7月24日4时48分 北京科技大学自动化学院自动化系 28 3.2 一阶系统的时域分析 解 系统的闭环传递函数 故kt 0.3 0.1, 0. 01 0.1 , = 3 = 3 t s s k 如果要求 t 秒 t T 因此调节时间为 ts = 3T = 0.3 秒, 显然时间常数 T = 0.1秒 = 0.1 , 当 kt 时 0.1 1 10 ( ) + = s s 1 0. 01 1 / 100 1 100 / ( ) + = + × = t t t k s k k s s s

32一阶系统的时域分析 思考题和选做题: (1)当一阶对象的模型为 k 时,分别求其输出 Ts +1 响应所得的结果是否待合前面的证明和结论?试着 解释为什么有这样的结果? (2)当输入信号为0-财,7+ 的输出响应是 2 什么?能否根据这个结果利用上面思考题直接写出 二1对测式的输出响应? 2023年7月24日4时48分 北京料技大学自动化学院自功化系 ⑤返回 29
2023年7月24日4时48分 北京科技大学自动化学院自动化系 29 3.2 一阶系统的时域分析 思考题和选做题: (1)当一阶对象的模型为 时,分别求其输出 响应所得的结果是否符合前面的证明和结论?试着 解释为什么有这样的结果? (2)当输入信号为 时, 的输出响应是 什么?能否根据这个结果利用上面思考题直接写出 对 的输出响应? Ts +1 k 1 1 Ts + s +1 k 2 2 1 u(t) = t t R t 2 2 1 ( ) =
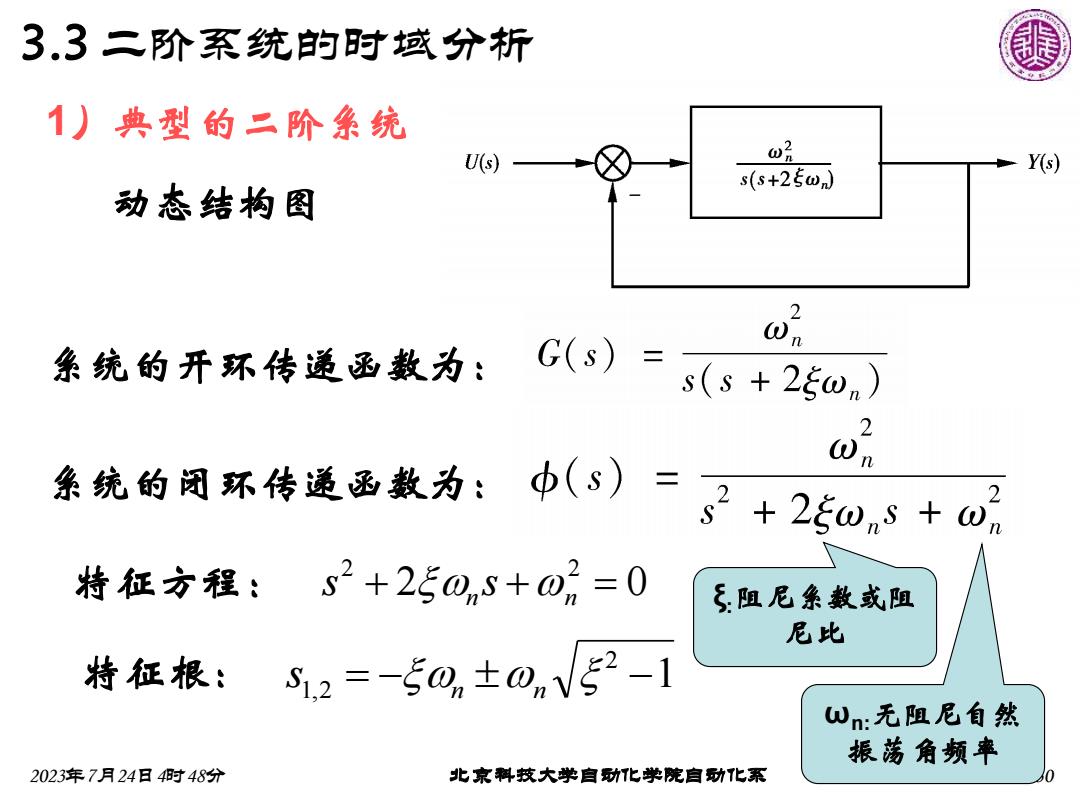
3.3二阶系统的时域分析 1)典型的二阶条统 U(s) ω2 Y(s) s(s+25ω) 动态结构图 2 Wn 系统的开环传递函数为:G(s)= s(s+25wn) 2 象皖的周环传道函教为:b(s)=+2505+0 特征方程:s2+2503+0=0 阻尼条数或阻 尼比 特征根: .2=-50,±0nV52-1 wn:无阻尼自然 振荡角频率 2023年7月24日4时48分 北京料技大学自动化学院自功化系
2023年7月24日4时48分 北京科技大学自动化学院自动化系 30 3.3 二阶系统的时域分析 1)典型的二阶系统 动态结构图 系统的闭环传递函数为: 特征方程: 特征根: 2 0 2 2 s + n s +n = 1 2 s1,2 = − n n − 系统的开环传递函数为: ωn:无阻尼自然 振荡角频率 ξ:阻尼系数或阻 尼比