《概率论与数理统计》课程教学课件（PPT讲稿）第二章 随机变量及其分布 2.3 随机变量的分布函数

第三节 随机变量的分布函数 一、分布函数的概念 二、分布函数的性质 三、例题讲解

一、分布函数的概念 二、分布函数的性质 三、例题讲解 第三节 随机变量的分布函数

一、分布函数的概念 1.概念的引入 对于随机变量X,我们不仅要知道X取哪些值， 要知道X取这些值的概率；而且更重要的是想知 道X在任意有限区间(a,b)内取值的概率. 例如求随机变量X落在区间(，x】内的概率. P{x1<X≤x,HPX≤xPX≤xl F(x2) F 分布函数 P(x]<X<x2}=F(x2)-F(x)

对于随机变量X, 我们不仅要知道X 取哪些值, 要知道 X 取这些值的概率 ; 而且更重要的是想知 道 X 在任意有限区间(a,b)内取值的概率. { } P x1  X  x2 { } { } = P X  x2 − P X  x1 ( ) F x2 ( ) F x1 { } P x1  X  x2 分布函数 ( ) ( ). = F x2 − F x1  ? 一、分布函数的概念 例如 ( , ] . 求随机变量 X 落在区间 x1 x2 内的概率 1.概念的引入

2.分布函数的定义 定义设X是一个随机变量x是任意实数，函数 F(x)=P{X≤x 称为X的分布函数， 说明 ()分布函数主要研究随机变量在某一区间内取值 的概率情况. (2)分布函数F(x)是x的一个普通实函数

2.分布函数的定义 说明 (1) 分布函数主要研究随机变量在某一区间内取值 的概率情况. . ( ) { } , , 称 为 的分布函数 定 义 设 是一个随机变量 是任意实数函 数 X F x P X x X x =  (2)分布函数 F(x) 是 x 的一个普通实函数

实例 抛掷均匀硬币，令 1 出正面， X= 0, 出反面 求随机变量X的分布函数 解X的分布律为 pX=1=pK=0= 0 当x<0时， F(x)=P{X≤x<0}=0;

实例 抛掷均匀硬币, 令    = 0, . 1, , 出反面 出正面 X 求随机变量 X 的分布函数. p{X = 1} = p{X = 0} , 2 1 = • 0 • 1 x 当 x  0时, F(x) = P{X  x  0} = 0; 解 X 的分布律为

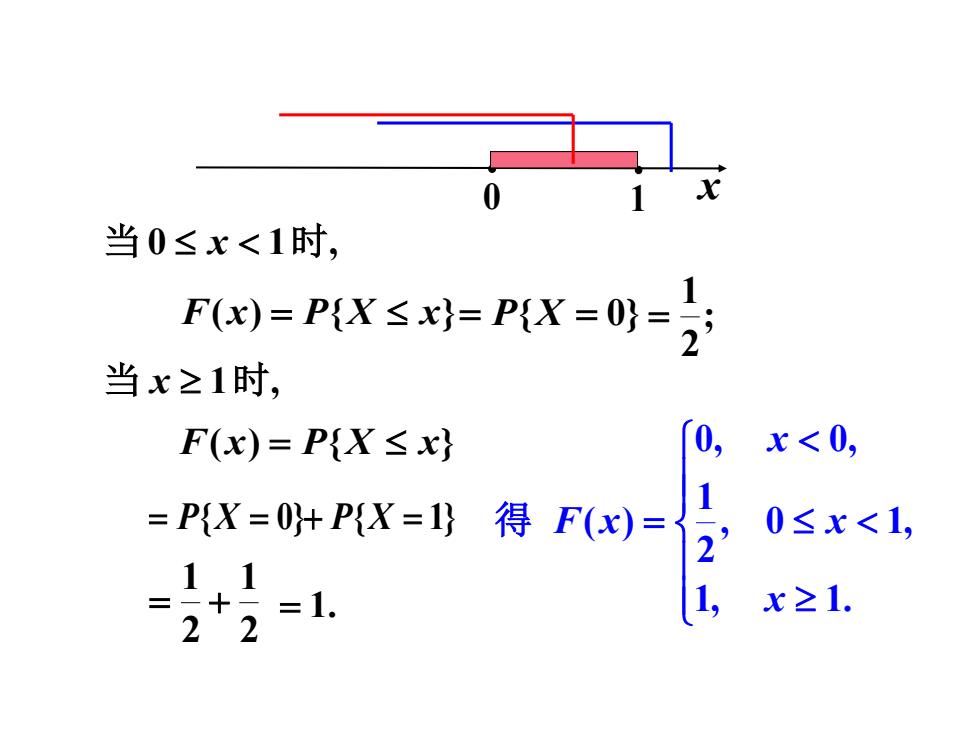
0 当0≤x<1时， Fw)=PX≤=PX=0}= 当x≥1时， F(x)=P{X≤x 0,x<0, =PX=HPK=I)得F9)=) 0≤x<1, 11 22-1. 1, x≥1

• 0 • 1 x 当 0  x  1时, F(x) = P{X  x}= P{X = 0} ; 2 1 = 当 x  1时, F(x) = P{X  x} = P{X = 0}+ P{X = 1} 2 1 2 1 = + = 1.            = 1, 1. , 0 1, 2 1 0, 0, ( ) x x x 得 F x