
概華伦与款程统外 第四章 随机变量的数字特征 分布函数能完整地描述随机变量的统计特 性,但实际应用中并不都需要知道分布函数而 只需知道随机变量的某些特征. 例如: 判断棉花质量时,既看纤维的平均长度 又要看纤维长度与平均长度的偏离程度 平均长度越长,偏离程度越小,质量就越好;
第四章 随机变量的数字特征 分布函数能完整地描述 随机变量的统计特 性, 但实际应用中并不都需要知道分布函数而 只需知道 随机变量的某些特征. 判断棉花质量时, 既看纤维的平均长度 平均长度越长,偏离程度越小, 质量就越好; 又要看 纤维长度与平均长度的偏离程度 例如:

概车伦与散理统外「 考察一射手的水平,既要看他的平均环数是否 高,还要看他弹着点的范围是否小,即数据的波动 是否小. 由上面例子看到,与随机变量有关的某些数 值,虽不能完整地描述随机变量,但能清晰地描 述随机变量在某些方面的重要特征,这些数字特 征在理论和实践上都具有重要意义. 本章主要内容 数学期望、方差、协方差、相关系数、矩
考察一射手的水平, 既要看他的平均环数是否 高, 还要看他弹着点的范围是否小, 即数据的波动 是否小. 由上面例子看到,与随机变量有关的某些数 值,虽不能完整地描述随机变量,但能清晰地描 述随机变量在某些方面的重要特征 ,这些数字特 征在理论和实践上都具有重要意义. 本章主要内容 数学期望、方差、协方差、相关系数、矩

概率伦与款理统外 第一节数学期望 一、数学期望的概念 二、随机变量函数的数学期望 三、数学期望的性质
一、数学期望的概念 三、数学期望的性质 二、随机变量函数的数学期望 第一节 数学期望
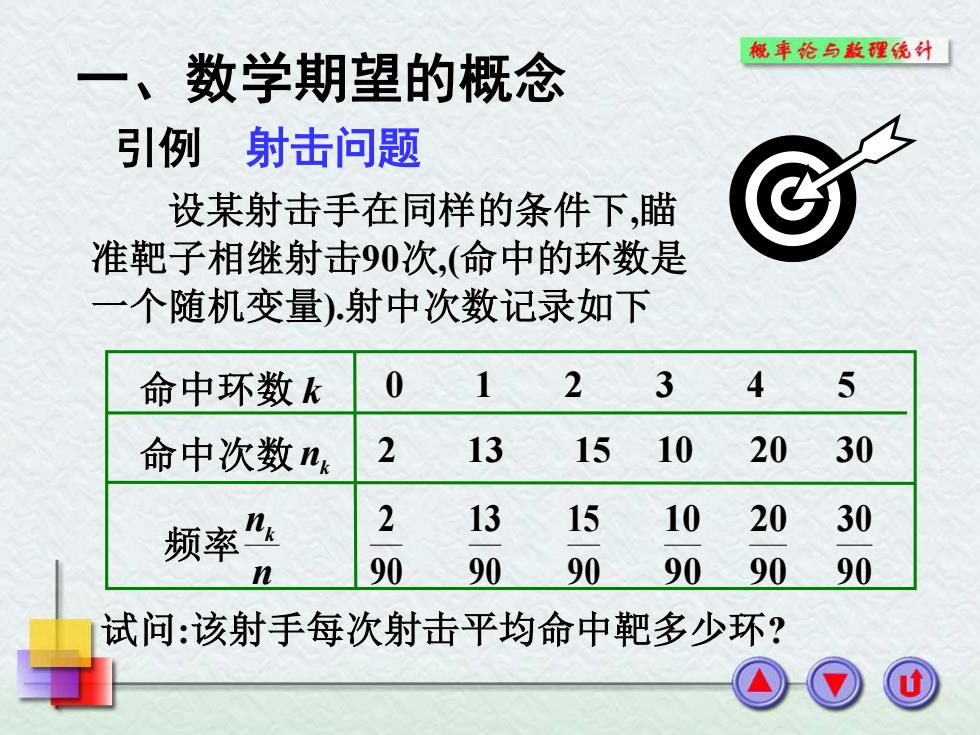
概车纶与款理统外 一、数学期望的概念 引例射击问题 设某射击手在同样的条件下,瞄 准靶子相继射击90次,(命中的环数是 一个随机变量)射中次数记录如下 命中环数k 0 2 3 4 5 命中次数n 2 13 1510 20 30 频率 2 131510 2030 n 90 90 9090 90 90 试问:该射手每次射击平均命中靶多少环?
设某射击手在同样的条件下,瞄 准靶子相继射击90次,(命中的环数是 一个随机变量).射中次数记录如下 引例 射击问题 试问:该射手每次射击平均命中靶多少环? 0 1 2 3 4 5 2 13 15 10 20 30 90 15 90 13 90 2 90 20 90 10 90 30 命中环数 k 命中次数 频率 nk n nk 一、数学期望的概念

概率伦与款程统外 解平均射中环数 射中靶的总环数 射击次数 0×2+1×13+2×15+3×10+4×20+5×30 90 2 13,15 .。10 20 =0× +1× +2× +3× +4× 90 90 90 90 90 30 +5× 90 5 =3.37. k=0 n
解 平均射中环数 射击次数 射中靶的总环数 = 90 0 2 + 113 + 215 + 310 + 4 20 + 5 30 = 90 30 5 90 20 4 90 10 3 90 15 2 90 13 1 90 2 0 + = + + + + = 3.37. = = 5 k 0 k n n k