
智能计算机与应用 2022年7月 Intelligent Computer and Applications Ju.202 文章编号:2095-2163(2022)07-0101-08 中图分类号:TP391.4 文献标志码:A 基于肌肉激活度的关节运动角度分层预测 张文艳,曹乐,阚秀,汪新坤,杨诞 (上海工程技术大学电子电气工程学院,上海201620 摘要:针对表面肌电信号控制假肢手臂大范围关节角度预测精度低的问,本文提出一种基于肌肉激活度的大范围关节运 动角度分层预测。第一层使用误差反向传播网络(BN搭建三分类器,对关节角度进行低、中,高3个级别的初步划分:第 二层使用粒子群(SO)算法对支持向量回归机(SV周)算法自动寻参,并采用3个S0-SVR模型对不同级别的关节角度进行 精确预测。实验结果表明,该种策略下关节角度的预测值与真实值有较高的一致性,角度预测误差不超过7,有助于提高仿 上1 乎关节活动的灵活性 关键词:表面肌电信号:肌肉激话度:关节角度:支持向量回归机 Hierarchical prediction of joint motion angle based on muscle activation ZHANG Wenyan.CAO Le,KAN Xiu.WANG Xinkun.YANG Dan School of Electrical and Electronic Engineering.Shanghai University of Engineering Science.Shanghai 201620.China) medium and high.In the second on PSO)algorithm is used to automatically K that the R n is nomo [Key words]EMG sinal muscle activation:joint angle support ector regression 0引言 学习的方法已经应用于关节角度预测。Clancy使 用非线性动力学模型建立肌电信号和关节力矩的关 肌电控制假肢手臂是利用表面肌电信号 系,相比传统关节力矩估计有了实质性的 (sEMG)作为控制信号的动力式假肢,是一种生物 Parasurama 使用遗传算法(G)估计关节力矩 电信号控制的人机协同系统。肌电控制假肢手臂的 Mohasser和Eklund将快速正交搜索(FOS)应用于 原理为:将上肢残疾者上肢残端肌肉的表面肌电信 关节角度估计,其反映了EMG和关节角度之间的 号转化为假肢动作的控制源信号.进而用假肢手臂 线性关系:Ding和Ham使用神经网络建立sEMG 当失去的手动作。目前对干肌由控制假肢 和关节运动量之间的关系 的研究主要集中在不同肢体动作的 式分类 目前的研究集中于多关节估计和闭环反债,X 对肢体的运动状态,如:用力情况、运动速度、关节角 关节预测范围的研究少之又少。在人机交互的过 度和关节转动幅度的研究较少,但是在仿生假肢手 中,假肢手臂不可避免的要做关节运动范用较大的 臂的实际应用中,仅靠模式分类的结果无法实现假 动作,所以大范围关节角度的预测准确性对于假肢 肢手臂的关节像人的上肢一样灵活。 手臂结确控制至关重要。但角度范围增大不可群免 随者智能机器人技术的不断发展,肌电信号控 的会对角度拟合精度产生较大影响,如何对大范围 制假肢手的关键 题变为使用表面肌电信号实现 关节角度进行精确预测是目前研究的热点和难点 续运动的精确预测,实现假肢手臂像人的手臂一村 基于上述问题,本文提出了连续关节角度分月 灵活动作。针对提高关节灵活性,深度学习和机器 方案来对大范围关节角度进行预测。第一层采用 基金项目:国家白然科学基金(617心 作者简介:张文艳( 6-),女,硕士研究生 ,主要研究方:生物电估号,生物信号采集与据分标: 乐(1986-),男,博士,讲师,顾士生导 师,主要研 问:惯性传感鉴偏性导航定位微锅合号检测技术 通讯作者:育乐 ca06002延16.0 收稿日期:2021-10-2 心尔次工业大学主办学术研完占应用 C)1994-2022 China Academic Journal Electronic Publishing House.All rights reserved. http://www.cnki.ne
第 12 卷 第 7 期 Vol.12 No.7 智 能 计 算 机 与 应 用 Intelligent Computer and Applications 2022 年 7 月 Jul. 2022 文章编号: 2095-2163( 2022) 07-0101-08 中图分类号: TP 391.4 文献标志码: A 基于肌肉激活度的关节运动角度分层预测 张文艳,曹 乐,阚 秀,汪新坤,杨 诞 ( 上海工程技术大学 电子电气工程学院,上海 201620) 摘 要: 针对表面肌电信号控制假肢手臂大范围关节角度预测精度低的问题,本文提出一种基于肌肉激活度的大范围关节运 动角度分层预测。第一层使用误差反向传播网络( BPNN) 搭建三分类器,对关节角度进行低、中、高 3 个级别的初步划分; 第 二层使用粒子群( PSO) 算法对支持向量回归机( SVR) 算法自动寻参,并采用 3 个 PSO-SVR 模型对不同级别的关节角度进行 精确预测。实验结果表明,该种策略下关节角度的预测值与真实值有较高的一致性,角度预测误差不超过 7°,有助于提高仿 生假肢手臂关节活动的灵活性。 关键词: 表面肌电信号; 肌肉激活度; 关节角度; 支持向量回归机 Hierarchical prediction of joint motion angle based on muscle activation ZHANG Wenyan,CAO Le,KAN Xiu,WANG Xinkun,YANG Dan ( School of Electrical and Electronic Engineering,Shanghai University of Engineering Science,Shanghai 201620,China) 【Abstract】Aiming at the low accuracy of large-scale joint angle prediction of EMG controlled prosthetic arm,a hierarchical prediction of large-scale joint angle based on muscle activation is proposed. The first layer uses the error back propagation network ( BPNN) to build three classifiers to preliminarily divide the joint angle into three levels: low,medium and high. In the second layer,particle swarm optimization ( PSO) algorithm is used to automatically seek parameters of support vector regression ( SVR) algorithm,and three PSO-SVR models are used to accurately predict joint angles at different levels. The experimental results show that the predicted value of joint angle under this strategy is consistent with the real value,and the angle prediction error is no more than 7 degrees,which is helpful to improve the flexibility of joint movement of bionic prosthetic arm. 【Key words】surface EMG signal; muscle activation; joint angle; support vector regression 哈尔滨工业大学主办 ◆学术研究与应用 基金项目: 国家自然科学基金( 61703270) 。 作者简介: 张文艳( 1996-) ,女,硕士研究生,主要研究方向: 生物电信号、生物信号采集与数据分析; 曹 乐( 1986-) ,男,博士,讲师,硕士生导 师,主要研究方向: 惯性传感器、惯性导航定位、微弱信号检测技术。 通讯作者: 曹 乐 Email: caole00012@ 163.com 收稿日期: 2021-10-26 0 引 言 肌电 控 制 假 肢 手 臂 是 利 用 表 面肌电信号 ( sEMG) 作为控制信号的动力式假肢,是一种生物 电信号控制的人机协同系统。肌电控制假肢手臂的 原理为: 将上肢残疾者上肢残端肌肉的表面肌电信 号转化为假肢动作的控制源信号,进而用假肢手臂 充当失去的手臂动作。目前对于肌电控制假肢手臂 的研究主要集中在不同肢体动作的模式分类[1]。 对肢体的运动状态,如: 用力情况、运动速度、关节角 度和关节转动幅度的研究较少,但是在仿生假肢手 臂的实际应用中,仅靠模式分类的结果无法实现假 肢手臂的关节像人的上肢一样灵活。 随着智能机器人技术的不断发展,肌电信号控 制假肢手的关键问题变为使用表面肌电信号实现连 续运动的精确预测,实现假肢手臂像人的手臂一样 灵活动作。针对提高关节灵活性,深度学习和机器 学习的方法已经应用于关节角度预测。Clancy [2]使 用非线性动力学模型建立肌电信号和关节力矩的关 系,相比传统关节力矩估计有了实质性的改善; Parasuraman [3]使用遗传算法( GA) 估计关节力矩; Mobasser 和 Eklund [4]将快速正交搜索( FOS) 应用于 关节角度估计,其反映了 sEMG 和关节角度之间的 线性关系; Ding 和 Han [5]使用神经网络建立 sEMG 和关节运动量之间的关系。 目前的研究集中于多关节估计和闭环反馈,对 关节预测范围的研究少之又少。在人机交互的过程 中,假肢手臂不可避免的要做关节运动范围较大的 动作,所以大范围关节角度的预测准确性对于假肢 手臂精确控制至关重要。但角度范围增大不可避免 的会对角度拟合精度产生较大影响,如何对大范围 关节角度进行精确预测是目前研究的热点和难点。 基于上述问题,本文提出了连续关节角度分层 方案来对大范围关节角度进行预测。第一层采用

102 智能计算机与应用 第12卷 BPNN算法构建分类器,将大范围关节角度划分为3 文提出基于肌肉激活度的分层预测方案,如图1所 个等级的小范围关节信号:第二层使用SVR模型 示。首先,采集尺侧腕屈肌、桡侧腕屈肌、桡侧长腕 使用PS0算法对其中高斯核函数和松弛变量自动 伸肌和指伸肌的表面肌电信号,并将采集到的表面 寻参,对小范围关节角度进行精确预测。此方案实 肌申信号讲行预处理:其次,对处理过的表面肌申信 现了对大范围关节角度的精确预测 号计算肌肉激活度,使用B即NN分层算法将大范围 1系统框架 角度划分为3个小范围角度:最后,使用3个PS0- SVR模型对关节角度进行准确预测。 针对上肢关节角度预测准确率不高的问题,本 该方案适用于大范围关节角度动态预测,结合 肌电信号进行降噪处理的原理为:通过丢弃高斯白 深度学习和机器学习算法,其复杂性低、处理快速 声(WGN)(m来抑制信号s(中的噪声部分 参数少且提取特征值较少,将粒子群算法用于模型 并恢复去噪后的信号凡),基本模型表示为公 参数寻优,避免了人工调参耗时长、不准确的缺点。 式(1)。 s(n)=An)+e(n) (1 2信号处理 本文选用4小波进行5层分解,如图2所示 2.1信号预处理 首先,通过执行小波变换分解原始信号:其次,对符 本文使用小波变换的方法进行表面肌电信号的 到的细节系数应用适合的阅值,并将所有系数归( 降噪处理。小波变换对信号的时频域特征同时进行 到其相关阈值之下:最后,基于修改后的细节系数重 局部分析,其特点为分辨率分析。小波变换法对 构去噪后的表面肌电信号。 0 选择分解函数 计算阅货 重构去噪后的信号 留2基于小液变换的肌电信号去保 Fig.2 Deno sing of EMG signal based on Wavelet Transfor 对去噪后的表面肌电信号,首先使用截止频率 流,将信号取绝对值:最后,将全波整流后的信号通 为30Hz的四阶巴斯特沃(butter))高通滤波器去除 过四阶巴斯特沃低通滤波器,截止频率为5Hz,用 运动伪迹:其次,对去除运动伪迹的信号进行全波整 干描拟肌肉低波翠特性。表面肌由信号预处理 (C)1994-2022 China Academie Joumal Eleetronie Publishing House.All rights reserved.http://www.enki.net
BPNN 算法构建分类器,将大范围关节角度划分为 3 个等级的小范围关节信号; 第二层使用 SVR 模型, 使用 PSO 算法对其中高斯核函数和松弛变量自动 寻参,对小范围关节角度进行精确预测。此方案实 现了对大范围关节角度的精确预测。 1 系统框架 针对上肢关节角度预测准确率不高的问题,本 文提出基于肌肉激活度的分层预测方案,如图 1 所 示。首先,采集尺侧腕屈肌、桡侧腕屈肌、桡侧长腕 伸肌和指伸肌的表面肌电信号,并将采集到的表面 肌电信号进行预处理; 其次,对处理过的表面肌电信 号计算肌肉激活度,使用 BPNN 分层算法将大范围 角度划分为 3 个小范围角度; 最后,使用 3 个 PSO- SVR 模型对关节角度进行准确预测。 角 度 预 测 结 果 分 析 三 分 类 B P N N 算 法 计 算 肌 肉 激 活 度 PSO 高级SVR模型 中级SVR模型 低级SVR模型 预处理 和降噪 力信号 sEMG 图 1 基于肌肉激活度的分层预测方案 Fig. 1 Hierarchical prediction scheme based on muscle activation 该方案适用于大范围关节角度动态预测,结合 深度学习和机器学习算法,其复杂性低、处理快速、 参数少且提取特征值较少,将粒子群算法用于模型 参数寻优,避免了人工调参耗时长、不准确的缺点。 2 信号处理 2.1 信号预处理 本文使用小波变换的方法进行表面肌电信号的 降噪处理。小波变换对信号的时频域特征同时进行 局部分析,其特点为分辨率分析[6]。小波变换法对 肌电信号进行降噪处理的原理为: 通过丢弃高斯白 噪声( WGN) e( n) 来抑制信号 s( n) 中的噪声部分, 并恢复 去 噪 后 的 信 号 f( n) ,基本模型表示为公 式( 1) 。 s( n) = f( n) + e( n) ( 1) 本文选用 db4 小波进行 5 层分解,如图 2 所示。 首先,通过执行小波变换分解原始信号; 其次,对得 到的细节系数应用适合的阈值,并将所有系数归 0 到其相关阈值之下; 最后,基于修改后的细节系数重 构去噪后的表面肌电信号。 200-20-400 -0.5 -1.0 -1.5 1 0 -1 20-2 100-10-2020 0 -2020 0 -20 s a5 d5 d4 d2 d1 d3 d5 d4 d2 d1 d3 Decompositionatlennt5:s=a5+d5+d4+d3+d2+d1 Originaldetailscoefficients 5 0 -5 10 0 -10 40200-20-40 40 20 0-20 -40 20 0-20 2000 4000 6000 8000 10000 200040006000800010000 200040006000800010000 5 4 3 2 1 5 4 3 2 L1evelnumber Levelnumber Criginalcoefficients Thresholdedcoefficients Originalandde-noisedsignals 20 0 -20 -40 200040006000800010000 1000200030004000500060007000800090001000011000 选择分解函数 计算阈值 重构去噪后的信号 图 2 基于小波变换的肌电信号去噪 Fig. 2 Denoising of EMG signal based on Wavelet Transform 对去噪后的表面肌电信号,首先使用截止频率 为 30 Hz 的四阶巴斯特沃( butter) 高通滤波器去除 运动伪迹; 其次,对去除运动伪迹的信号进行全波整 流,将信号取绝对值; 最后,将全波整流后的信号通 过四阶巴斯特沃低通滤波器,截止频率为 5 Hz,用 于模拟肌肉低通滤波器特性。表面肌电信号预处理 102 智 能 计 算 机 与 应 用 第 12 卷
第7期 张文艳,等:基于肌肉激活度的关节运动角度分层预测 步骤如图3所示。 A2=L,*L2 (3) a4a☒ 8=A,+λ,+1.0 b(t)=s*ad(t-d)b(t-1)-Ab(t-2) 预处理后信号金流整被30高通 (5 这是一个递归模型,单次的神经激活度 图3预处理步骤 Fig.3 Pretreatment steps 和前两次的神经激活度b(t-1)、入,b(t-2)有关 2.2肌肉激活度 入1=0.5,入2=0.5。 建立非线性模型,根据神经激活度Mt)求解肌 将采集到的手部力信号的最大值视为100%肌 肉激活度的信号,最大值定义为MVC,将处理过的 肉激活度(),肌肉激活模型如公式(6) 肌电信号除以MVC,得到归 北后的信号a() 1)e-1 其中,C是非线性形状系数,代表肌肉激活强 利用信号()建立神经激活模型,求解神经溜 活府b),信号a(t)的长度为1,i的取值为1:1. 度c()和神经激活强度b()的非线性程度,C的 取值为-1.5,)为计算出的肌肉激活强度。左手 入,、入,为递归系数,£为增益系数,d为电极廷迟时 间,该模型如公式(2)~公式(5): 和右手尺侧腕屈肌、桡侧腕屈肌、桡侧长腕伸肌和指 (2) 伸肌的肌肉激活度如 图4所示 入,=L,支园 15 20 1.5 2.0 0 20x1 20d :w 05 20 0.5 1.0 15 0.5 1.0 0 10 20 10 图4肌肉激活度 Fig.4 Muscle ac 没有得到期望输出,就会进入反向传播过程,根据逻 3关节角度分层预测算法 差信号调整网络各层的权值和阑值,使BPNN的实 为了能够对大范围关节角度做到精准预测.使 际输出不断接近期望输出,如图5所示。 用BPNN算法将大范围关节角度划分为小范围关节 1● 角度。BPNN算法将大范围关节角度进行三分类 分别为0°-30°,31°-60°,61°-90°,建立3个SVR 模型对小范围关节角度预测。 3.1BPNN算法 隐含尿 BPNN是一种信号前向传播,误差反向传播的 ,围5BPN结构图 多层前馈神经网络 。在信号前向传播中,施加 B即N在预测输出之前要进行网络训练.会产生 输入信号从输入层X向前传播经过隐含层处理,肖 记忆和预测能力。隐含层输出M通过公式(7)计算。 到输出层Y输出信号。每一层神经元的状态只会 影响其连接的下一层神经元状态。如果输出层Y M=∑(0g:-).j=1.2.1(7列 C)1994-2022 China Academie Jourmal Eleetronie Publishing House All rights reserved. http://www.cnki.net
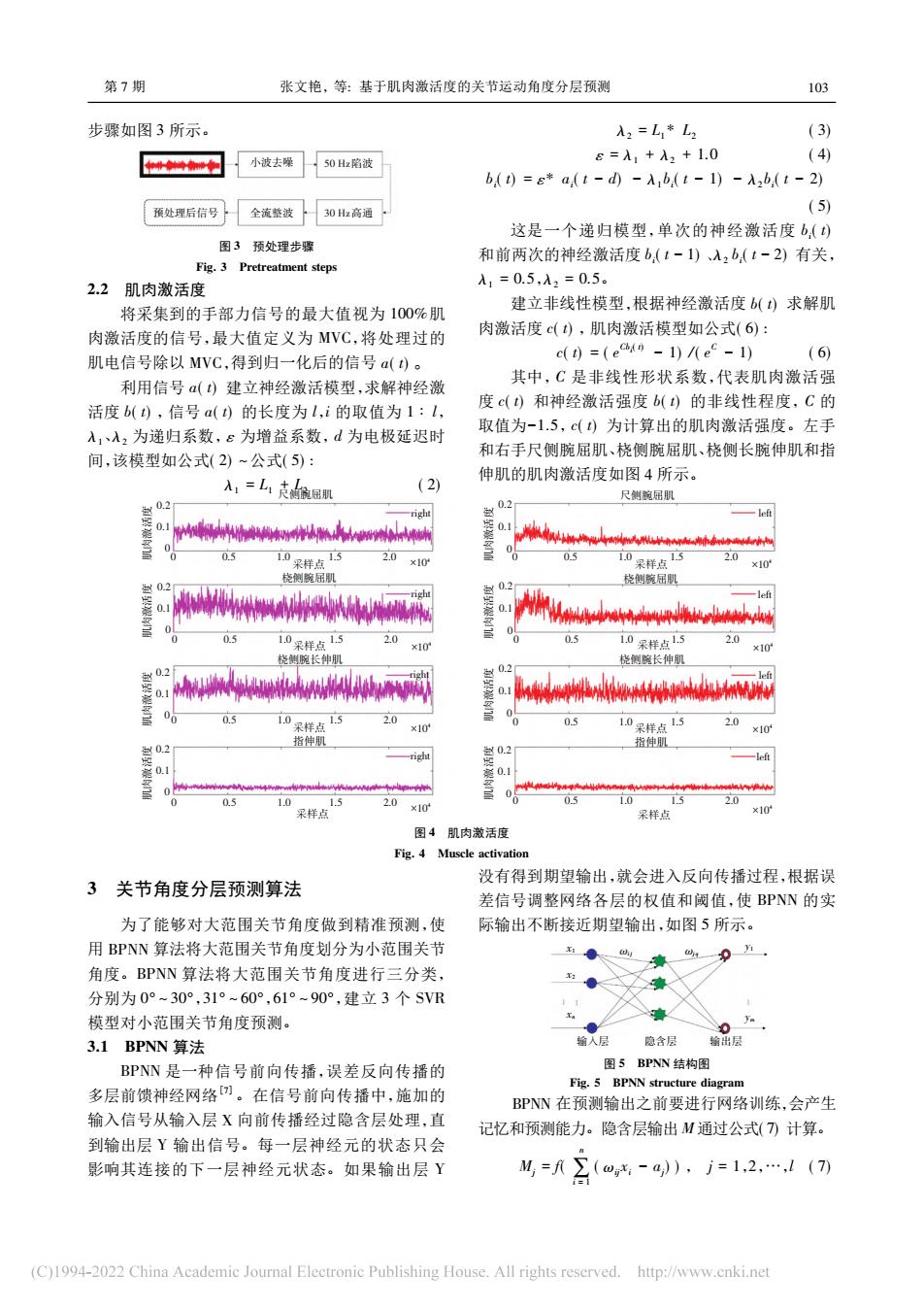
步骤如图 3 所示。 预处理后信号 小波去噪 全流整波 50Hz陷波 30Hz高通 图 3 预处理步骤 Fig. 3 Pretreatment steps 2.2 肌肉激活度 将采集到的手部力信号的最大值视为 100%肌 肉激活度的信号,最大值定义为 MVC,将处理过的 肌电信号除以 MVC,得到归一化后的信号 a( t) 。 利用信号 a( t) 建立神经激活模型,求解神经激 活度 b( t) ,信号 a( t) 的长度为 l,i 的取值为 1 ∶ l, λ1、λ2 为递归系数,ε 为增益系数,d 为电极延迟时 间,该模型如公式( 2) ~公式( 5) : λ1 = L1 + L2 ( 2) λ2 = L1 * L2 ( 3) ε = λ1 + λ2 + 1.0 ( 4) bi ( t) = ε* ai ( t - d) - λ1 bi ( t - 1) - λ2 bi ( t - 2) ( 5) 这是一个递归模型,单次的神经激活度 bi ( t) 和前两次的神经激活度 bi ( t - 1) 、λ2 bi ( t - 2) 有关, λ1 = 0.5,λ2 = 0.5。 建立非线性模型,根据神经激活度 b( t) 求解肌 肉激活度 c( t) ,肌肉激活模型如公式( 6) : c( t) = ( e Cbi ( t) - 1) /( e C - 1) ( 6) 其中,C 是非线性形状系数,代表肌肉激活强 度 c( t) 和神经激活强度 b( t) 的非线性程度,C 的 取值为-1.5,c( t) 为计算出的肌肉激活强度。左手 和右手尺侧腕屈肌、桡侧腕屈肌、桡侧长腕伸肌和指 伸肌的肌肉激活度如图 4 所示。 0 0.5 1.0 1.5 2.0 采样点 0.2 0.1 0 肌 肉 激 活 度 right 尺侧腕屈肌 ×104 0.2 0.1 肌 0 肉 激 活 度 0.2 0.1 0 肌 肉 激 活 度 0.2 0.1 肌 0 肉 激 活 度 right right right 0 0.5 1.0 1.5 2.0 采样点 ×104 0 0.5 1.0 1.5 2.0 采样点 ×104 0 0.5 1.0 1.5 2.0 采样点 ×104 桡侧腕屈肌 桡侧腕长伸肌 指伸肌 0 0.5 1.0 1.5 2.0 采样点 0.2 0.1 0 肌 肉 激 活 度 left 尺侧腕屈肌 ×104 0.2 0.1 肌 0 肉 激 活 度 0.2 0.1 0 肌 肉 激 活 度 0.2 0.1 肌 0 肉 激 活 度 left left left 0 0.5 1.0 1.5 2.0 采样点 ×104 0 0.5 1.0 1.5 2.0 采样点 ×104 0 0.5 1.0 1.5 2.0 采样点 ×104 桡侧腕屈肌 桡侧腕长伸肌 指伸肌 图 4 肌肉激活度 Fig. 4 Muscle activation 3 关节角度分层预测算法 为了能够对大范围关节角度做到精准预测,使 用 BPNN 算法将大范围关节角度划分为小范围关节 角度。BPNN 算法将大范围关节角度进行三分类, 分别为 0° ~ 30°,31° ~ 60°,61° ~ 90°,建立 3 个 SVR 模型对小范围关节角度预测。 3.1 BPNN 算法 BPNN 是一种信号前向传播,误差反向传播的 多层前馈神经网络[7]。在信号前向传播中,施加的 输入信号从输入层 X 向前传播经过隐含层处理,直 到输出层 Y 输出信号。每一层神经元的状态只会 影响其连接的下一层神经元状态。如果输出层 Y 没有得到期望输出,就会进入反向传播过程,根据误 差信号调整网络各层的权值和阈值,使 BPNN 的实 际输出不断接近期望输出,如图 5 所示。 x1 x2 xn ωij y1 ym ωjq 输入层 隐含层 输出层 图 5 BPNN 结构图 Fig. 5 BPNN structure diagram BPNN 在预测输出之前要进行网络训练,会产生 记忆和预测能力。隐含层输出 M 通过公式( 7) 计算。 Mj = f( ∑ n i = 1 ( ωij xi - aj ) ) , j = 1,2,.,l ( 7) 第 7 期 张文艳,等: 基于肌肉激活度的关节运动角度分层预测 103

104 智能计算机与应用 第12卷 其中,a为隐含层阀值:l为隐含层节点数:n为 网络连接权值,和仙。更新的计算为公式 输入节点数::为输入层和隐含层之间的连接权 (11)和公式(12): 值:x为输入变量;∫为隐含层激励函数。本文所选 的激励函数如公式(8): ,=+n以1-)0,emo 1 i=1,2,.,mj=1,2,.,l(11 1+e (8 wn=n+nlM,errof,广=1,2,.,kg=1,2,.,m BPNN的预测输出N计算公式(9): (12 其中,n为输入层节点数,n为学习速率。 N,=∑M,wn-b,9=1,2,.,m(9列 根据预测误差eror更新隐含层节点阅值a和输 其中,m为输出节点数:b为输出层阀值:0为 出层节点阀值b的计算公式为公式(13)和公式14: 隐含层和输出层的连接权值;M为隐含层输出。 络预测误差的计算如公式(10) =g+n1-9∑em,j=1,2.1(13 ero1=Y。-N。,g=1,2,.,m (10 9=12,.,m (14) 其中,Y,为期望输出:N,为网络预测输出: error为网络预测误差」 表1BPNN训炼过程 Tab.1 BPNN training proces 网络训练步 .确定学习速半和神经元微切函数: 根公式(2史新树路连接权值,和 BPNN搭建根据系统输入输出数据的特点确定 映射到高维线性特征空间,并利用原始空间的核函 其结构,由于以肌肉激活度为输入信号的维数为8】 数代替高维空间的点积运算,最终构造变量的拟合 待分类的角度信号共有3类,所以搭建的B即神经 函救。假设救据样本空间为【(x,¥,),.,x 国路给入层为8个带占,给出层为3个节占。BN )】CN×R,其中,x为输入:Y为输出:n为训练 的隐含层节点数会影响网络的分类准确率,隐含层 样本数:N为训练样本空间。 节点数太少 成网络学习不充 ,影响分类精度 SVR的研究目的是用一个函数来表示x和y之 隐含层节点数太多会增加训练时间造成过拟合,隐 间的关系,即对于给定的x可以通过函数来预测相 含层节点数1的选择如公式(15): 应的y值。本文构造的拟合函数如公式(16): =los.n 15 fx)=(x)+b 16 其中,为隐含层节点数:n为输入层节点数 其中,w为法向量:b为截距:sx为x的非线 输出层节点数 为 1 之间的常数 性映射,当x和y之间的关系为非线性时 3.2 PSO-SVR算法 以将x映射到 个新的空间 在公式(13)中确 本文使用SVR算法对小范围关节角度进行精 回归系数ω和,这个问题可以转化为一个凸优化 确预测。为讲行小范围预测,训练3个SVR模型即 问题,计算如公式(17): 0°30°、31°w60°和61°一90°,且则练数据对应的关 节角度宽用与BPNN相同。SVB刑中右需男手 目标函数:min2·+C(∑5+£】 动确定参数 、工调参需要大 的先 ·(刘-b≤+专 易造成训练模型结果不佳。为了解决人工调参的缺 约束条件: w(x)+b-y≤E+E (17 点,本文引入PS0算法自动寻优SVR模型参数。 E,≥0 3.2.1SVR模型原理及训练 其中,为松弛因子:()为非线性映射 SVR是一种拟合算法,通过非线性变换将样木 函数:C为惩罚系数:s为函数的拟合精度】 C)1994-2022 China Academie Joumal Eleetronie Publishing House.All rights reserved.http://www.enki.net
其中,a 为隐含层阈值; l 为隐含层节点数; n 为 输入节点数; ωij 为输入层和隐含层之间的连接权 值; x 为输入变量; f 为隐含层激励函数。本文所选 的激励函数如公式( 8) : f( x) = 1 1 + e -x ( 8) BPNN 的预测输出 N 计算公式( 9) : Nq = ∑ l j = 1 Mjωjq - bq, q = 1,2,.,m ( 9) 其中,m 为输出节点数; b 为输出层阈值; ωjq 为 隐含层和输出层的连接权值; M 为隐含层输出。网 络预测误差的计算如公式( 10) : errork = Yq - Nq, q = 1,2,.,m ( 10) 其中,Yq 为期望输出; Nq 为网络预测输出; error 为网络预测误差。 网络 连 接 权 值 ωij 和 ωjq 更 新 的 计 算 为 公 式 ( 11) 和公式( 12) : ωij = ωij + ηMj ( 1 - Mj ) x( i) ∑ m k = 1 ωjq errork, i = 1,2,.,n; j = 1,2,.,l ( 11) ωjq = ωjq + ηMj errork, j = 1,2,.,l; q = 1,2,.,m ( 12) 其中,n 为输入层节点数,η 为学习速率。 根据预测误差 error 更新隐含层节点阈值 a 和输 出层节点阈值 b 的计算公式为公式( 13) 和公式( 14) : aj = aj + ηMj ( 1 - Mj )∑ m k = 1 ωjq errork,j = 1,2,.,l ( 13) bq = bq + errork, q = 1,2,.,m ( 14) BPNN 网络的训练过程,见表 1。 表 1 BPNN 训练过程 Tab. 1 BPNN training process 网络训练步骤 Step1: 初始化网络,根据数据特征确定 n、l、m、ωij、ωjq、a、b,确定学习速率 η 和神经元激励函数; Step2: 根据公式( 7) 和公式( 8) 计算隐含层输出 M; Step3: 根据公式( 9) 计算输出层输出 N; Step4: 根据公式( 10) 计算网络预测误差 error; Step5: 根据公式( 11) ( 12) 更新网络连接权值 ωij 和 ωjq ; Step6: 根据公式( 13) ( 14) 更新网络节点阈值 a 和 b; Step7: 判断算法迭代是否结束,若没有结束,返回 Step2。 BPNN 搭建根据系统输入输出数据的特点确定 其结构,由于以肌肉激活度为输入信号的维数为 8, 待分类的角度信号共有 3 类,所以搭建的 BP 神经 网络输入层为 8 个节点,输出层为 3 个节点。BPNN 的隐含层节点数会影响网络的分类准确率,隐含层 节点数太少会造成网络学习不充分,影响分类精度; 隐含层节点数太多会增加训练时间造成过拟合。隐 含层节点数 l 的选择如公式( 15) : l = log2 n ( 15) 其中,l 为隐含层节点数; n 为输入层节点数; m 为输出层节点数; s 为 0~10 之间的常数。 3.2 PSO-SVR 算法 本文使用 SVR 算法对小范围关节角度进行精 确预测。为进行小范围预测,训练 3 个 SVR 模型即 0° ~30°、31° ~60°和 61° ~ 90°,且训练数据对应的关 节角度范围与 BPNN 相同。SVR 模型中有需要手 动确定参数,但是人工调参需要大量的先验经验,容 易造成训练模型结果不佳。为了解决人工调参的缺 点,本文引入 PSO 算法自动寻优 SVR 模型参数。 3.2.1 SVR 模型原理及训练 SVR 是一种拟合算法,通过非线性变换将样本 映射到高维线性特征空间,并利用原始空间的核函 数代替高维空间的点积运算,最终构造变量的拟合 函数[8]。假设数据样本空间为 { ( x1,y1 ) ,.,( xn, yn ) } ⊂ N × R,其中,x 为输入; y 为输出; n 为训练 样本数; N 为训练样本空间。 SVR 的研究目的是用一个函数来表示 x 和 y 之 间的关系,即对于给定的 x 可以通过函数来预测相 应的 y 值。本文构造的拟合函数如公式( 16) : f( x) = ωφ( x) + b ( 16) 其中,ω 为法向量; b 为截距; φ( x) 为 x 的非线 性映射,当 x 和 y 之间的关系为非线性时,φ( x) 可 以将 x 映射到一个新的空间。在公式( 13) 中确定 回归系数 ω 和 b ,这个问题可以转化为一个凸优化 问题,计算如公式( 17) : 目标函数: min 1 2 ( ω·ω) + C( ∑ l i = 1 ξ + ξ * ) 约束条件: y - ω·φ( x) - b ≤ ε + ξ ωφ( x) + b - y ≤ ε + ξ * ξ,ξ * ≥ 0 { ( 17) 其中,ξ、ξ * 为松弛因子; φ( x) 为非线性映射 函数; C 为惩罚系数; ε 为函数的拟合精度。 104 智 能 计 算 机 与 应 用 第 12 卷

第7期 张文艳,等:基于肌肉激活度的关节运动角度分层预测 105 引入拉格朗日乘子a,m:和n”,相应的 使用PS0算法选取参数来改进SVR模型。PS0是 格朗日方程为公式(18) 种基于种群的随机搜索算法,用于解决无约束伊 4ws)=31u2+c(+)- 化问颗。在粒子生成过程中,粒子根据自身的经 验以及相邻粒子的经验改变其位置。PS0系统将局 a(e+-%+(到+) 部搜索方法与全局搜索策略相结合,以达到开发与 探索的平衡。粒子的新位置和速度将用公式(21 (18) 名a(e+f-x-e(到-1- 和(22)更新。 =+c;rand(pbest)+ ezrand(gbest).i=1.2.N (21) =对 *, 根据对偶原理将原问题转化为公式(19) 其中,℃,和2是加速度系数,分别调整最大步 径,以达到全局最佳拉子和单个最佳拉子:阳nd是随 机数均匀分布在「0.1上)是惯性重量,保持全局和局 部搜索能力的平衡:N表示粒子数:k表示当前迭代 s(a+d)+∑a-c)川 的次数:,指定粒子速度;x,指定位置:pbes,是粒了 约束条件: 局部最佳位置:gbs1,是所有粒子的全局最佳位置。 使用表2中的参数构建PS0优化算法,将惩罚 (m-a)=0.0≤a≤c.0≤a≤c(1 系数C和核函数参数y作为PS0的两类鸟群,每次 其中,K(x,)=(x)T(x),本文中使用的 迭代后重新更新鸟群位置,直到达到迭代次数时停 K·,为RBF核函数。 止。使用PS0优化SVR的步骤见表3 SVR的最终预测模型为公式(20 PS0算法参数说明 criptio )=∑(a,-a)x,)+b(20) 参数 取值 SVR中惩罚系数C和RBF核函数的参数y会 轻子。 C.y 对最终的拟合效果产生较大的影响,其原因为:惩罚 授索空间维数d 系数C用来全衡损失和分类间隔的权重,如果洗料 粒子数细 错误会造成硬间隔或是过拟合的情况:参数y影 个体学习因子 高斯函数的幅宽,进而影响数据在高维空间的映射 社会学习因子 惩罚系数C和核函数参数y的选取非常重要,但是 惯性因子 对于如何选取这两个参数却没有明确的理论依据。 0。 3.2.2PS0模型原理及训练 基于SVR参数选择不确定性的问题,本文提出 选代次数 100 优化SVR步 on SVR steps Stp1:初始化粒子群算法的粒子群.生成初始位置x和速度■,设置粒子群算法的初始参数: srp2:将样本序列集和样本测试集分开,寻找各自的极值bs,和全局极值grs: step3:按照公式(2)和公式(2进行选代更新以及 在此基础上,得到了全局极值此可用作SVR的最优参数:忽罚系数C和核函数参数 s:利用上一步得到的最优参数和训练样本集训练SVR模型: Sp:使用测试样本集米评估上述训练的sSVR的预测性能。 C)19942022Chim ademic Journal Elec tronie Publishing House.All rights reserved. http://www.cnki.ne
引入拉格朗日乘子 αi,αi * ,ηi 和 ηi * ,相应的拉 格朗日方程为公式( 18) : L( ω,ξ,ξ * ) = 1 2 ‖ω‖2 + C∑ n i = 1 ( ξ + ξ * ) - ∑ n i = 1 αi ε + ξ - yi ( ) + ωφ( x) + b - ∑ n i = 1 αi * ( ε + ξ - yi - ωφ( x) - b) - ∑ n i = 1 ( λξ + λ* ξ * ) ( 18) 根据对偶原理将原问题转化为公式( 19) : max α,α* { - 1 2 ∑ l i = 1 ∑ l j = 1 ( αi - α* i ) ( αj - α* j ) * K( xi,xj ) - ε∑ l i = 1 ( αi + α* i ) + ∑ l i = 1 yi ( αi - α* i ) } 约束条件: ∑ l i = 1 ( αi - αi * ) = 0,0 ≤ αi ≤ C,0 ≤ α* i ≤ C ( 19) 其中,K( xi,xj ) = φ( xi ) T φ( xj ) ,本文中使用的 K(·,·) 为 RBF 核函数。 SVR 的最终预测模型为公式( 20) : f( x) = ∑ l i = 1 ( αi - α* i ) K( xi,xj ) + b ( 20) SVR 中惩罚系数 C 和 RBF 核函数的参数 γ 会 对最终的拟合效果产生较大的影响,其原因为: 惩罚 系数 C 用来全衡损失和分类间隔的权重,如果选择 错误会造成硬间隔或是过拟合的情况; 参数 γ 影响 高斯函数的幅宽,进而影响数据在高维空间的映射。 惩罚系数 C 和核函数参数 γ 的选取非常重要,但是 对于如何选取这两个参数却没有明确的理论依据。 3.2.2 PSO 模型原理及训练 基于 SVR 参数选择不确定性的问题,本文提出 使用 PSO 算法选取参数来改进 SVR 模型。PSO 是 一种基于种群的随机搜索算法,用于解决无约束优 化问题[9]。在粒子生成过程中,粒子根据自身的经 验以及相邻粒子的经验改变其位置。PSO 系统将局 部搜索方法与全局搜索策略相结合,以达到开发与 探索的平衡。粒子的新位置和速度将用公式( 21) 和( 22) 更新。 v k+1 i = ωv k i + c1 rand( pbest k i - xk i ) + c2 rand( gbest k i - xk i ) ,i = 1,2,.,N ( 21) xk+1 i = xk i + v k+1 i ( 22) 其中,c1 和 c2 是加速度系数,分别调整最大步 径,以达到全局最佳粒子和单个最佳粒子; rand 是随 机数均匀分布在[0,1]; ω 是惯性重量,保持全局和局 部搜索能力的平衡; N 表示粒子数; k 表示当前迭代 的次数; vi 指定粒子速度; xi 指定位置; pbes ti 是粒子 局部最佳位置; gbes ti 是所有粒子的全局最佳位置。 使用表 2 中的参数构建 PSO 优化算法,将惩罚 系数 C 和核函数参数 γ 作为 PSO 的两类鸟群,每次 迭代后重新更新鸟群位置,直到达到迭代次数时停 止。使用 PSO 优化 SVR 的步骤见表 3。 表 2 PSO 算法参数说明 Tab. 2 PSO algorithm parameter description 参数 取值 粒子 x C,γ 搜索空间维数 d 2 粒子数量 N 50 个体学习因子 c1 2 社会学习因子 c2 2 惯性因子 ω 0.5 r1 0.8 r2 0.3 迭代次数 100 表 3 PSO 优化 SVR 步骤 Tab. 3 PSO optimization SVR steps 步骤 Step1: 初始化粒子群算法的粒子群,生成初始位置 xi 和速度 vi,设置粒子群算法的初始参数; Step2: 将样本序列集和样本测试集分开,寻找各自的极值 pbesti 和全局极值 gbesti ; Step3: 按照公式( 21) 和公式( 22) 进行迭代更新以 vi 及 xi ; Step4: 根据种群适应度值更新 pbesti 和 gbesti ; Step5: 返回全局最优参数。该数据集所需的最优核函数是根据最优核参数对应的核函数来确定的, 在此基础上,得到了全局极值 gbesti 可用作 SVR 的最优参数: 惩罚系数 C 和核函数参数 γ; Step6: 利用上一步得到的最优参数和训练样本集训练 SVR 模型; Step7: 使用测试样本集来评估上述训练的 SVR 的预测性能。 第 7 期 张文艳,等: 基于肌肉激活度的关节运动角度分层预测 105