
电子与宏观物体具有完全不同的特点, 不能同时准确地确定它的位置和动能,而只 能达到一定的近似程度。电子的位置确定得 越准确(△X越小),则电子的动量就确定得越 不准确(△,越大);反之,电子的动量确定得 越准确,电子的位置就确定得越不准确
电子与宏观物体具有完全不同的特点, 不能同时准确地确定它的位置和动能,而只 能达到一定的近似程度。电子的位置确定得 越准确( 越小),则电子的动量就确定得越 不准确( 越大);反之,电子的动量确定得 越准确,电子的位置就确定得越不准确。 x x p

第二节 氢原子结构 一、Schrodinger方程 二、波函数 三、四个量子数 四、氢原子波函数的角度分布图形 五、氢原子的径向分布图
第二节 氢原子结构 一、 方程 二、波函数 三、四个量子数 四、氢原子波函数的角度分布图形 五、氢原子的径向分布图 Schrodinger

一、Schrodinger方程 1926年,奥地利著名的物理学家Schrodinger 首先提出描述了电子运动状态的波动方程,称为 Schrodinger方程: 8w aw 0z2 8元m(E-V)W h2 方程的每一个解W,就表示电子的一种运动状态, 与山相应的E就是电子在这一运动状态下的能量。 至今只能准确求解单电子原子的Schrodinger 方程。而即使是对单电子原子,求解Schrodinger 方程也很复杂,需要较深的数学知识
一、 方程 1926年,奥地利著名的物理学家 首先提出描述了电子运动状态的波动方程,称为 方程: 2 2 2 2 2 2 2 2 8π ( ) m E V x y z h + + = − − 方程的每一个解 ,就表示电子的一种运动状态, 与 相应的E 就是电子在这一运动状态下的能量。 Schrodinger Schrodinger 至今只能准确求解单电子原子的 方程。而即使是对单电子原子,求解 方程也很复杂,需要较深的数学知识。 Schrodinger Schrodinger Schrodinger
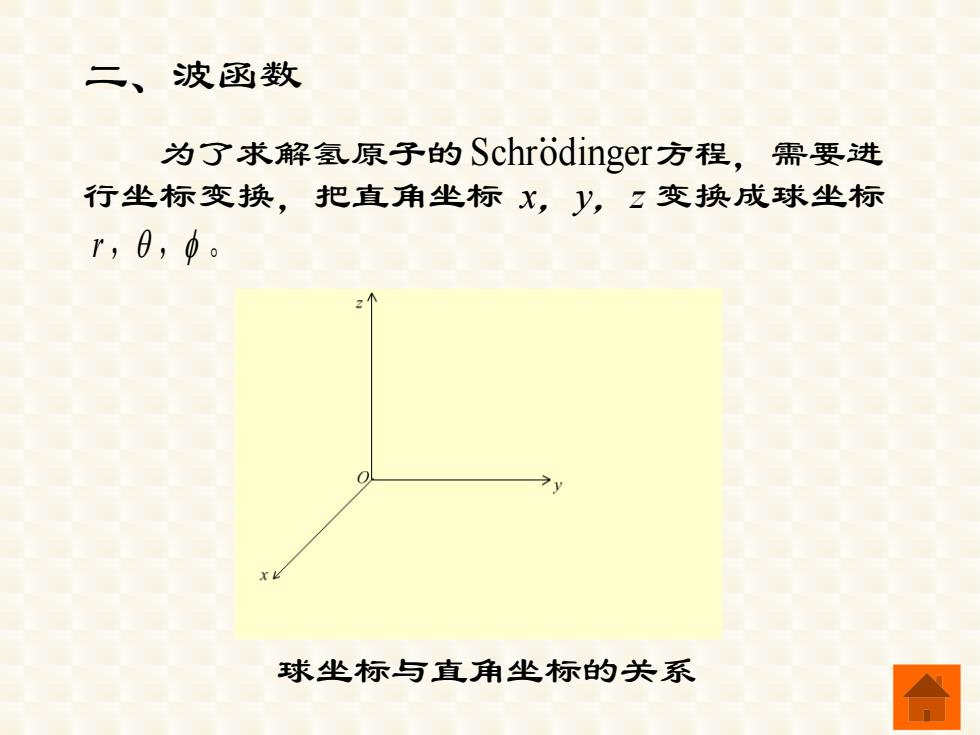
二、波函数 为了求解氢原子的Schrodinger方程,需要进 行坐标变换,把直角坐标x,y,z变换成球坐标 r,0,0。 球坐标与直角坐标的关系
二、波函数 为了求解氢原子的 方程,需要进 行坐标变换,把直角坐标 x,y,z 变换成球坐标 r , , 。 球坐标与直角坐标的关系 Schrodinger

从Schrodinger方程解出来的波函数,是球坐 标r,0,中的函数式,记为yW(r,0,中),常将波函数 分解为两个函数的乘积: w(r,0,)=R(r)Y(0,) 电子在原子核外空间的运动状态,可以用波 函数山来描述,每一个山就表示电子的一种运动 状态,通常把波函数称为原子轨道
从 方程解出来的波函数,是球坐 标 的函数式,记为 常将波函数 分解为两个函数的乘积: 电子在原子核外空间的运动状态,可以用波 函数 来描述,每一个 就表示电子的一种运动 状态,通常把波函数称为原子轨道。 ( , , ) ( ) ( , ) r R r Y = r, , ( , , ) r Schrodinger