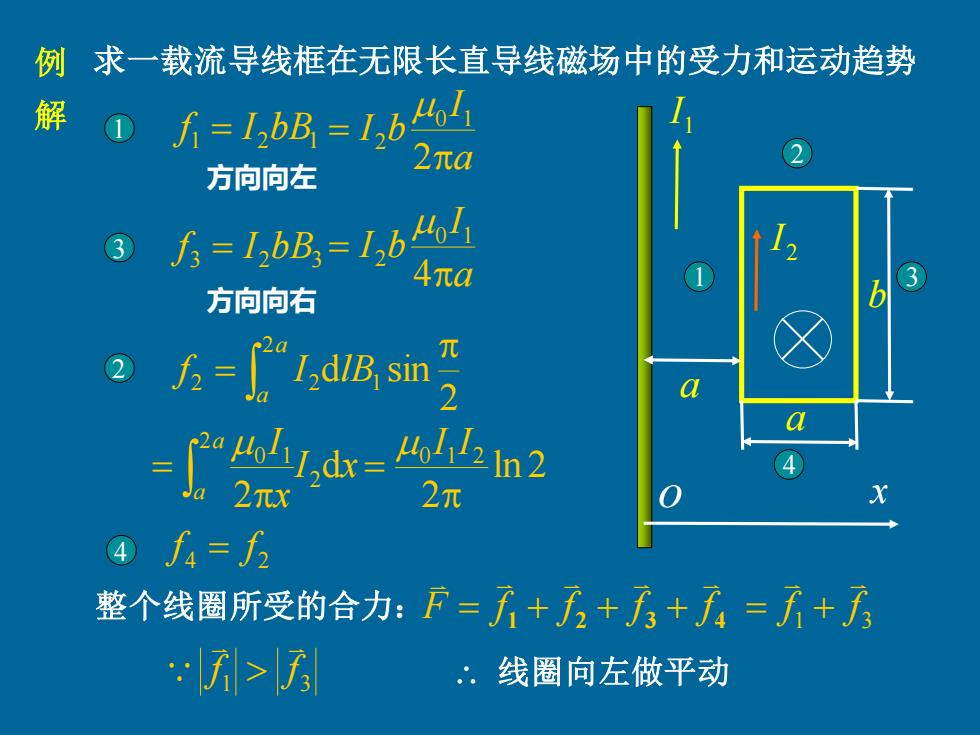
例求一载流导线框在无限长直导线磁场中的受力和运动趋势 ①才=1,bB=1,b 解 2πa 方向向左 3 方=1bB=1,b4 4元0 方向向右 a方=1,dBsn a a =“n2 2元X 2元 ④f=f2 整个线圈所受的合力:F=无+方+方+万:=才+方 f引>万 .线圈向左做平动
例 求一载流导线框在无限长直导线磁场中的受力和运动趋势 解 1 I a b a 2 I 1 2 3 4 o x 1 2 1 f = I bB a I I b = 2 0 1 2 3 2bB3 f = I a I I b = 4 0 1 2 方向向左 方向向右 = a a f I lB 2 2 2 1 2 d sin I x x a I a d 2 2 2 0 1 = ln 2 2 0 1 2 = I I 4 2 f = f 整个线圈所受的合力: 1 2 3 4 F f f f f = + + + 1 3 f f = + f 1 f 3 线圈向左做平动 1 3 2 4
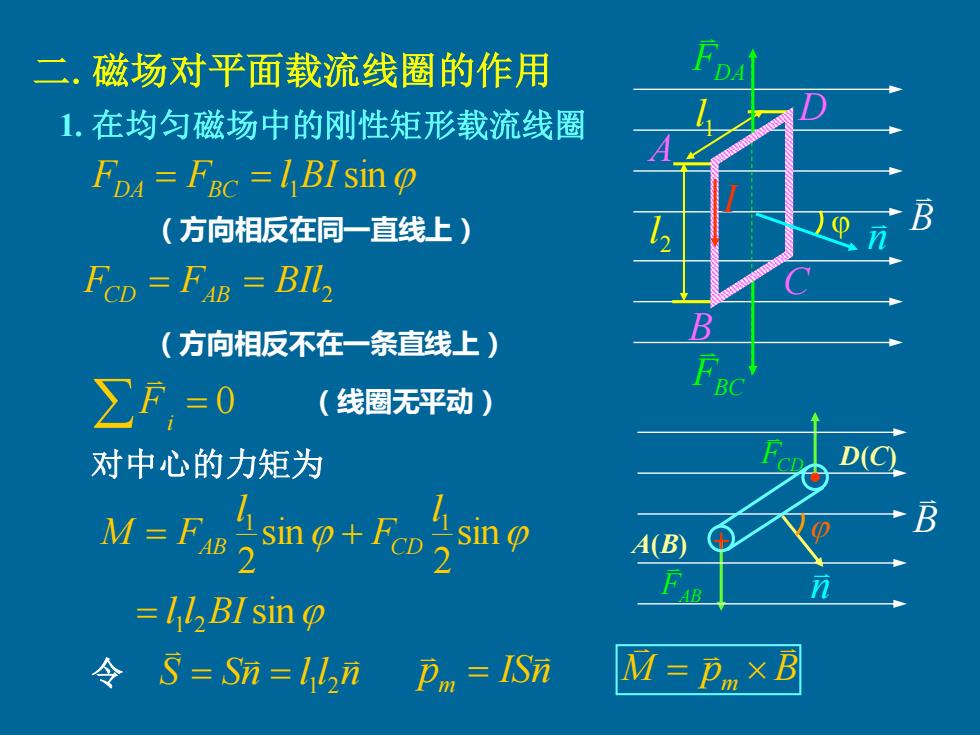
二.磁场对平面载流线圈的作用 D 1.在均匀磁场中的刚性矩形载流线圈 FDA=FRc=BIsin (方向相反在同一直线上) FCD=FAB BIL (方向相反不在一条直线上) ∑F,=0 (线圈无平动) 对中心的力矩为 M=F分 sin A(B) =Il,BI sin o 令 S Sn=lln D ISn M=Pn×B
FCD FAB 二.磁场对平面载流线圈的作用 B 1 l 2 l FDA FBC D C B A I FDA = FBC = l 1BIsin (方向相反在同一直线上) FCD = FAB = BIl2 = 0 i F (线圈无平动) 对中心的力矩为 sin 2 sin 2 1 1 l F l M = FAB + CD = l 1 l 2BIsin 1. 在均匀磁场中的刚性矩形载流线圈 n (方向相反不在一条直线上) S Sn l l n = = 1 2 M pm B p ISn = m 令 = B + n A(B) D(C)

2.磁场力的功 dA=-Mdp=-BISsin odo负号表示力矩作正功时p减小 =ld(BS cosp)=IdΦm 4= 1dpn=I(ΦDm2-Dni)=△① m 讨论 (1)线圈若有N匝线圈 M=pm×B (2)M作用下,磁通量增加 0=0M=0 稳定平衡 0三π M=0 非稳定平衡 (3)非均匀磁场中的平面电流环 ∑F,≠0 M≠0 线圈有平动和转动
2. 磁场力的功 dA = −Md = −BIS sind m = Id(BS cos) = Id m m m m A I I I m m = = − = d ( ) 2 1 2 1 讨论 (1) 线圈若有N 匝线圈 M Npm B = (2) M 作用下,磁通量增加 M = 0 = 0 稳定平衡 负号表示力矩作正功时 减小 = M = 0 非稳定平衡 (3) 非均匀磁场中的平面电流环 0 i F M 0 线圈有平动和转动

s9.6 带电粒子在磁场中的运动 一.洛伦兹力公式 ·实验结果 f ocg,B,v,sin B =quBsin0 fn=qDx×B ·安培力与洛伦兹力的关系 F=IdT x B =nsqudI x B dF =NgD×B→ dN 7=9D×B=7 安培力是大量带电粒子洛伦兹力的叠加
一.洛伦兹力公式 • 实验结果 q B v f f q,B,v,sin θ f = qvBsin • 安培力与洛伦兹力的关系 l d I q s q B f N F = v = d d fm q B = v F I l B = d nsq l B = vd Nq B = v 安培力是大量带电粒子洛伦兹力的叠加 §9.6 带电粒子在磁场中的运动 v

讨论 ()洛伦兹力始终与电荷运动方向垂直,故千对电荷不作功 (2)在一般情况下,空间中电场和磁场同时存在 F=。+m=gE+qD×B=dp/d 二,带电粒子在均匀磁场中的运动 )⊥B情祝 quBsin=m R ● R gB ·粒子回转周期与频率 2元R 2πm gB 2m
(1) 洛伦兹力始终与电荷运动方向垂直,故 讨论 f 对电荷不作功 (2) 在一般情况下,空间中电场和磁场同时存在 F f e fm = + qE q B = + v dp / dt = 二.带电粒子在均匀磁场中的运动 • B v ⊥ B f q R q B m 2 2 sin v v = qB m R v = qB R m T = = 2 2 v m qB f = 2 • 粒子回转周期与频率 情况 v