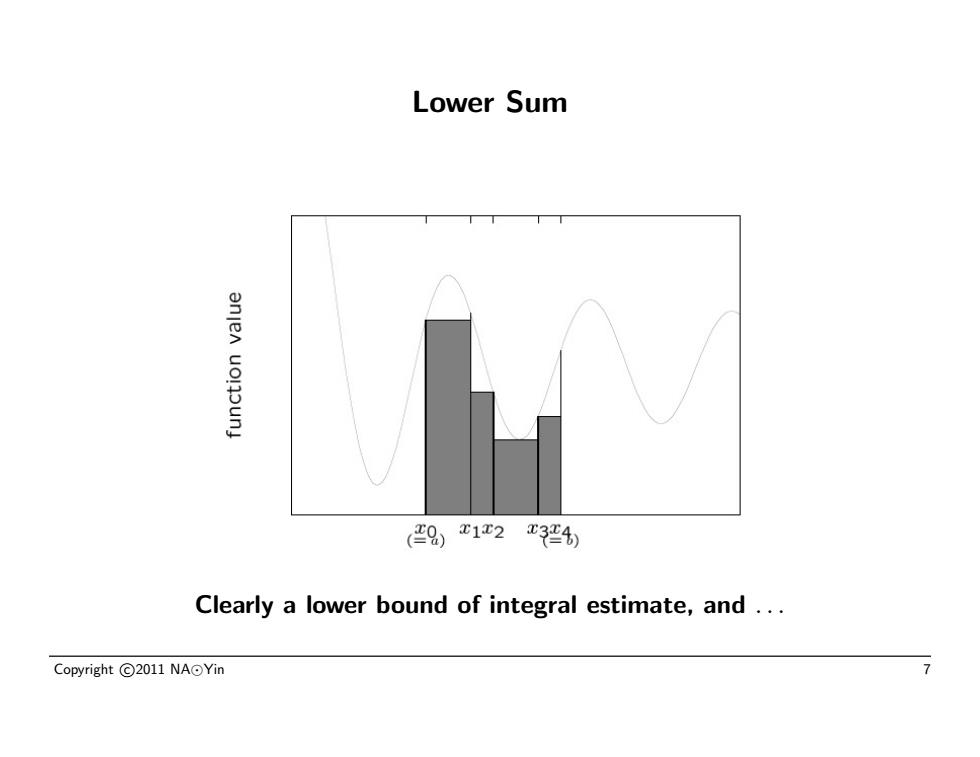
Lower Sum anjen uollunj 9)x1x2r4) Clearly a lower bound of integral estimate,and... Copyright©2011NA⊙Yin 7
Lower Sum Clearly a lower bound of integral estimate, and . . . Copyright c 2011 NA Yin 7
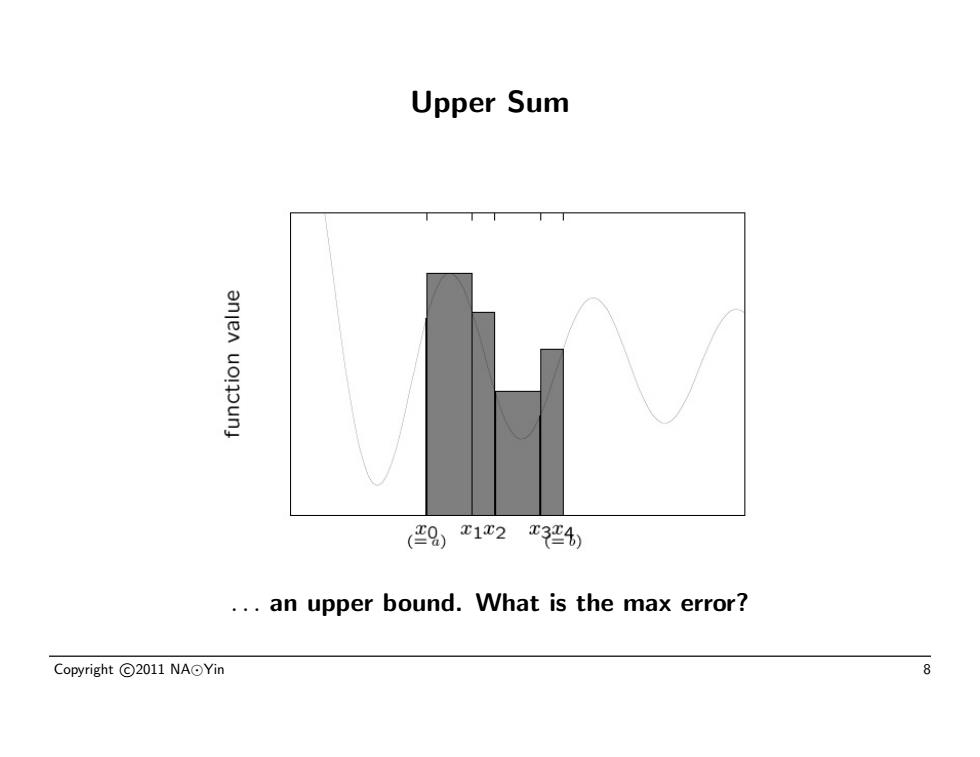
Upper Sum anjen uoloun 9x12r4 ..an upper bound.What is the max error? Copyright©2011NA⊙Yin 8
Upper Sum . . . an upper bound. What is the max error? Copyright c 2011 NA Yin 8

Example Third method.use lower and upper sums:(L+U)/2 ●f(x)=x2,[a,b=[0,1andP={0,,2,,1} ·L=品,U=2 ·(L+U)/2=是(actual) .naive approach:still error of ●Max error:(U-L)/2= Is this good enough? Copyright©2011NA⊙Yin
Example • Third method. use lower and upper sums: (L + U)/2 • f(x) = x 2 , [a, b] = [0, 1] and P = {0, 1 4 , 1 2 , 3 4 , 1} • L = 7 32, U = 15 32 • (L + U)/2 = 11 32 (actual 1 3 ) • naive approach: still error of 1 96. • Max error: (U − L)/2 = 1 8 Is this good enough? Copyright c 2011 NA Yin 9

Rethinking Perhaps lower and upper sums are enough? error seems small work seems small as well But:estimate of max error was not small ( ·Do they converge to integral as n→o? Will the extrema always be easy to calculate?Accurately?(Probably not!) Proceed in theoretical and practical directions. Copyright©2011NA⊙Yin 10
Rethinking • Perhaps lower and upper sums are enough? ∗ error seems small ∗ work seems small as well • But: estimate of max error was not small (1 8 ) • Do they converge to integral as n → ∞? • Will the extrema always be easy to calculate? Accurately? (Probably not!) Proceed in theoretical and practical directions. Copyright c 2011 NA Yin 10

Numerical Quadrature ·Introduction →Riemann Integration Composite Trapezoid Rule Composite Simpson's Rule ●Gaussian Quadrature Copyright©2011NA⊙Yin 11
Numerical Quadrature • Introduction ⇒ Riemann Integration • Composite Trapezoid Rule • Composite Simpson’s Rule • Gaussian Quadrature Copyright c 2011 NA Yin 11