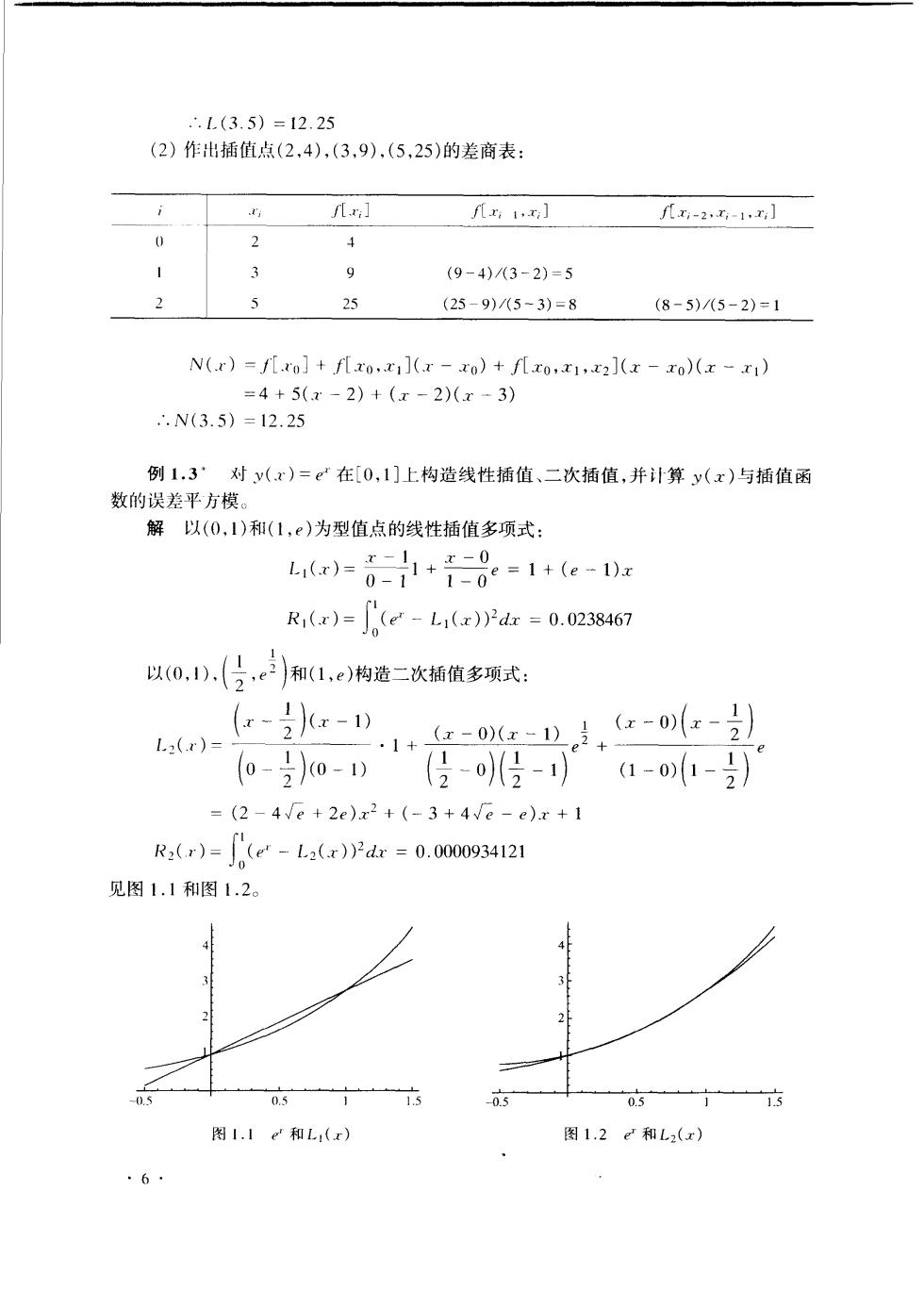
L(3.5)=12.25 (2)作出插值点(2,4),(3,9),(5,25)的差商表: r, x1] x-2x-1x】 0 2 4 3 9 (9-4)/八3-2)=5 5 25 (25-9)/(5-3)=8 (8-5)/(5-2)=1 N(r)=]+fro.ri](r-xo)+flro.x1.2](x ro)(x-z1) =4+5(x-2)+(x-2)(x-3) ∴.N(3.5)=12.25 例1.3°对v(x)=e在[0,1]上构造线性插值、二次插值,并计算y(x)与插值函 数的误差平方模。 解以(0,1)和(1,e)为型值点的线性插值多项式: h)0-+8=1+e-0x R1(x)=(e-L1(x)2dx=0.0238467 以(0.1).(兮)和(1,e)构造二次插值多项式 L2(.x)= ·1+ -业,-o- o-o-n(日-3-)a-4-】 =(2-4e+2e)x2+(-3+4e-e).x+1 R2(r)=(e-L2(.x)2dx=0.0000934121 见图1.1和图1.2。 图1.1e和L(x) 图1.2e和L2(x) 6

请读者完成以下练习: (1)分别计算L1(.x)和L2(x)的误差界: (2)分别计算在[0,0.5],[0.5,1]区间e与L1(x),L2(x)的误差平方模。 例1.4设f(.x)=x2-2.x+1.2,x,和f(,)取值如下: -1 -0.5 0 0.3 f,) 4.2 2.45 1.2 0.45 0.2 分别构造L2(.x),L(x),L(.x),并比较结果。 解以(-1.4.2),(0,1.2)和(1,0.2)为插值点,则 w8×42+06=书x12 =x2-2+1.2 以(-1,4.2),(-0.5,2.45),(0,1.2)和(1,0.2)为插值点,则 L3(.)=r-2x+1.2 以(-1,4.2),(-0.5,2.45),(0,1.2).(0.5.0.45)和(1,0.2)为插值点,则 L4(x)=x2-2x+1.2 ·f3(x)=0, .R(r)=0,n≥2,有f(x)=Ln(x),n≥2。 请体会(1.1)式n次拉格朗日插值多项式的定义“给定(x,f(x)(i=0,1,.,n: 互不相同),构造次数至多为!的插值多项式L(x)”中“至多”两个字的含意。 例1.5设f(x)∈C2[a,b],由(a,f(a)和(b,f(b)构造的插值函数为L1(.x) 则有 IR()l =If(r)-L(x)8(b-a)2M2 其中M2=max广(x)川。 证 Ri(r)=Rx)-L()=((r-a)(-) 2 g(r)=(x-a)(.x-b) g0)=x-6+-a=2:-(6+a.g(0)=0 r=“十是1g(x)1的极大值点 7

1R(x1=上1z-aj(z-b 2 ≤警1-je-川 -k(b-a)M: 1R,(e1≤0(6-eP 例1.6设f(x)∈C2[a,b],且f(a)=f(b)=0,证明: l1fx1≤g(b-aPM2.a≤x≤b 其中M,=af(x)1。 证做(a,f(a),(b,f(b)的线性插值函数,显然有L1(x)=0。又 f(x)=L(x)+R1(x) -8a)+言号o)+是:- =(E)(x-a)(x-6) 2 由例1.5有 1fx1≤日(b-aPM, 例1.7给出函数表: x 1.05 1.10 1.15 1.20 f() 2.13 2.20 2.17 2.32 构造分段线性插值函数,计算f(1.065)的近似值。 解 p(x)=)=二)+ xi-xi+l 1.065∈[1.05,1.10] 6)=610×213+70106x220 -1.05 f(1.065)≈p(1.065)=g(1.065)=2.151 例1.8已知等距插值点x0,x1,x2,证明:二次插值多项式的误差界为 1R,1号,r 8

其中h=x2-x1=x1-x0。 证设L2(x)是由插值点(x:,f(x,)(i=0,1,2)构造的插值多项式,由插值误差的 定义: R:()=f)-Lxz)-A((-0) 31 令x=x0+h,0≤t≤2,则x=x0+h,i=0,1,2。 1R:(1≤,f(xi1x-zox-xz-xl h3 =3股,f(x)l(-1-2川 <,a,0.-2训 (*) 计算g(t)=t(t-1)(t-2)在t∈[0,2]的极大值: g)=3-6+2,e1后g=1+有 &o=0.ge)-25&g=-2g5.e2)=0 在 袋,go1.29 代人(*)式,得 R(xl≤2号竖f() 例1.9设fx,x0,x1,x]是x的m次多项式,证明:f[x,x0,x4,x4+1]是 x的m-1次多项式。 证 F(x)=fx,0,4,l=z,o]-0,l I -ZH+I (x-x4+i)f[x,x0,.,x,+1]=f[x,x0,.,]-fx0,x1,.,xk,x+i] 当x二x+1时,f儿x,x0,.,]一f八x0,.,x4+1]=0。即等式右端分子有x x+因式,故F(x)=f几x,x0,x,x+1]为x的m-1次多项式。 请读者思考:若f(x)是n次多项式,则f[x,x0,.,xn]是几次多项式?它的值等于 多少? 例1.10设f(x)=x3-3x3+x-1,计算差商: f[30,3],f3,3,.,35],f3,3,.,3] 9

39,3y=3】-83 3-1 (x)=5I fK6)(.x)=0 f39.3,.,3-9=1 51 30,3.,3的]==0 6! 例1.11设f(x)eC[a,b],xo∈(a,b),定义x0,x]=imx,zo]。证明: fxo,xo]=f(xo) 证由微分中值定理,有 x,n1=)二=fo+6(x-o》.0<9<1 r-xo .nro.ro]lim f]im(o+(-))=f (ro) 点评:该结论应用在差商计算中,解决了含有给定函数值和导数值组合的差商计算, 即用牛顿插值方法构造埃尔米特插值多项式。 例1.12给定f(xo),f(x1),f(x0),构造满足上述插值条件的二次插值多项式 H(x) 解方法1,设H(x)=co+c1(x-x0)+c2(x-xo)2。 由H(xo)=f(x0),得 co=f(xo) 由(xo)=f(xo),得 c1=f(xo) 由H(x1)=f(x1),H(x1)=f(xo)+(x1-xo)f(xo)c2(x1-xo)2=fx1),得 a-f)-fo)-(✉-orxo (x1-x0)2 H)=fo)+(x-0ro)+)-fw)-(co)f (ro-oP (x1-xo2 方法2,构造差商型埃尔米特插值函数H(x): 之, f() f几为-1名] f几4-2-1] 0 20=x0 f(zo) z1=.x0 f(1) f(ro) 2 2=x1 f2) fx0,x1】 fxo.]-f(xo) x1-r0 ·10·