
Maxwell关系 dG=-Sdr+Vdp+∑dN 化学势随温度的改变 84y ap ) 化学势随压强的改变 畿 组元会影响其他组元
Maxwell 关系 𝑑𝐺 = −𝑆𝑑𝑇 + 𝑉 𝑑𝑝 + ∑ 𝑖 𝜇𝑖𝑑𝑁𝑖 ( 𝜕𝑆 𝜕 𝑝 ) 𝑇 {𝑁𝑖 } = − ( 𝜕𝑉 𝜕𝑇 ) 𝑝{𝑁𝑖 } ( 𝜕𝑆 𝜕𝑁𝑖 ) 𝑇 𝑝{𝑁𝑗≠𝑖 } = − ( 𝜕𝜇𝑖 𝜕𝑇 ) 𝑝{𝑁𝑗 } ✞ ✝ ☎ 化学势随温度的改变 ✆ ( 𝜕𝑉 𝜕𝑁𝑖 ) 𝑇 𝑝{𝑁𝑗≠𝑖 } = ( 𝜕𝜇𝑖 𝜕 𝑝 ) 𝑇 {𝑁𝑗 } ✞ ✝ ☎ 化学势随压强的改变 ✆ ( 𝜕𝜇𝑖 𝜕𝑁𝑗 ) 𝑇 𝑝{𝑁𝑘≠𝑗 } = ( 𝜕𝜇𝑗 𝜕𝑁𝑖 ) 𝑇 𝑝{𝑁𝑘≠𝑖 } ✞ ✝ ☎ 组元会影响其他组元 ✆

Gibbs-.Duhem关系 单组元 G(T,p,N)=Ng(T,p)=Nu(T,p) N=N1+++M=∑N u=Ts-pv+8=Ts-ps+u xi Ni/N ∑= k-1个强度量+一个广延量N U=Nu S=Ns V=Nv... U=U(Ns,Nv,{Nxi})=Nu(s,v,{xi}) dU Ndu udN =Tds-paW+∑dw =NTds-Npd+N∑aidi+(Ts-pv+∑xi)dN W=u(s,》=Ts-pv+∑: Gibbs-Duhem关系 du Tds-pdv ∑4d, 仍把x看成k个独立变量 霉考虑强度量时,总摩尔数N起的作用并不大一冗余参数
Gibbs-Duhem 关系 𝑁 = 𝑁1 + 𝑁2 + · · · + 𝑁𝑘 = ∑ 𝑖 𝑁𝑖 𝑥𝑖 = 𝑁𝑖/𝑁 ∑ 𝑖 𝑥𝑖 = 1 ☞ ✞ ✝ ☎ ✆ 𝑘 − 1 个强度量 + 一个广延量 𝑁 𝑈 = 𝑁𝑢 𝑆 = 𝑁 𝑠 𝑉 = 𝑁𝑣 · · · 𝑈 = 𝑈(𝑁 𝑠, 𝑁𝑣, {𝑁𝑥𝑖}) = 𝑁𝑢(𝑠, 𝑣, {𝑥𝑖}) 𝑑𝑈 = 𝑁 𝑑𝑢 + 𝑢𝑑𝑁 = 𝑇 𝑑𝑆 − 𝑝𝑑𝑉 + ∑ 𝑖 𝜇𝑖𝑑𝑁𝑖 = 𝑁𝑇 𝑑𝑠 − 𝑁 𝑝𝑑𝑣 + 𝑁 ∑ 𝑖 𝜇𝑖𝑑𝑥𝑖 + (𝑇 𝑠 − 𝑝𝑣 + ∑ 𝑖 𝑥𝑖𝜇𝑖)𝑑𝑁 𝑢 = 𝑢(𝑠, 𝑣, {𝑥𝑖}) = 𝑇 𝑠 − 𝑝𝑣 + ∑ 𝑖 𝑥𝑖𝜇𝑖 ☞ ✞ ✝ ☎ ✆ Gibbs-Duhem 关系 𝑑𝑢 = 𝑇 𝑑𝑠 − 𝑝𝑑𝑣 + ∑ 𝑖 𝜇𝑖𝑑𝑥𝑖 ☞ ✞ ✝ ☎ 仍把 ✆ 𝑥𝑖 看成 𝑘 个独立变量 ☞考虑强度量时,总摩尔数 𝑁 起的作用并不大 ⇒ 冗余参数。 ✗ ✖ ✔ ✕ 单组元 𝐺(𝑇, 𝑝, 𝑁) = 𝑁𝑔(𝑇, 𝑝) = 𝑁 𝜇(𝑇, 𝑝) 𝑢 = 𝑇 𝑠 − 𝑝𝑣 + 𝑔 = 𝑇 𝑠 − 𝑝𝑠 + 𝜇

Gibbs-Duhem关系 M=Ts-pv+∑x4 d=Tds-pdw+∑hd U=TS-pV+∑NMw G=G(T,p.{)=U-TS+pV=∑N4=N∑x,T,p,) 8=8(T,p,xi)=G/N=∑x s=r+咖+∑4 ∑:x=1,只有k-1个独立的x Maxwell关系
Gibbs-Duhem 关系 𝑢 = 𝑇 𝑠 − 𝑝𝑣 + ∑ 𝑖 𝑥𝑖𝜇𝑖 𝑑𝑢 = 𝑇 𝑑𝑠 − 𝑝𝑑𝑣 + ∑ 𝑖 𝜇𝑖𝑑𝑥𝑖 𝑈 = 𝑇 𝑆 − 𝑝𝑉 + ∑ 𝑖 𝑁𝑖𝜇𝑖 𝐺 = 𝐺(𝑇, 𝑝, {𝑁𝑖}) = 𝑈 − 𝑇 𝑆 + 𝑝𝑉 = ∑ 𝑖 𝑁𝑖𝜇𝑖 = 𝑁 ∑ 𝑖 𝑥𝑖𝜇𝑖(𝑇, 𝑝, {𝑥𝑖}) 𝑔 = 𝑔(𝑇, 𝑝, {𝑥𝑖}) = 𝐺/𝑁 = ∑ 𝑖 𝑥𝑖𝜇𝑖 𝑑𝑔 = −𝑠𝑑𝑇 + 𝑣𝑑𝑝 + ∑ 𝑘 𝑖=1 𝜇𝑖𝑑𝑥𝑖 ✞ ✝ ☎ ✆ ∑ 𝑖 𝑥𝑖 = 1,只有 𝑘 − 1 个独立的 𝑥𝑖 Maxwell 关系 ( 𝜕𝑠 𝜕 𝑝 ) {𝑥𝑖 } = − ( 𝜕𝑣 𝜕𝑇 ) {𝑥𝑖 } ( 𝜕𝜇𝑖 𝜕𝑥 𝑗 ) 𝑇 𝑝{𝑥𝑘≠𝑗 } = ( 𝜕𝜇𝑗 𝜕𝑥𝑖 ) 𝑇 𝑝{𝑥𝑘≠𝑖 } · · ·

巨势 J=JT,V,》=F-∑N dF=-SdT-pdW+∑hdN, dW=-sdr-pdW-∑N,d, J=F->Niui=F-G=F-(F+pV)=-pV =-p(T,V,{4})V 这里的压强是以温度、体积和化学势为自变量,和普通状态 方程不同。例如从理想气体的状态方程J=-pV=-NRT= -N(T,V,)RT并不包含所有热力学性质。 露巨势主要用于处理和粒子源接触的系统 统计物理中巨势可以用巨正则系综计算
巨势 𝐽 = 𝐽 (𝑇, 𝑉, {𝜇𝑖}) = 𝐹 − ∑ 𝑖 𝑁𝑖𝜇𝑖 𝑑𝐹 = −𝑆𝑑𝑇 − 𝑝𝑑𝑉 + ∑ 𝑖 𝜇𝑖𝑑𝑁𝑖 𝑑𝐽 = −𝑆𝑑𝑇 − 𝑝𝑑𝑉 − ∑ 𝑖 𝑁𝑖𝑑𝜇𝑖 𝐽 = 𝐹 − ∑ 𝑖 𝑁𝑖𝜇𝑖 = 𝐹 − 𝐺 = 𝐹 − (𝐹 + 𝑝𝑉) = −𝑝𝑉 = −𝑝(𝑇, 𝑉, {𝜇𝑖})𝑉 ☞ 这里的压强是以温度、体积和化学势为自变量,和普通状态 方程不同。例如从理想气体的状态方程 𝐽 = −𝑝𝑉 = −𝑁 𝑅𝑇 = −𝑁(𝑇, 𝑉, 𝜇)𝑅𝑇 并不包含所有热力学性质。 ☞ 巨势主要用于处理和粒子源接触的系统 ☞ 统计物理中巨势可以用巨正则系综计算
5.2 混合理想气体 k个组元,N1,=Nx1,N2=Nx2,·,Nk=Nxk,N=∑iNi,x= Ni/N pVi=NiRT 分体积定律 P(∑)=pV=(∑NM)Rr=NRI PiV NiRT 分压定律 p-2m=∑-∑:
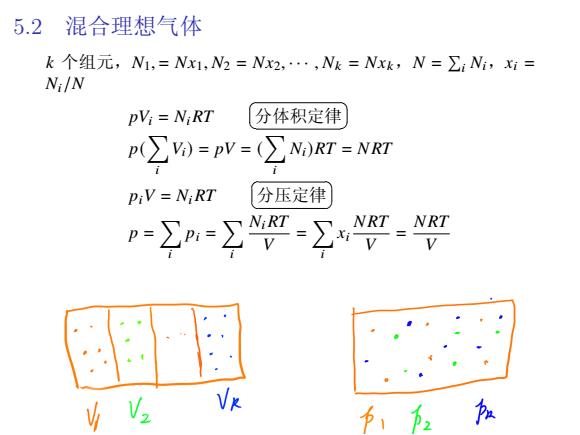
5.2 混合理想气体 𝑘 个组元,𝑁1, = 𝑁𝑥1, 𝑁2 = 𝑁𝑥2, · · · , 𝑁𝑘 = 𝑁𝑥𝑘,𝑁 = ∑ 𝑖 𝑁𝑖,𝑥𝑖 = 𝑁𝑖/𝑁 𝑝𝑉𝑖 = 𝑁𝑖𝑅𝑇 ✞ ✝ ☎ 分体积定律 ✆ 𝑝( ∑ 𝑖 𝑉𝑖) = 𝑝𝑉 = ( ∑ 𝑖 𝑁𝑖)𝑅𝑇 = 𝑁 𝑅𝑇 𝑝𝑖𝑉 = 𝑁𝑖𝑅𝑇 ✞ ✝ ☎ 分压定律 ✆ 𝑝 = ∑ 𝑖 𝑝𝑖 = ∑ 𝑖 𝑁𝑖𝑅𝑇 𝑉 = ∑ 𝑖 𝑥𝑖 𝑁 𝑅𝑇 𝑉 = 𝑁 𝑅𝑇 𝑉