西安交通大学：《材料力学 Mechanics of Materials》课程教学资源（课件讲稿）第一部分 基本变形（共六章，主讲：殷民）

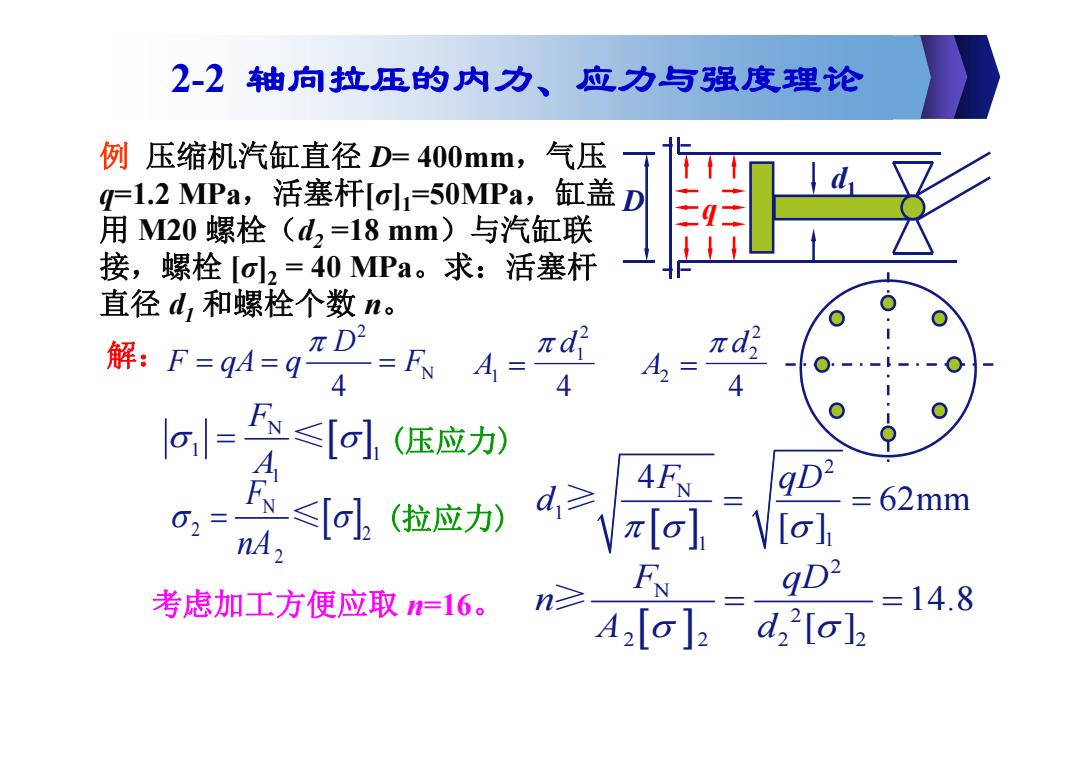
2-2轴向拉压的内力、应力与强度理论 例压缩机汽缸直径D=400mm,气压 =1.2MPa,活塞杆a1=50MPa,缸盖 用M20螺栓（d2=18mm)与汽缸联 接，螺栓o2=40MPa。求：活塞杆 直径d,和螺栓个数n。 解：F=9=9-人4- πd A2= πd 4 a=子≤[可l低应 A 9D3 62mm 0= ≤[o](拉应力) d. n☑ F 9D2 考虑加工方便应取=16。 =14.8 A2[o]2d22[o]2

例 压缩机汽缸直径 D= 400mm，气压 q=1.2 MPa，活塞杆 [ σ ] 1=50MPa，缸盖 用 M20 螺栓（ d2 =18 mm）与汽缸联 接，螺栓 [ σ ] 2 = 40 MPa。求：活塞杆 直径 d1 和螺栓个数 n 。 D q d1 解： 2 N 4 D F qA q F     A d 1 1 2 4   A d 2 2 2 4     2 N 2 22 2 2 14.8 [ ] F qD n A d   考虑加工方便应取 n=16 。 ≥     2 N 1 1 1 4 62mm [ ] F qD d   ≥     N 1 1 1 F A   ≤  (压应力)   N 2 2 2 F nA   ≤  (拉应力) 2-2 轴向拉压的内力、应力与强度理论

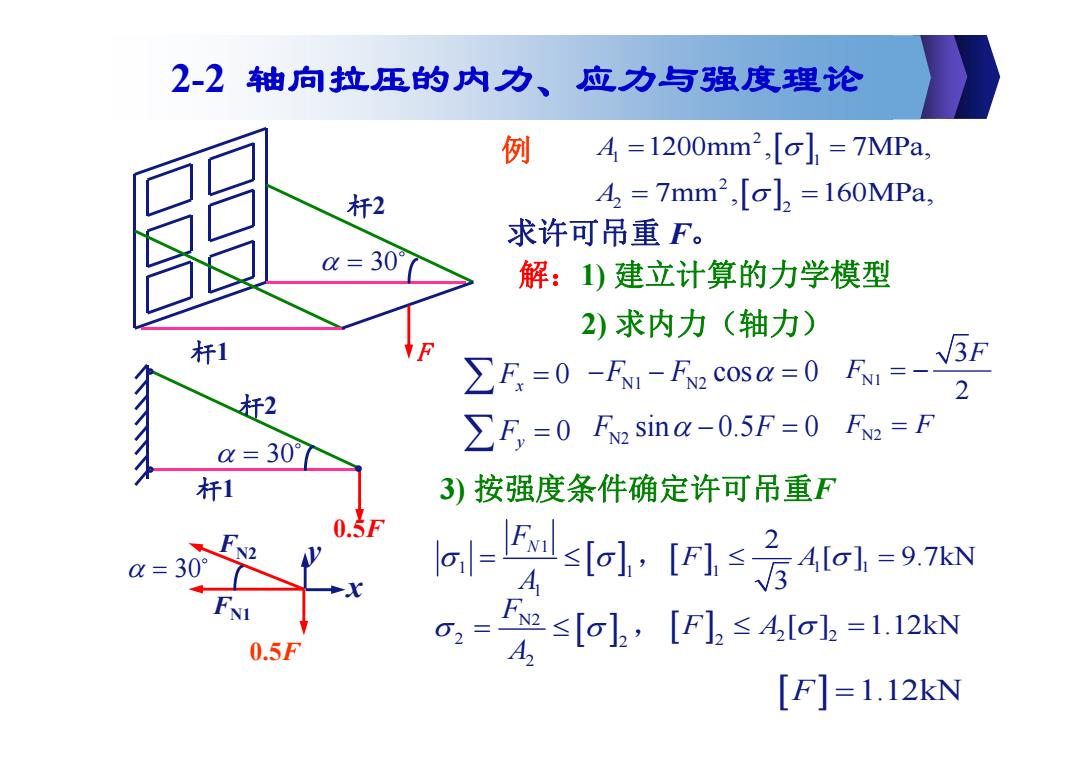
2-2轴向拉压的内力、应力与强度理论 例 4=1200mm2,[o]=7MPa, 杆2 A2=7mm2,[o]2=160MPa, 求许可吊重F。 0=30 解：1)建立计算的力学模型 2)求内力（轴力） 杆1 FNI=- √3F ∑F=0-F1-F2cosQ=0 杆2 2 0=30° >F=0 FN2 sina-0.5F=0 FN2=F 杆1 3)按强度条件确定许可吊重F 0.5F =301 -54sol,ls后4ia1=97N 0.5F 02= ≤[ol.,[Flb≤4o].=1.12kN A [F]=1.12kN

N1 N2 3 2 F F F F      0 Fx  Fy  0 N1 N2 F F  cos 0  N2 F F sin 0.5 0      2 1 1 例 A   1200mm , 7MPa,    2 2 2 A   7mm , 160MPa,  求许可吊重 F 。 F   30 杆 1 杆 2 解： FN2 FN1 0.5 F   30   1 1 1 1 FN A     ， 1 1 1 2 [ ] 9.7kN 3 F A     F  1.12kN 0.5 F   30 杆 1 杆 2 1) 建立计算的力学模型 2) 求内力（轴力） x y   N2 2 2 2 F A     ，   2 2 2 F A   [ ] 1.12kN  3) 按强度条件确定许可吊重 F 2-2 轴向拉压的内力、应力与强度理论

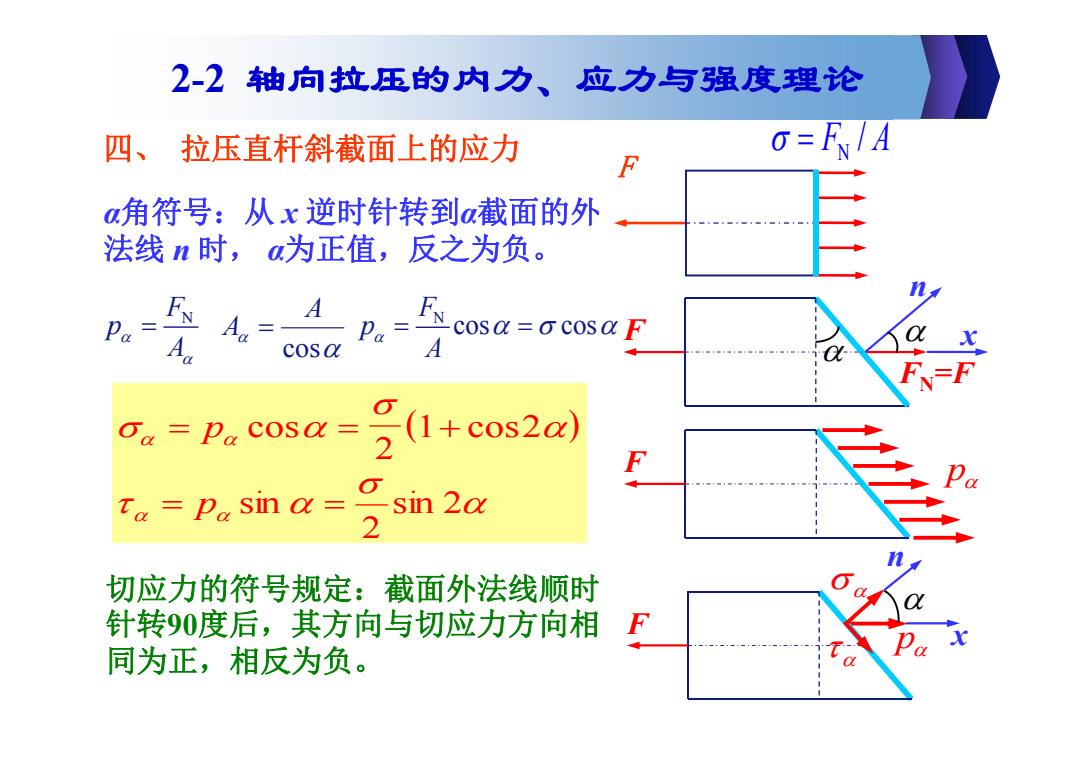
2-2轴向拉压的内力、应力与强度理论 四、拉压直杆斜截面上的应力 =A a角符号：从x逆时针转到α截面的外 法线n时，a为正值，反之为负。 Pa=Aa Aa= Fscosa=a cosa F Pa=A Oa=Pa cosa=2( (1+cos2a) Ta=pa sin a= sin 2a 2 切应力的符号规定：截面外法线顺时 针转90度后，其方向与切应力方向相 同为正，相反为负

F N   F A/ FN=F  n F x  α角符号：从 x 逆时针转到α截面的外 法线 n 时， α为正值，反之为负。 F p FN p A    N cos cos F p A         cosA A  p F      n x          p cos cos  2 1 2       sin 2 2  p sin  切应力的符号规定：截面外法线顺时 针转90度后，其方向与切应力方向相 同为正，相反为负。 2-2 轴向拉压的内力、应力与强度理论 四、 拉压直杆斜截面上的应力

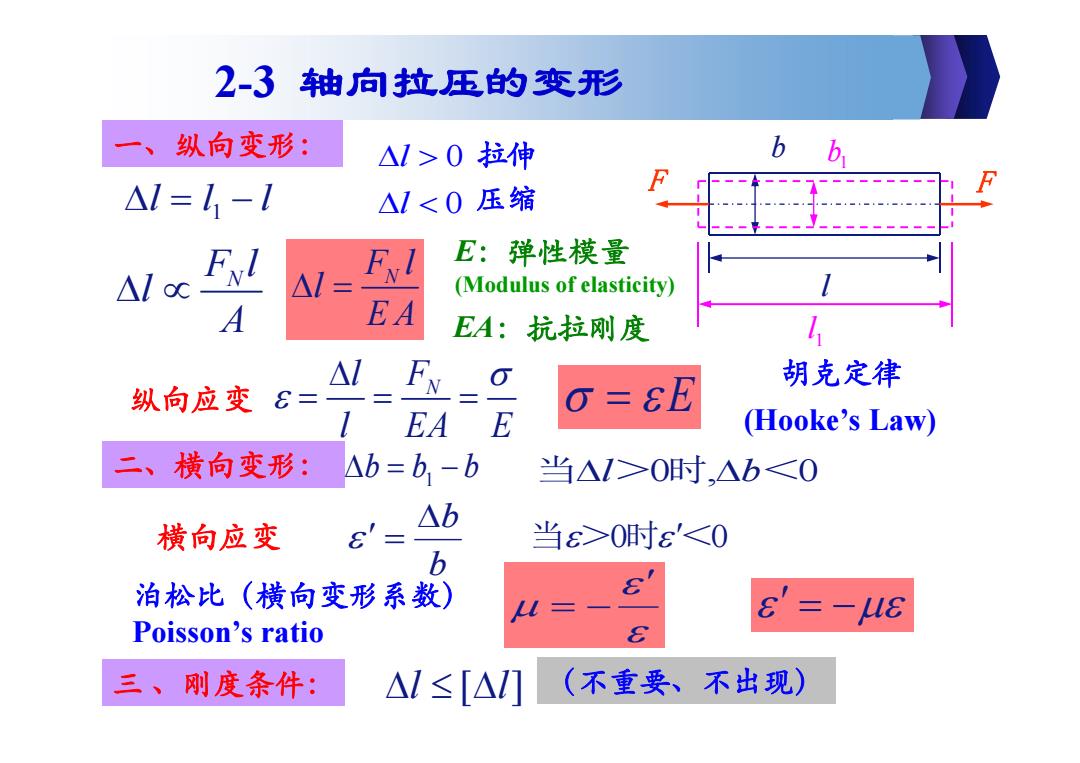
2-3轴向拉压的变形 一、 纵向变形： △1>0拉伸 bb △1=Z-1 △1<0压缩 Ft E:弹性模量 △loc △1= (Modulus of elasticity) A EA EA:抗拉刚度 △ FN 胡克定律 纵向应变8= EA E (Hooke's Law) 二、横向变形： △b=b-b 当△1>0时，△b≤0 △b 横向应变 e' 当8>0时ε'<0 b 泊松比（横向变形系数） El =- Poisson's ratio 三、刚度条件： △1≤[△] (不重要、不出现)

一、纵向变形： F F l b l 1 b1 ll l  1  0 0 l l     F l N l A   E：弹性模量 (Modulus of elasticity) F l N l E A   FN l l EA E         E 胡克定律 (Hooke’s Law) 二、横向变形： bb b  1  当  l ＞ 0 时 ,  b ＜ 0 b  b 横向应变   当 ＞ 0 时＜ 0 泊松比（横向变形系数） Poisson’s ratio          EA：抗拉刚度 2-3 轴向拉压的变形 纵向应变 拉伸 压缩 三 、刚度条件： l l  [ ] （不重要、不出现）

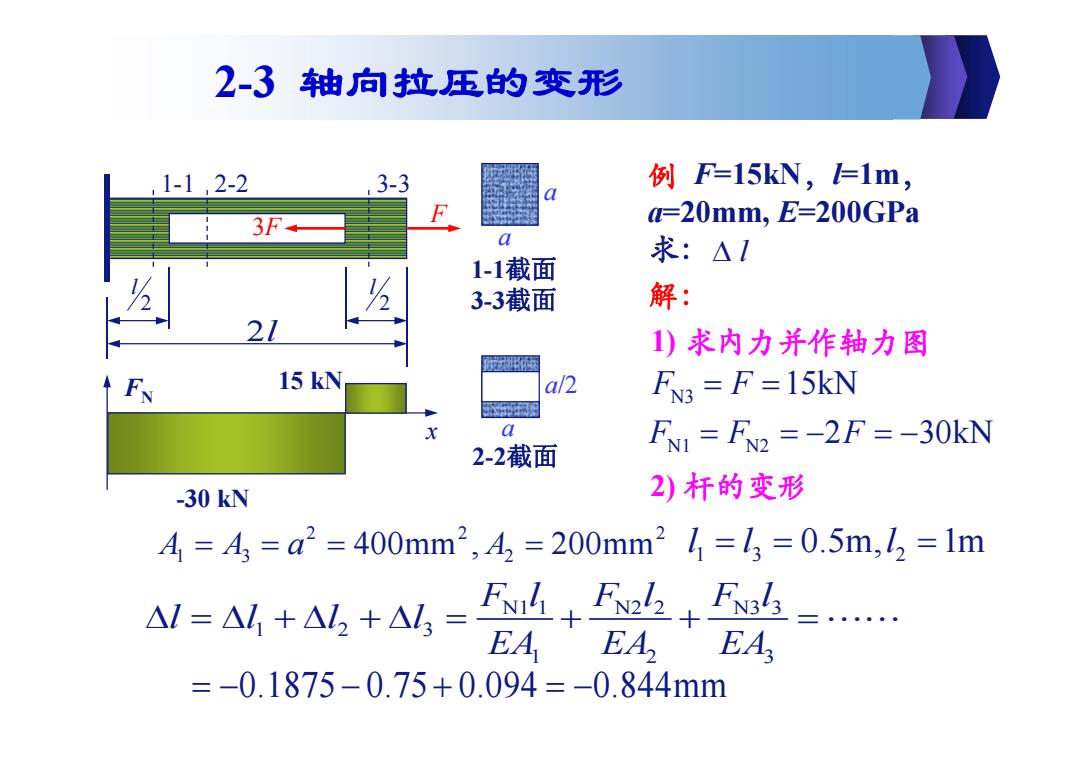
2-3轴向拉压的变形 1-12-2 ,3-3 例F=15kN,=1m, 3F a=20mm,E=200GPa a 求：△1 1-1截面 3-3截面 解： 21 1)求内力并作轴力图 FN 15 kN a/2 FN3 F=15kN a F1=F2=-2F=-30kN 2-2截面 -30kN 2)杆的变形 A=A,=a2=400mm2,A,=200mm21=1,=0.5m,1,=1m A1=AM+A3+△，= Fshl EA EA EA =-0.1875-0.75+0.094=-0.844mm

F l 2 l 2 2l 1-1 2-2 3-3 3F a a 1-1截面 3-3截面 a a/2 2-2截面 例 F=15kN，l=1m， a=20mm, E=200GPa 求： l 解： N1 N2 FF F    2 30kN N3 FN F F  15kN x -30 kN 15 kN 22 2 13 2 AAa A   400mm , 200mm 13 2 ll l    0.5m, 1m N1 1 N2 2 N3 3 123 123 Fl Fl Fl lll l EA EA EA              0.1875 0.75 0.094 0.844mm 1) 求内力并作轴力图 2) 杆的变形 2-3 轴向拉压的变形