2-3轴向拉压的变形 例薄壁圆环直径为D,厚 度为t,圆环内受均匀内压g ,圆环材料的弹性模量为E 。求薄壁圆环的应力与变形 F G gD 解:平衡条件 E= 2t E 2Et 周长的改变:△s=6s= gDs 9πD2 2 2Et 2Et △S _9D2 FN D = 直径的改变:△D= 2 π 2Et
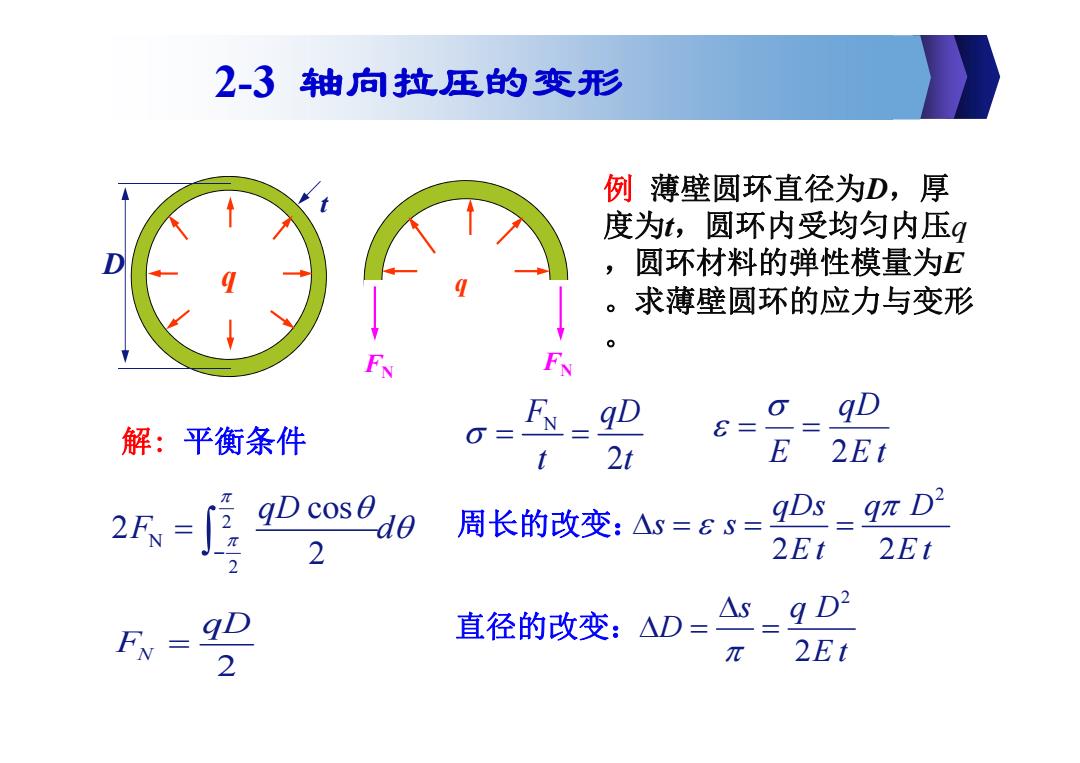
例 薄壁圆环直径为D,厚 度为t,圆环内受均匀内压q ,圆环材料的弹性模量为E 。求薄壁圆环的应力与变形 。 q D t FN FN q 解: 平衡条件 N 2 F qD t t E t qD E 2 2 2 2 qDs q D s s Et Et 2 2 s qD D E t 2 N 2 cos 2 2 qD F d 2 N qD F 周长的改变: 直径的改变: 2-3 轴向拉压的变形
2-3轴向拉压的变形 例AC杆为刚性,BD杆横截面 面积为A,弹性模量为E。求A点 的竖直位移。 D L2 解:求内力 ∑m(C)=0 sin×L-F(L+L2)=0 B A F、 BD F(L+L) ALB ALA sinaxL △LBD EA cosa B △LBD △L4 △LB(L+L2) sin a L 切线代替圆弧,得到新位置 B' 2、向原杆做垂线,得到伸长量
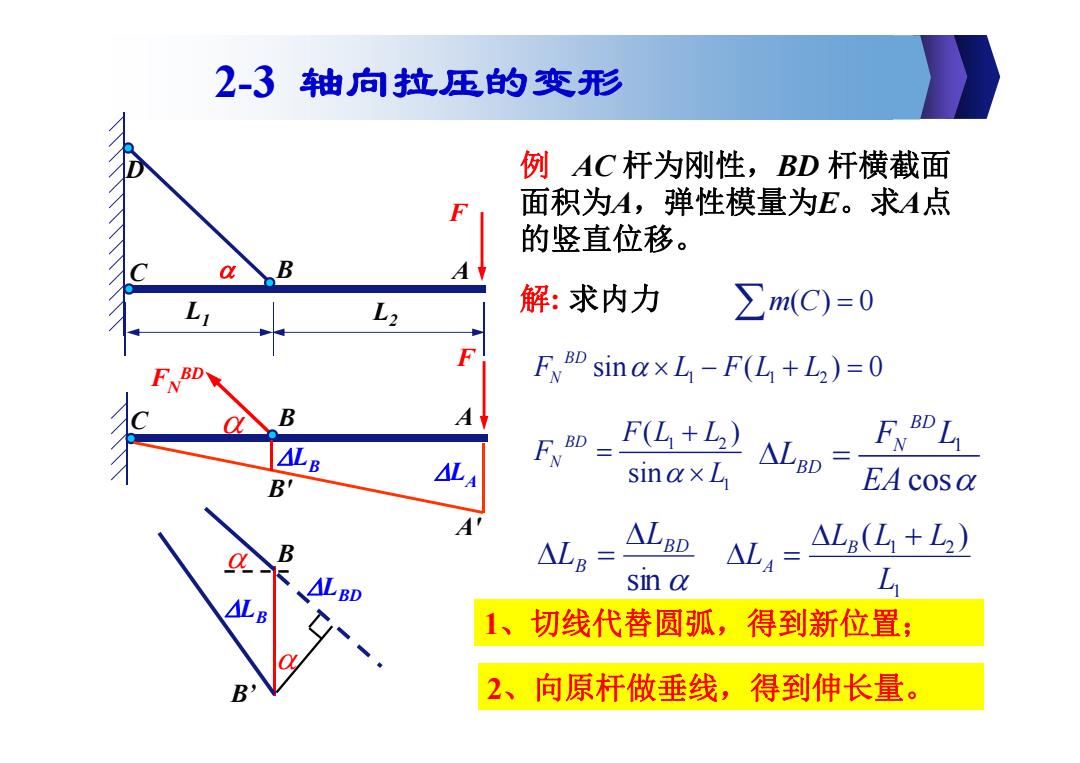
例 AC 杆为刚性,BD 杆横截面 面积为A,弹性模量为E。求A点 的竖直位移。 m(C) 0 1 12 sin ( ) 0 BD F L FL L N 1 2 1 ( ) sin BD N F L L F L sin BD B L L 解: 求内力 1 cos BD N BD F L L EA 1 1 2 ( ) L L L L L B A 1、切线代替圆弧,得到新位置; F C B A FNBD LA LB B' A' LBD LB B B’ 2、向原杆做垂线,得到伸长量。 2-3 轴向拉压的变形 F L1 L2 B A D C

2-5拉压超静定问题 静定结构(Statically determinate structure):所有的未知力均 能由静力平衡方程确定的结构。 超静定结构或静不定结构(Statically indeterminate structure): 仅仅用平衡方程不能求得所有未知力的结构。 ∑F=0:F1=F2 >F,=0:(FN+Fv2)cosa+Fva=F 多余约束:维持平衡所不需要的约束。 超静定次数:未知力数目与独立平衡方程数的差。 多余约束的求解需要补充方程才能确定,补充方 程往往是几何方程(变形协调方程)
Fx 0: F F N1 N2 12 3 0: ( )cos Fy NN N FF F F 静定结构(Statically determinate structure):所有的未知力均 能由静力平衡方程确定的结构。 F FN1 FN3 FN2 F A F 2 超静定结构或静不定结构(Statically indeterminate structure): 仅仅用平衡方程不能求得所有未知力的结构。 2-5 拉压超静定问题 多余约束:维持平衡所不需要的约束。 超静定次数:未知力数目与独立平衡方程数的差。 多余约束的求解需要补充方程才能确定,补充方 程往往是几何方程(变形协调方程)

2-5拉压超静定问题 例求两端固定直杆的约束反力。 EA B 解:解除右端约束,以约束反力代替 平衡方程:1=F+R,FN2=RB 几何方程:△1=△M,+△,=0 B 2 物理方程:△1= EA A= FN2 b EA RB 补充方程: (F+RB)a REb + 二0 EA EA Fb 解得:RB=一 Fa a+b RA= a+b
例 求两端固定直杆的约束反力。 F a b EA EA A B 1 2 , FN BN B FR F R 解: 几何方程: 1 2 1 2 , FN N a Fb l l E A EA 物理方程: 补充方程: 0 ( ) EA R b EA F RB a B 解得: a b Fb RA 平衡方程: 解除右端约束,以约束反力代替 0 R l l1 l2 B A F 1 2 RB F RA a b Fa RB 2-5 拉压超静定问题
2-5拉压超静定问题 例1、2两根直杆的抗拉刚度分别为 E1A1和E2A2,求两杆的内力。 解: 1、判别:为一次超静定 2、假设变形状态,确定内力方向 3、平衡方程:2F2+FN1=2F 4、几何方程:△L2=2△L 5、物理方程:△L,= FNL FN i=1,2 EA C 6、联立求解得:Fw1= 2F 4F FN2=7 B' 4 C2 F
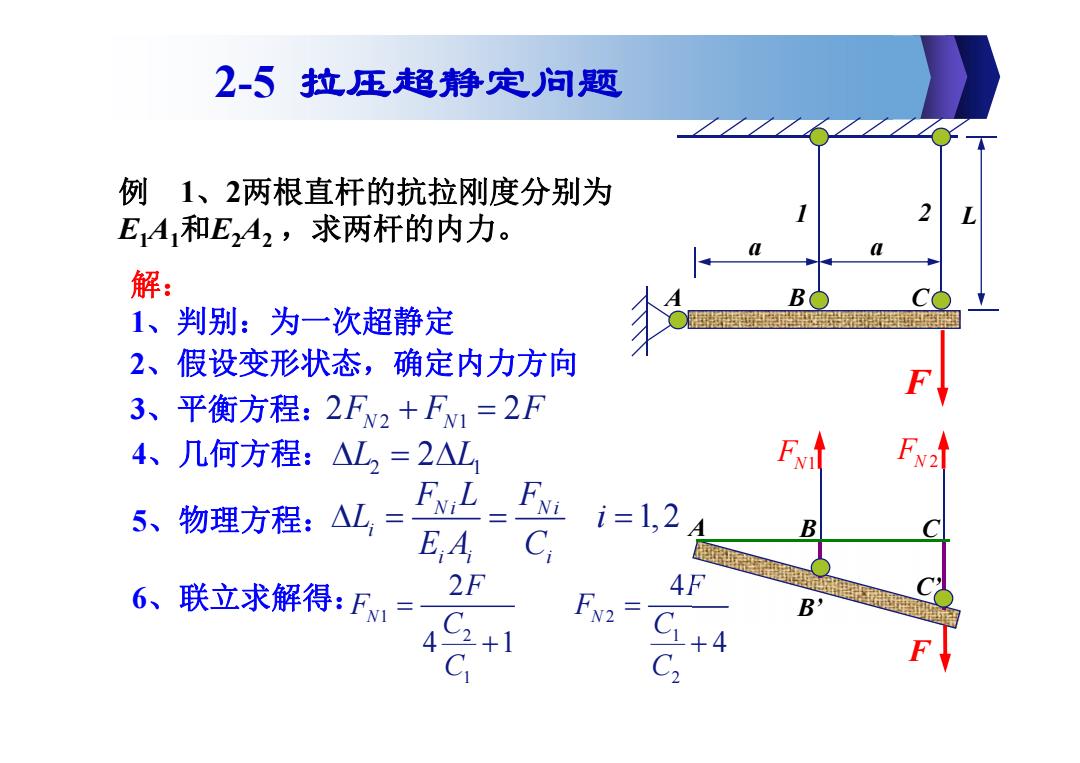
a a 1 2 F L A B C 例 1、2两根直杆的抗拉刚度分别为 E1A1和E2A2 ,求两杆的内力。 解: 1、判别:为一次超静定 2、假设变形状态,确定内力方向 3、平衡方程: 2 1 2 2 FN N F F 4、几何方程: 2 1 L 2L 5、物理方程: 1, 2 Ni Ni i ii i FL F L i EA C 6、联立求解得: 1 2 2 1 1 2 2 4 41 4 N N F F F F C C C C A B C C’ B’ F FN1 FN 2 2-5 拉压超静定问题