《电路》课程教学课件（PPT讲稿）第16章 二端口网络

例1：求Π型电路的Y参数。 02 ●电路的结构和参数为已知， 结束 可直接按定义分析计算。 1' Yu- i i i =Ya+Yp =-Yp Ix. U2=0 Y21= U2=0 12 1⊙ b Y12 =-Yh Vx U1=0 U:-0 U, L Y22= =Yp+Yc 021 U2U=0 2025年4月2日星期三 11

结束 2025年4月2日星期三 11 例1：求P型电路的Y参数。 电路的结构和参数为已知， 可直接按定义分析计算。 Y11 = .I1 . U1 . U2=0 Y21 = .I2 . U1 . U2=0 Y12 = .I1 . U2 . U1=0 Y22 = .I2 . U2 . U1=0 =Ya+Yb = - Yb = - Yb =Yb+Yc 1 1' 2 2' Ya Yb Yc .I2 + - . U2 .I1 . U1=0 1 1' 2 2' Ya Yb Yc .I2 + - . U1 .I1 . U2=0 1 1' 2 2' Ya Yb Yc .I2 .I2 = - Yb

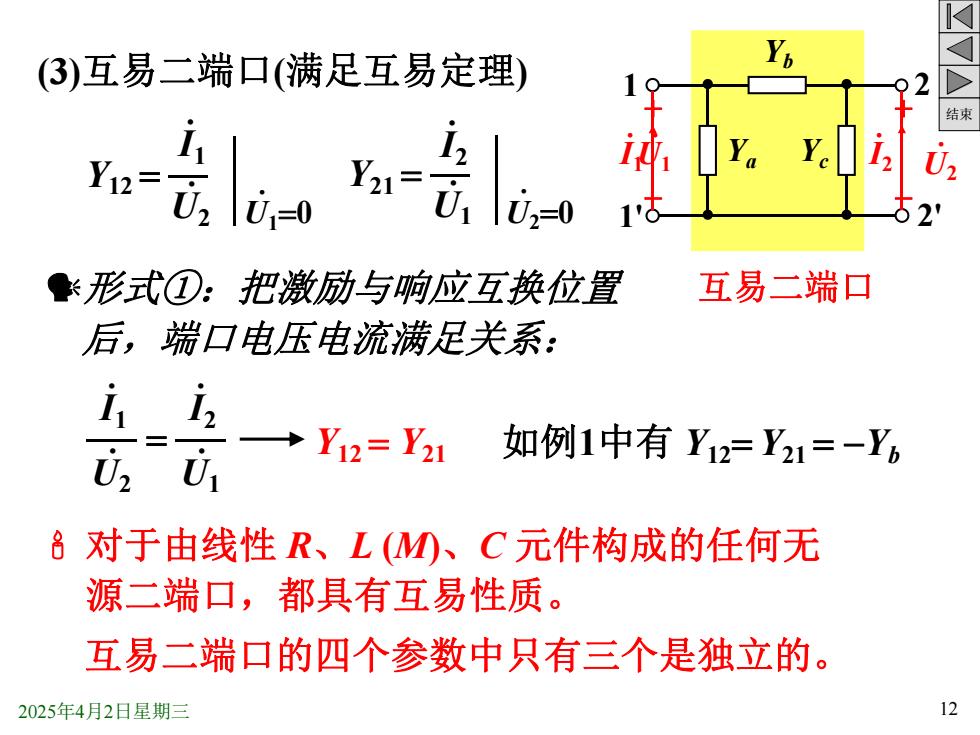
(3)互易二端口（满足互易定理） 结束 Ye Iz U, 2 形式①：把激励与响应互换位置 互易二端口 后，端口电压电流满足关系： ii →Y12=Y21 如例1中有Y12=Y21=-Y6 U2 U 对于由线性R、L(M、C元件构成的任何无 源二端口，都具有互易性质。 互易二端口的四个参数中只有三个是独立的。 2025年4月2日星期三 12

结束 2025年4月2日星期三 12 (3)互易二端口(满足互易定理)  对于由线性 R、L (M)、C 元件构成的任何无 源二端口，都具有互易性质。 互易二端口的四个参数中只有三个是独立的。 Y21 = .I2 . U1 . U2=0 Y12 = .I1 . U2 . U1=0 . U2 .I1 Y12 = Y21 如例1中有 Y12= Y21 = -Yb 1 1' 2 2' Ya Yb Yc 形式①：把激励与响应互换位置 互易二端口 后，端口电压电流满足关系： = . U1 .I2 . U1 + - .I2 .I1 . U2 + -

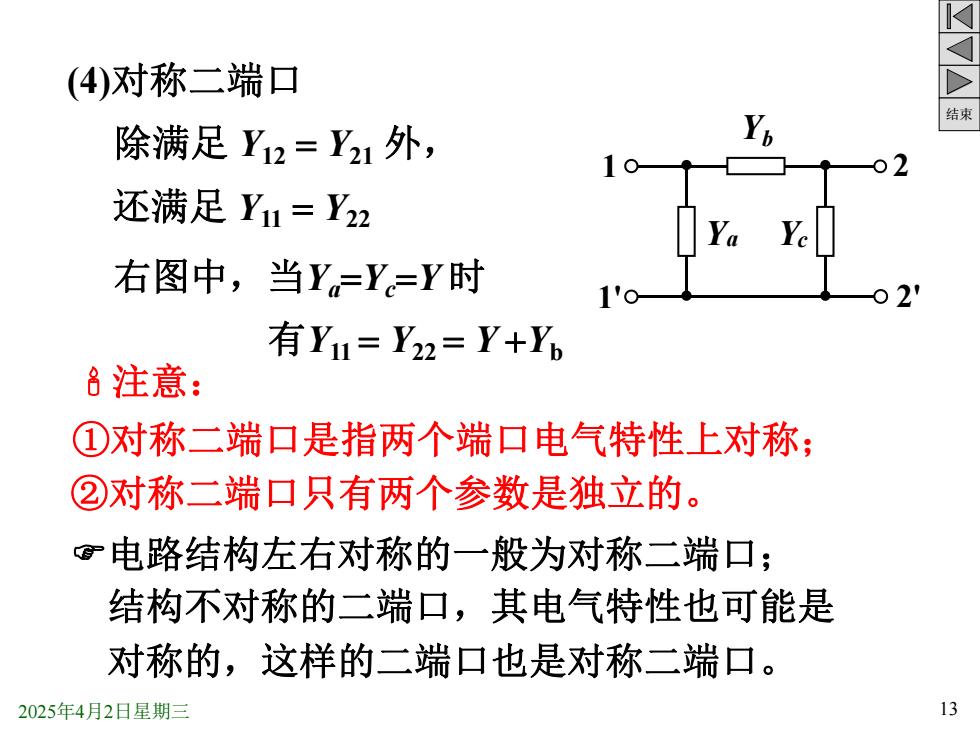
(4)对称二端口 结束 除满足Y12=Y21外， 02 还满足Y1=Y22 Ya Ye 右图中，当Y=Y=Y时 02' 有Y1=Y2=Y+Yb 8注意： ①对称二端口是指两个端口电气特性上对称； ②对称二端口只有两个参数是独立的。 ©电路结构左右对称的一般为对称二端口； 结构不对称的二端口，其电气特性也可能是 对称的，这样的二端口也是对称二端口。 2025年4月2日星期三 13

结束 2025年4月2日星期三 13 (4)对称二端口 电路结构左右对称的一般为对称二端口； 右图中，当Ya =Yc =Y 时  注意： 除满足 Y12 = Y21 外， 还满足 Y11 = Y22 1 1' 2 2' Y Yb Y 有Y11 = Y22 = Y +Yb a c 结构不对称的二端口，其电气特性也可能是 对称的，这样的二端口也是对称二端口。 ①对称二端口是指两个端口电气特性上对称； ②对称二端口只有两个参数是独立的

例2：求图示二 i132 62 端口的Y参数。 解： 19 02 + 结束 0=032 152 U2=0 Yu= i 021 (3/6)+3 1'o 为互易对称二端口 =0.2S 五 =-0.0667S Y21=1 Y2-7 U 2l00 =-0.0667S Y2= .= .1 ,i店+6+1.5 02 1 02 i=-6+313) 2 =- 15 =0.2S 2025年4月2日星期三 14

结束 2025年4月2日星期三 14 例2：求图示二 端口的Y 参数。 1 1' 2 2' 3 3 6 15 + - . U1 .I2 .I1 + - . U2 为互易对称二端口 解： Y11 = .I1 . U1 . U2=0 = (3//6)+3 1 = 0.2S = 0 Y21 = .I2 . U1 . U2=0 Y12 = .I1 . U2 . U1=0 Y22 = .I2 . U2 . U1=0 = = - 0.0667S = 0.2S .I1 . U1 3 1 = -0.0667S - = 0 6+(3//3) .I1= - . U2 2 1 = - 15 . U2 = 15 1 + (6+1.5) 1

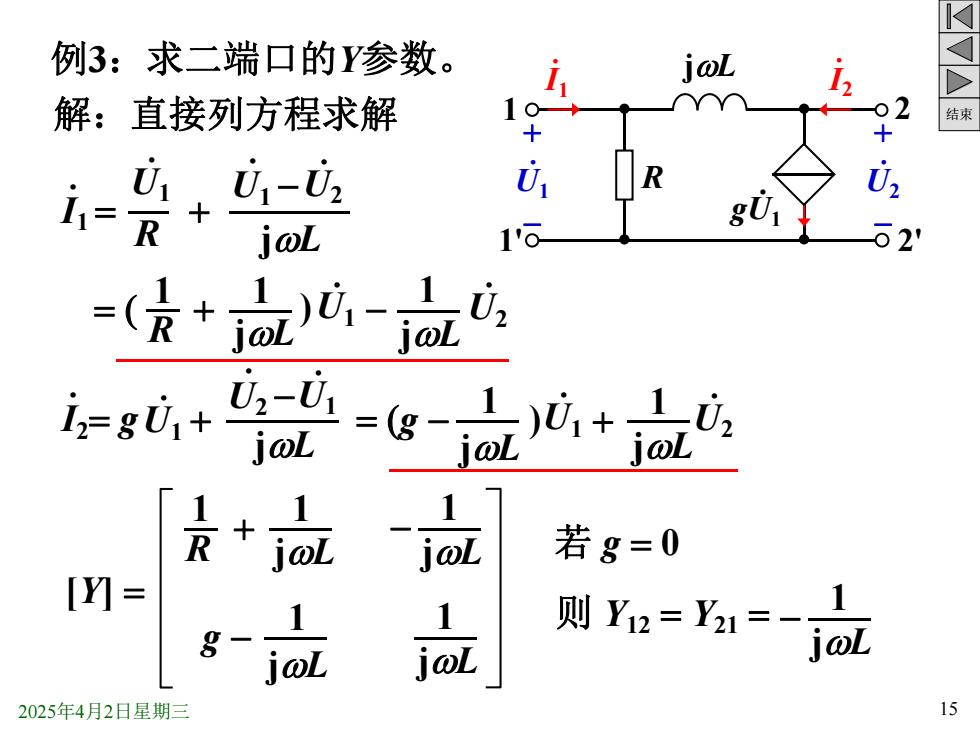
例3：求二端口的Y参数。 joL 解：直接列方程求解 10 结束 i= 01,01-02 1 R joL 1ò 2 -(R )0-02 jol joL U2-U1 joL - jol )01+02 joL L 若g=0 [Y]= 8- i@L 则Ya=1=-j0 2025年4月2日星期三 15

结束 2025年4月2日星期三 15 例3：求二端口的Y参数。 解：直接列方程求解 jL 1 1' 2 2' R + - . U1 .I2 .I1 + - . . U2 gU1 .I1 = R . U1 + . U1 - . U2 jL = ( R + 1 jL 1 ) . U1 jL 1 . U2 .I2= g . U1 + . U2 - . U1 jL = (g - jL 1 ) . U1 jL 1 . U2 R + 1 jL 1 jL 1 - g - jL 1 jL 1 若 g = 0 则 Y12 = Y21 = jL 1 - [Y] = - +