P423例16-2 1① 解:用电流源替代两 结束 个端口电流。 ·由结点电压法 I=(Ya+Y)U-Y U2 62' 写成矩阵形式: I2=-(Y6+g)j+(Y6+Y)U2 Ya+Yo -,]「Ui 比较可求得4个参数: +y Yn Ya YatYi -Yb 通过本例: y-Ya ra ()可采用直接列方 -(Ys+g)Yo+Ye 程法求参数。 (2)含受控源时,不满足互易性质,Y2≠Y1。 2025-4-2 16
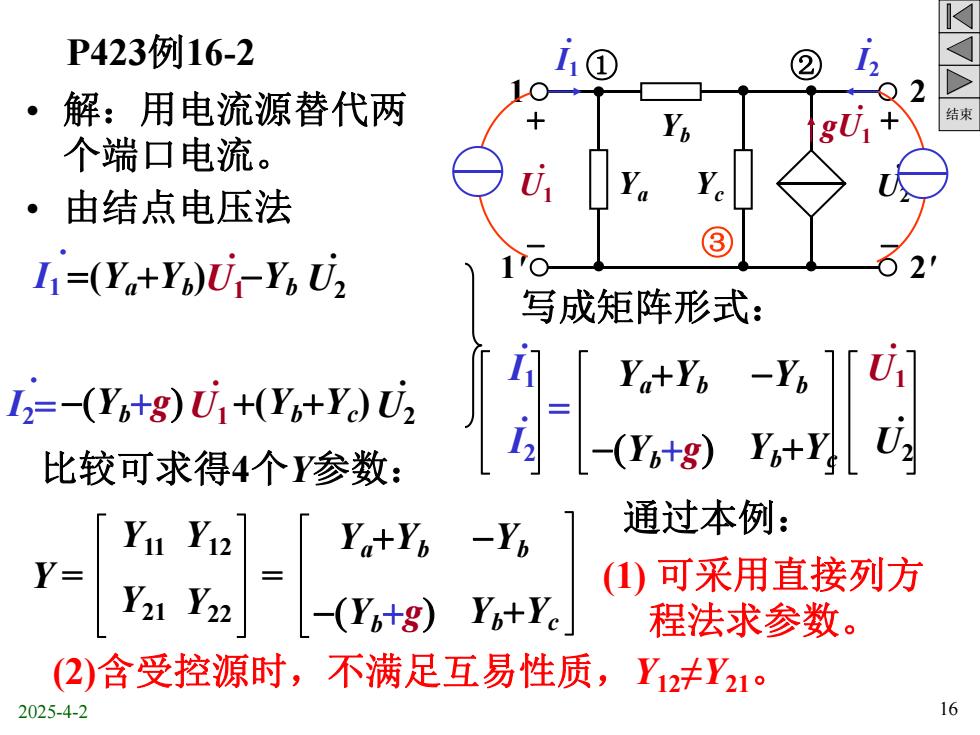
结束 P423例16-2 • 解:用电流源替代两 个端口电流。 • 由结点电压法 Ya Yc Yb + - + - . gU1 . U1 . U2 .I1 .I2 1 1' 2 2' ① ② ③ (Ya+Yb) . U1-Yb . U2 . I1 = -Yb . U1+ (Yb+Yc) . U2 = . I2+ . gU1 . I2= -(Yb+g) . U1+(Yb+Yc) . U2 写成矩阵形式: .I1 .I2 = Ya+Yb -Yb -(Yb+g) Yb+Yc . U1 . U2 比较可求得4个Y参数: Y = Y11 Y21 Y12 Y22 = Ya+Yb -Yb -(Yb+g) Yb+Yc 通过本例: (1) 可采用直接列方 程法求参数。 (2)含受控源时,不满足互易性质,Y12≠Y21。 2025-4-2 16

2.Z(阻抗)参数方程及Z参数 (1)Z参数方程 线性 结束 RLCM 将两个端口各施加一电 +元 受控源 流源,则端口电压可视 为电流源单独作用时产 △y=Y1nY22-Y12Y21 生的电压之和。 (U=Zn in+Zn i -Y2i2 Izint Ar U1-AY 02=Z21i1+Z2i2 ZuI+Zih 也可以由Y参数方程解出 「i1=YuU+Y2U2 △Y li2=Y210+Y2U2 =Z21i1+Z2i2 2025年4月2日星期三 17
结束 2025年4月2日星期三 17 2. Z(阻抗)参数方程及Z参数 将两个端口各施加一电 流源,则端口电压可视 为电流源单独作用时产 生的电压之和。 . U1= Z11 .I1 + Z12 .I2 . U2= Z21 .I1 + Z22 .I2 (1) Z参数方程 .I1 + - + - 线性 RLCM 受控源 . U1 .I2 . U2 .I1 .I2 也可以由Y参数方程解出 .I1 = Y11 . U1+ Y12 . U2 .I2 = Y21 . U1+ Y22 . U2 . U1 = Y Y22 .I1 Y -Y12 .I2 . U2 = Y -Y21 Y Y11 .I1 .I2 Y = Y11 Y22 - Y12 Y21 = Z11 .I1 + Z12 .I2 = Z21 .I1 + Z22 .I2 + +
Z参数的矩阵形式为: 结束 A [ZI=[YH (2)Z参数的物理意义及计算和测定 U 1=0 i20 Z12 i 输入阻抗; + 线性 12=0 V RLCM 2 受控源 Z21= 转移阻抗; 12=0 Z→开路阻抗参数 Z12= U 转移阻抗; 02 输入阻抗。 I1=0 2025年4月2日星期三 18
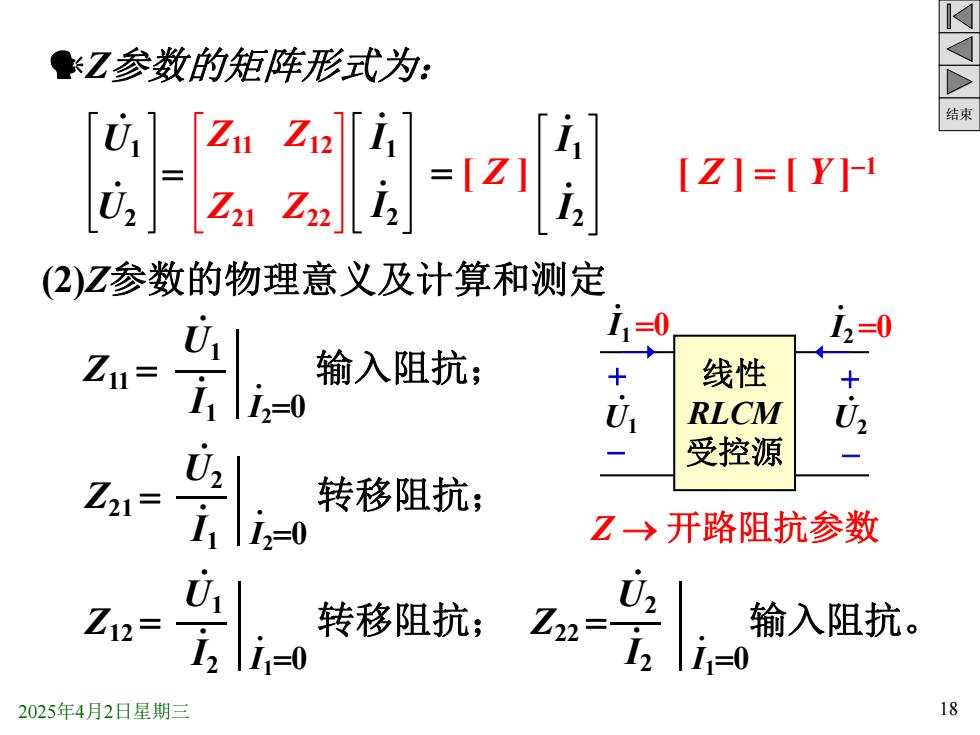
结束 2025年4月2日星期三 18 Z参数的矩阵形式为: (2)Z参数的物理意义及计算和测定 Z11 = . U1 .I1 .I2=0 输入阻抗; . U1 . U2 = Z11 Z12 Z21 Z22 .I1 .I2 = [ Z ] .I1 .I2 [ Z ] = [ Y ]-1 Z21 = . U2 .I1 .I2=0 转移阻抗; .I1 + - + - 线性 RLCM 受控源 . U1 .I2 . U2 .I1 .I2 =0 Z12 = . U1 .I2 .I1=0 转移阻抗; Z22 = . U2 .I2 .I1=0 输入阻抗。 =0 Z 开路阻抗参数

(3)互易性和对称性 互易二端口满足:Z12=Z21 结束 对称二端口还应满足:Z11=Z22 例1:求图中二端口 i=0 Za Zc i2=0 的Z参数。 + V 解法一:按定义 U2 Zu= 01 i-0 Za+Zo Z2= =Z6 Z212 U2 iiz-0 Zo Zn= =Z6+Z。 12i= 2025年4月2日星期三 19
结束 2025年4月2日星期三 19 解法一:按定义 例1:求图中二端口 (3)互易性和对称性 互易二端口满足: Z12 = Z21 对称二端口还应满足: Z11 = Z22 Za Zc Zb + - .I2 . U2 + - . U1 .I1 Z11 = . U1 .I1 .I2=0 Z21 = . U2 .I1 .I2=0 Z12 = . U1 .I2 .I1=0 Z22 = . U2 .I2 .I1=0 = Za + Zb = Zb = Zb = Zb + Zc =0 =0 的Z参数

例1:求图示两端口 结束 的Z参数。 U U g解法二:列KVL方程 U=Zoi+Z (i+i2)(Za+Zn)1+Zn iz U2=Zeiz+Zs (i+iz)Zin+(Zs+Ziz Za+Zo Zo z1=乙。2,+2网 8直接列方程(回路法或结点法)求解比按定义 求解更方便些,特别是网络中含受控源时。 2025年4月2日星期三 20
结束 2025年4月2日星期三 20 例1:求图示两端口 的Z参数。 解法二: Za Zc Zb + - .I2 . U2 + - . U1 .I1 列KVL方程 . U1 = Za .I1 + Zb ( .I1+ .I2) = (Za + Zb ) .I1 + Zb .I2 . U2 = Zc .I2 + Zb ( .I1+ .I2) = Zb .I1+ (Zb + Zc) .I2 Zb Zb [ Z ] = Za + Zb Zb + Zc 直接列方程(回路法或结点法)求解比按定义 求解更方便些,特别是网络中含受控源时