
10 第一章钱性方程组 1.若(1.2)有解,则1=…=n=0.若+1=…=n=0,则可以解出工1工m…, 为其它变元的一次函数 2.设1=…=n=0.当r=n时,由(12)的前r个方程,可依次解出x,n-1,…,1, 解是唯一的.当r<n时,设i{p,2,严},则可取任意值,(1.2)的解不唯一.口 习题 1.证明定理1.1. 2.求解下列线性方程组 2m1+2-2x4=1 1-4r%+24=0 1+2-3=1 1+22-2x3=0 2x2-xg-x4=1 x1+2-xg+x4=0 x1+2x2+2xg-2x4=1 x1+32-3z3-x4=0 x1+2-x+26=1 1+x2-2g+2x6=1 x1-3-x4-x5=1 x2-2xg+x4+2z5=1 (3) 2x1-2x2+xg+x4+2x6=1 x1-xg十x4十x5=1 21+2+x-6=1 (1+2-3-2x4+=1 工1+x2-x3+2x4+x6=1 1十x2+x4=-2 x1+3x2+4r4+5x5=1 2z1+2x3-x4=1 (⑤){21+x2-44+54=1 (6){21+x2-xg-4=0 22++24+46=1 1-2-23-2x4=4 21+3x2+3-x4+46=1 2x2-2+x4=-3 3.证明:当m<n且==…=bm=0时,齐次线性方程组(11)必有非零解
10 第一章 线性方程组 1. 若 (1.2) 有解,则 b ′ r+1 = · · · = b ′ m = 0.若 b ′ r+1 = · · · = b ′ m = 0,则可以解出 xp1 , xp2 , · · · , xpr 为其它变元的一次函数. 2. 设 b ′ r+1 = · · · = b ′ m = 0.当 r = n 时,由 (1.2) 的前 r 个方程,可依次解出 xn, xn−1, · · · , x1, 解是唯一的.当 r < n 时,设 i ∈ { / p1, p2, · · · , pr},则 xi 可取任意值,(1.2) 的解不唯一. 习题 1. 证明定理 1.1. 2. 求解下列线性方程组. (1) 2x1 + x2 − 2x4 = 1 x1 + x2 − x3 = 1 2x2 − x3 − x4 = 1 x1 + 2x2 + 2x3 − 2x4 = 1 (2) x1 − 4x3 + 2x4 = 0 x1 + 2x2 − 2x3 = 0 x1 + x2 − x3 + x4 = 0 x1 + 3x2 − 3x3 − x4 = 0 (3) x1 + x2 − x3 + 2x5 = 1 x1 − x3 − x4 − x5 = 1 2x1 − 2x2 + x3 + x4 + 2x5 = 1 2x1 + x2 + x3 − x5 = 1 (4) x1 + x2 − 2x3 + 2x5 = 1 x2 − 2x3 + x4 + 2x5 = 1 x1 − x3 + x4 + x5 = 1 x1 + x2 − x3 − 2x4 + x5 = 1 (5) x1 + x2 − x3 + 2x4 + x5 = 1 x1 + 3x2 + 4x4 + 5x5 = 1 2x1 + x2 − 4x3 + 5x4 = 1 2x2 + x3 + 2x4 + 4x5 = 1 2x1 + 3x2 + 3x3 − x4 + 4x5 = 1 (6) x1 + x2 + x4 = −2 2x1 + 2x3 − x4 = 1 2x1 + x2 − x3 − x4 = 0 x1 − 2x2 − 2x3 − 2x4 = 4 2x2 − 2x3 + x4 = −3 3. 证明:当 m < n 且 b1 = b2 = · · · = bm = 0 时,齐次线性方程组 (1.1) 必有非零解.

S1.2矩阵表示 1.2矩阵表示 在对线性方程组施行初等变换的时候,我们注意到每个方程的左端都是数与字母的乘积之和的 形式,只需要对未知数的系数进行操作:并且方程的个数、未知数的个数、未知数的顺序均保持不 变.因此,我们可以隐去未知数和运算符号,用一个m行n+1列的矩形表格 012 01n 121 02n (1.3) 来表示线性方程组(11),把对于线性方程组的操作转化为对于矩形表格的操作,《九章算术·方程》 中就记拔若这样的解法:用算筹把线性方程组的系数和常数项排成长方形阵,燃后用加减消元法求 解.秦九韶四的《数书九章》(成书于1247年)中则用互乘相消法和代入法求解线性方程组 例1.2.回今有上禾三秉、中禾二秉、下禾一秉,实三十九斗:上禾二秉、中禾三兼、下禾一秉,实 三十四斗:上禾一兼、中禾二兼、下禾三秉,实二十六斗.问上、中、下禾实一秉各几何?答曰:上 禾一秉,九斗、四分斗之一:中禾一秉,四斗、四分斗之一:下禾一秉,二斗、四分斗之三. 方程术曰:置上禾三秉,中禾二秉,下禾一秉,实三十九斗,于右方.中、左行列如右方.以右 行上禾遍乘中行而以直除。又乘其次,亦以直除。然以中行中禾不尽者遍乘左行而以直除.左方丁 禾不尽者,上为法,下为实。实即下禾之实.求中禾,以法乘中行下实,而除下禾之实。余如中禾 秉数而一,即中禾之实,求上禾亦以法乘右行下实,而除下禾、中禾之实,余如上禾秉数而一,即 上禾之实。实皆如法,各得一斗 下面,我们来学习古人的“方程术”.用现代数学的语言来说,原问题等价于求解线性方程组 3x+2y+=39 2x+3y+2=34 x+2u+32=26 首先,把线性方程组的系数按照古人的书写顺序(从上到下,从右到左,行是竖直方向)排成数表。 数表逆时针旋转90°,即为线性方程组的增广矩阵。 左行中行右行 上禾1 23 中禾 2 2 下禾3 1 1 实263439 然后,用(右行,上禾)位置的数3遍乘中行的每个元素,再利用右行对中行消元,得 123 /1631 /103 311 33i 263439/ 2610239/ 262439
§1.2 矩阵表示 11 §1.2 矩阵表示 在对线性方程组施行初等变换的时候,我们注意到每个方程的左端都是数与字母的乘积之和的 形式,只需要对未知数的系数进行操作;并且方程的个数、未知数的个数、未知数的顺序均保持不 变.因此,我们可以隐去未知数和运算符号,用一个 m 行 n + 1 列的矩形表格 M = a11 a12 · · · a1n b1 a21 a22 · · · a2n b2 . . . . . . · · · . . . . . . am1 am2 · · · amn bm (1.3) 来表示线性方程组 (1.1),把对于线性方程组的操作转化为对于矩形表格的操作.《九章算术 · 方程》 中就记载着这样的解法:用算筹把线性方程组的系数和常数项排成长方形阵,然后用加减消元法求 解.秦九韶[1]的《数书九章》(成书于 1247 年)中则用互乘相消法和代入法求解线性方程组. 例 1.2. [2]今有上禾三秉、中禾二秉、下禾一秉,实三十九斗;上禾二秉、中禾三秉、下禾一秉,实 三十四斗;上禾一秉、中禾二秉、下禾三秉,实二十六斗.问上、中、下禾实一秉各几何?答曰:上 禾一秉,九斗、四分斗之一;中禾一秉,四斗、四分斗之一;下禾一秉,二斗、四分斗之三. 方程术曰:置上禾三秉,中禾二秉,下禾一秉,实三十九斗,于右方.中、左行列如右方.以右 行上禾遍乘中行而以直除.又乘其次,亦以直除.然以中行中禾不尽者遍乘左行而以直除.左方下 禾不尽者,上为法,下为实.实即下禾之实.求中禾,以法乘中行下实,而除下禾之实.余如中禾 秉数而一,即中禾之实.求上禾亦以法乘右行下实,而除下禾、中禾之实.余如上禾秉数而一,即 上禾之实.实皆如法,各得一斗. 下面,我们来学习古人的“方程术”.用现代数学的语言来说,原问题等价于求解线性方程组 3x + 2y + z = 39 2x + 3y + z = 34 x + 2y + 3z = 26 首先,把线性方程组的系数按照古人的书写顺序 (从上到下,从右到左,行是竖直方向) 排成数表. 数表逆时针旋转 90◦,即为线性方程组的增广矩阵. 左行 中行 右行 上禾 1 2 3 中禾 2 3 2 下禾 3 1 1 实 26 34 39 然后,用 (右行, 上禾) 位置的数 3 遍乘中行的每个元素,再利用右行对中行消元,得 1 2 3 2 3 2 3 1 1 26 34 39 → 1 6 3 2 9 2 3 3 1 26 102 39 → 1 0 3 2 5 2 3 1 1 26 24 39 . [1]秦九韶,约 1202–1261,南宋著名数学家,四川安岳人. [2]《九章算术》第 8 章《方程》第 1 题.

12 第一章钱性方程组 再对左行作同样的处理,得 262439/ 782439 20420 然后,用(中行,中禾)位置的数5遍乘左行的每个元素,再利用中行对左行消元,得 392439/ 992439 (左行,下禾)位置的数36称为法,(左行,实)位置的数99称为下禾之实.即36秉下禾实99斗, 透亭 =333为上 禾之实.即36秉上禾实333斗. 因此,果上、中,下不之安的斗数分是罗=9行密=号器=号 0 古人的做法几平就是Ga器消元法,先把系数矩阵初等变换成上三角形,再依次回代求解未知 数 在求解过程中,古人始终把运算限制在整数范围内,只是在最后才以分数的形式给出答案究 其原因,古人使用算筹来表示数字,追求计算过程的简洁和精确,与其使用分数,不如先通分,而 后始终在整数范用内运算.事实上,《九章算术》的第一章《方田》中就已经给出了分数的加、减 乘、除、通分、约分运算.分母称为“法”,分子称为“实”例1.2中的“实”,有时指的是“农作 物的收成”,有时指的是“分数的分子”,读者需仔细区分 定义12.(1.3)式中的矩形表格M称为线性方程组(1.1)的增广矩阵.别去M的最后一列得到的 m行n列的矩形表格称为线性方程组(1.1)的系数矩阵。M的第i行从左至右排成的数组,称为 M的第i个行向量.M的第j列从上至下排成的数组,称为M的第j个列向量. 全矩阵的元素并不仅限于数,也可以是含有未知数和字母的代数表达式。 定义1.3.由数域F中的n个数构成的数组=(1,2,…,)称为数域罩上的n维数组向量 简称n维向量,数域丽上所有n维数组向量的集合记作F,元素都是0的向量称为零向量,记作 0.第i个元素是1、其它元素都是0的向量称为第i个标准单位向量,记作e, 设=(1,欢,·,)∈m,入∈R.两个向量的加法运算定义为 工+y=(1+,2+2,…,n+n) 数与向量的数乘运算定义为 Az=(AD1,A2,·,Azn)
12 第一章 线性方程组 再对左行作同样的处理,得 1 0 3 2 5 2 3 1 1 26 24 39 → 3 0 3 6 5 2 9 1 1 78 24 39 → 0 0 3 4 5 2 8 1 1 39 24 39 . 然后,用 (中行, 中禾) 位置的数 5 遍乘左行的每个元素,再利用中行对左行消元,得 0 0 3 4 5 2 8 1 1 39 24 39 → 0 0 3 20 5 2 40 1 1 195 24 39 → 0 0 3 0 5 2 36 1 1 99 24 39 . (左行, 下禾) 位置的数 36 称为法,(左行, 实) 位置的数 99 称为下禾之实.即 36 秉下禾实 99 斗. 下面计算中禾.已知 5 秉中禾、1 秉下禾实 24 斗.用 36 乘 (中行, 实) 位置处的数 24,减去 下禾之实,再除以中禾秉数 5,所得数 36 × 24 − 99 5 = 153 为中禾之实.即 36 秉中禾实 153 斗. 对于上禾,已知 3 秉上禾、2 秉中禾、1 秉下禾实 39 斗.用 36 乘 (右行, 实) 位置处的数 39, 减去下禾之实与 2 倍的中禾之实,再除以上禾秉数 3,所得数 36 × 39 − 99 − 2 × 153 3 = 333 为上 禾之实.即 36 秉上禾实 333 斗. 因此,1 秉上、中、下禾之实的斗数分别是 333 36 = 9 1 4 , 153 36 = 41 4 , 99 36 = 2 3 4 . 古人的做法几乎就是 Gauss 消元法,先把系数矩阵初等变换成上三角形,再依次回代求解未知 数.在求解过程中,古人始终把运算限制在整数范围内,只是在最后才以分数的形式给出答案.究 其原因,古人使用算筹来表示数字,追求计算过程的简洁和精确,与其使用分数,不如先通分,而 后始终在整数范围内运算.事实上,《九章算术》的第一章《方田》中就已经给出了分数的加、减、 乘、除、通分、约分运算.分母称为“法”,分子称为“实”.例 1.2 中的“实”,有时指的是“农作 物的收成”,有时指的是“分数的分子”,读者需仔细区分. 定义 1.2. (1.3) 式中的矩形表格 M 称为线性方程组 (1.1) 的增广矩阵.删去 M 的最后一列得到的 m 行 n 列的矩形表格称为线性方程组 (1.1) 的系数矩阵.M 的第 i 行从左至右排成的数组,称为 M 的第 i 个行向量.M 的第 j 列从上至下排成的数组,称为 M 的第 j 个列向量. 矩阵的元素并不仅限于数,也可以是含有未知数和字母的代数表达式. 定义 1.3. 由数域 F 中的 n 个数构成的数组 x = (x1, x2, · · · , xn) 称为数域 F 上的 n 维数组向量, 简称 n 维向量.数域 F 上所有 n 维数组向量的集合记作 F n.元素都是 0 的向量称为零向量,记作 0.第 i 个元素是 1、其它元素都是 0 的向量称为第 i 个标准单位向量,记作 ei. 设 y = (y1, y2, · · · , yn) ∈ F n,λ ∈ F.两个向量的加法运算定义为 x + y = (x1 + y1, x2 + y2, · · · , xn + yn), 数与向量的数乘运算定义为 λx = (λx1, λx2, · · · , λxn)

S12矩阵表示 13 显然,向量的加法和数乘运算是数的加法和乘法运算的推广,类似地,可定义两个向量的减法运算 E一割=(E1一1,E2一2:···,工n一n 和线性组合运算 证+=(A1+1,2+,…,A江n+n) 并推广为多个向量a1,a2,·,,∈Pm的线性组合运算 X1a1+X202+…+Xk0w 其中4,1,2,…,keF 以下是对于线性方程组(1.1)的两种常见看法. 1.定义两个n维向量x=(c1,2…,)和y=(1,2,,%)的数量积运算为 卫·=工1班+x2欢+…+nn 记n维向量a=(a,a2,…,an).线性方程组(1.1)可以看作是: 。求向量x=(1,2,…,工n)使得a王=,发=1,2,m. 2.记m维向量月=(aa2,am,b=(,2,…,bn.线性方程组(1.1)还可以看作是: 。求线性组合的系数1,2,…,n使得1十x22+…十xnBn=b. 定理14.数组向量的加法和数乘运算具有下列性质. (A1)(x+)+z=x+(y+2) (A2)x+=y+E A3)r+0=0+E=x (A4)x+(-x)=(-x)+x=0 (M1)()z=X() M2)1r= (D1)A(红+)=r+Aw (D2)(入+4)x=λx+x 其中x,,z∈m,入,μ∈F. 线性方程组(1.1)与矩阵M之间存在一一对应关系.方程a11+a22+…+mxn=与 :)一一对应,方程的常数倍对应于行向量的数乘运算,两个方程之和对应 下间的如法运堂对于线性方问作初等衣换的随元是,可以我为对库酸 行向量作初等变换,把M化为阶梯形的矩阵 M'= drp…dn 女 其中M?中空白处的元素都是0
§1.2 矩阵表示 13 显然,向量的加法和数乘运算是数的加法和乘法运算的推广.类似地,可定义两个向量的减法运算 x − y = (x1 − y1, x2 − y2, · · · , xn − yn), 和线性组合运算 λx + µy = (λx1 + µy1, λx2 + µy2, · · · , λxn + µyn), 并推广为多个向量 α1, α2, · · · , αk ∈ F n 的线性组合运算 λ1α1 + λ2α2 + · · · + λkαk 其中 µ, λ1, λ2, · · · , λk ∈ F. 以下是对于线性方程组 (1.1) 的两种常见看法. 1. 定义两个 n 维向量 x = (x1, x2, · · · , xn) 和 y = (y1, y2, · · · , yn) 的数量积运算为 x · y = x1y1 + x2y2 + · · · + xnyn. 记 n 维向量 αi = (ai1, ai2, · · · , ain).线性方程组 (1.1) 可以看作是: • 求向量 x = (x1, x2, · · · , xn) 使得 αi · x = bi,∀i = 1, 2, · · · , m. 2. 记 m 维向量 βj = (a1j , a2j , · · · , amj ),b = (b1, b2, · · · , bm).线性方程组 (1.1) 还可以看作是: • 求线性组合的系数 x1, x2, · · · , xn 使得 x1β1 + x2β2 + · · · + xnβn = b. 定理 1.4. 数组向量的加法和数乘运算具有下列性质. (A1) (x + y) + z = x + (y + z) (A2) x + y = y + x (A3) x + 0 = 0 + x = x (A4) x + (−x) = (−x) + x = 0 (M1) (λµ)x = λ(µx) (M2) 1x = x (D1) λ(x + y) = λx + λy (D2) (λ + µ)x = λx + µx 其中 x, y, z ∈ F n,λ, µ ∈ F. 线性方程组 (1.1) 与矩阵 M 之间存在一一对应关系.方程 ai1x1 + ai2x2 + · · · + ainxn = bi 与 行向量 (ai1, ai2, · · · , ain, bi) 一一对应,方程的常数倍对应于行向量的数乘运算,两个方程之和对应 于两个行向量的加法运算.对于线性方程组 (1.1) 作初等变换的消元过程,可以表示为对矩阵 M 的 行向量作初等变换,把 M 化为阶梯形的矩阵 M′ = a ′ 1p1 · · · · · · · · · · · · · · · · · · a ′ 1n b ′ 1 a ′ 2p2 · · · · · · · · · · · · a ′ 2n b ′ 2 · · · · · · · · · . . . . . . a ′ rpr · · · a ′ rn b ′ r b ′ r+1 . . . b ′ m 其中 M′ 中空白处的元素都是 0.
14 第一章钱性方程组 例1.3.用矩阵方法求解例1.1. 解答。 /01 -10-1Y /1-200 -200-4 -200-4 交换①.回, 01-10 01-10-1 3-201- 3-201 _7 8 04015 8号 1 3 0 3 13 12 -2 00-4 1 -2 0 0 -4 1-200-4 0 0 0=-2回 01 -10- ③-③ 00 419 00419 00408 00 8319/ 0001 1 0001 1 -2 00 4 1 -200 /1000-2 0 -10 ②+=®01001 ①+=2 0100 00 10 2 00102 00102 00011 00011 00011 上式最后一个矩阵的最后一列即为方程组的解,(任1,x2,正3,x4)=(-2,1,2,1). 习题 1.证明定理1.4. 2.用矩阵方法求解$11习题2. 3.设A(1,0),B(0,2),C(3,3).求△ABC的外接圆方程. 4.设A(L,0,),B(0,2,0),C(0,0,3).求△ABC的外接圆方程. 5.求满足f)=f2)=f3)=1,f(-1)=f(-2)=f(-3)=-1的所有多项式f) 6.求满是f)=P)="()=1,f(-1)=(-1)=f"(-1)=-1的所有多项式f(x) 7.当入取何值时,如下线性方程组有解?有唯一解?并求其所有解 Ar1+2+x4=1 +2+x=1 购+A+4=1 21+z+A4=1 8.当α,b取何值时,如下线性方程组有解?有唯一解?并求其所有解 [ar+z2+z3+=0 2x1-x2+2x3+3x4=b 2x1+x2-xg+2x4=1 2++24=1 2+23+3r4=2
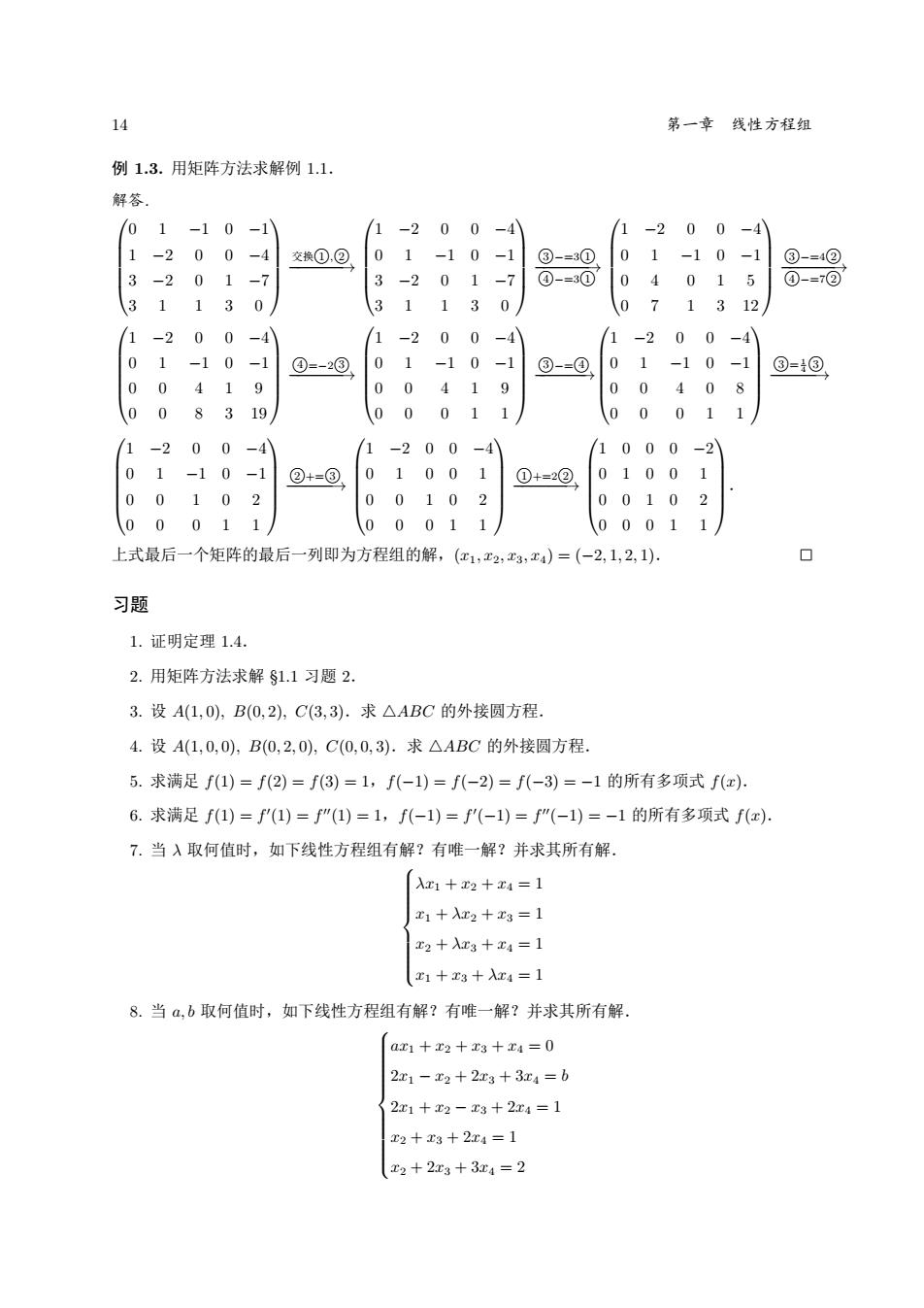
14 第一章 线性方程组 例 1.3. 用矩阵方法求解例 1.1. 解答. 0 1 −1 0 −1 1 −2 0 0 −4 3 −2 0 1 −7 3 1 1 3 0 交换⃝1 ,⃝2 −−−−−−→ 1 −2 0 0 −4 0 1 −1 0 −1 3 −2 0 1 −7 3 1 1 3 0 ⃝3 −=3⃝1 −−−−−−→ ⃝4 −=3⃝1 1 −2 0 0 −4 0 1 −1 0 −1 0 4 0 1 5 0 7 1 3 12 ⃝3 −=4⃝2 −−−−−−→ ⃝4 −=7⃝2 1 −2 0 0 −4 0 1 −1 0 −1 0 0 4 1 9 0 0 8 3 19 ⃝4 =−2⃝3 −−−−−−→ 1 −2 0 0 −4 0 1 −1 0 −1 0 0 4 1 9 0 0 0 1 1 ⃝3 −=⃝4 −−−−−−→ 1 −2 0 0 −4 0 1 −1 0 −1 0 0 4 0 8 0 0 0 1 1 ⃝3 = 1 4⃝3 −−−−−→ 1 −2 0 0 −4 0 1 −1 0 −1 0 0 1 0 2 0 0 0 1 1 ⃝2 +=⃝3 −−−−−→ 1 −2 0 0 −4 0 1 0 0 1 0 0 1 0 2 0 0 0 1 1 ⃝1 +=2⃝2 −−−−−−→ 1 0 0 0 −2 0 1 0 0 1 0 0 1 0 2 0 0 0 1 1 . 上式最后一个矩阵的最后一列即为方程组的解,(x1, x2, x3, x4) = (−2, 1, 2, 1). 习题 1. 证明定理 1.4. 2. 用矩阵方法求解 §1.1 习题 2. 3. 设 A(1, 0), B(0, 2), C(3, 3).求 4ABC 的外接圆方程. 4. 设 A(1, 0, 0), B(0, 2, 0), C(0, 0, 3).求 4ABC 的外接圆方程. 5. 求满足 f(1) = f(2) = f(3) = 1,f(−1) = f(−2) = f(−3) = −1 的所有多项式 f(x). 6. 求满足 f(1) = f ′ (1) = f ′′(1) = 1,f(−1) = f ′ (−1) = f ′′(−1) = −1 的所有多项式 f(x). 7. 当 λ 取何值时,如下线性方程组有解?有唯一解?并求其所有解. λx1 + x2 + x4 = 1 x1 + λx2 + x3 = 1 x2 + λx3 + x4 = 1 x1 + x3 + λx4 = 1 8. 当 a, b 取何值时,如下线性方程组有解?有唯一解?并求其所有解. ax1 + x2 + x3 + x4 = 0 2x1 − x2 + 2x3 + 3x4 = b 2x1 + x2 − x3 + 2x4 = 1 x2 + x3 + 2x4 = 1 x2 + 2x3 + 3x4 = 2