
N!求极值T=TIN!将上式取对数,并用Stirling公式展开Int = In N!-in N,!=NInN-N-ZN,InN,+ZN,再用Lagrange乘因子法,求得最概然的分布为:N, = eα+βei式中 α 和 β 是Lagrange乘因子法中引进的待定因子
将上式取对数,并用Stirling公式展开 ! !i i N t N = 求极值 ln ln ! ln !i t N N = − = − − + N N N N N N ln ln i i i 再用Lagrange乘因子法,求得最概然的分布为: 式中 和 是Lagrange乘因子法中引进的待定因子。 * i N e i + =
值的推导α,βN, = eα+βei先求 αBeiZea=Ne所以已知ZN, = NNeBe或或>α = ln N- lnOebeZiNeBe,N.-ebsM最概然分布公式中已消去了α
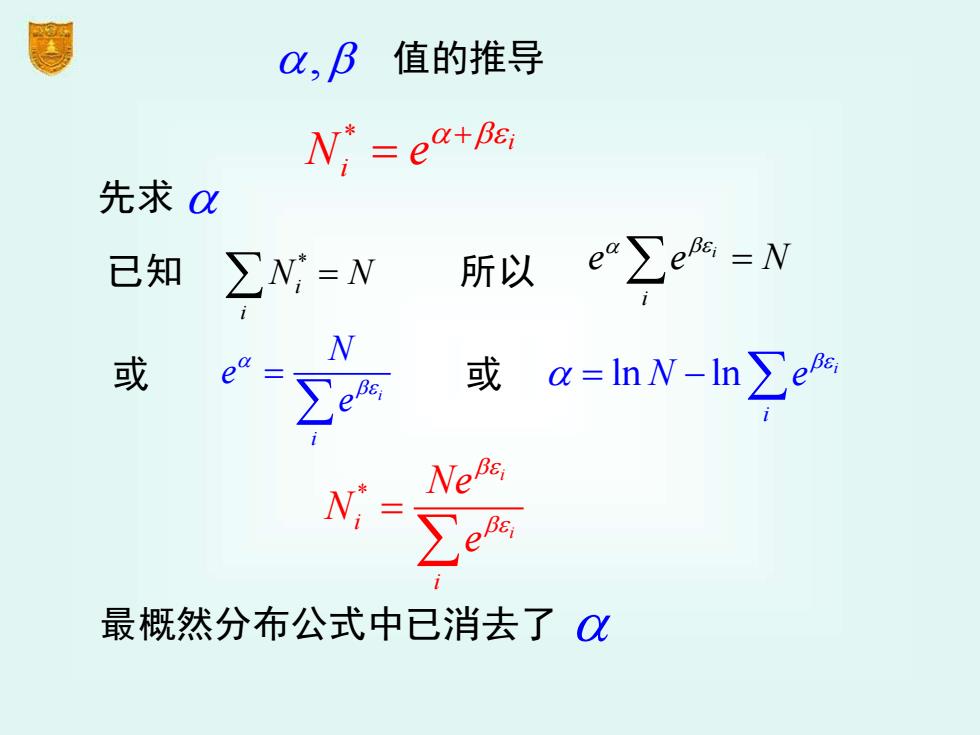
* i N e i + = * i i i i Ne N e = 先求 , 值的推导 已知 * i i N N= 所以 i i e e N = 或 i i N e e = 或 ln ln i i N e = − 最概然分布公式中已消去了

值的推导α,β再求β已知S=klnQ=klnt.Intm = NInN-N-ZN, InN, +ZN,代入得S=kNInN-N-ZN, InN +ZN,=[NInN-Z,In,(N; =N)(N, = ea+βen)= k[N In N-N, (α+β,)(EN, =N; ZN;s,=U)= k[NIn N-αN- βU]= kN In eBei - kβU(α=ln N-ln ec)
, 值的推导 已知 m S k k t = = ln ln 代入得 * * * m ln ln ln i i i t N N N N N N = − − + * * * ln ln i i i i i S k N N N N N N = − − + 再求 ( ) * * * ln ln i i i = − = k N N N N N N ( ) ( ) * * ln i i i i k N N N N e + = − + = ( ) * * ln ; i i i = − − = = k N N N U N N N U ln ln ln ( ) i i kN e k U N e = − = −

值的推导α,βeBei - kβUS = kN In根据复合函数的性质S = S(N,U,β)S= S(N,U,V)S = S[N,U,β(U,V))asas) (%)asA+%) =((%)) +U1V.Aasd(m2)-1 (%)=-kβ+kauaβVN可以证明上式中的方括号等于零,故而得
, 值的推导 根据复合函数的性质 ln i S kN e k U = − S S N U = ( , , ) S S N U V = ( , , ) S S N U U V = [ , , ( , )] , , , V N N V N U N, S S S U U U = + ( ) , , , ln i V N V N U N S k k N e U U U = − + − 可以证明上式中的方括号等于零,故而得

值的推导α,βZeBe -kβUS = kN Inas=-kβauV,Nas因为7audU =TdS- pdV所以β=-kTe-e/krN.=N-e,/kTZ这就是Boltzmann最概然分布公式
, 值的推导 ln i S kN e k U = − V N, S k U = − 因为 d d d U T S p V = − , 1 V N S U T = 所以 1 kT = − / * / i i kT i kT e N N e − − = 这就是Boltzmann最概然分布公式