
山东理工大客SHANDONGUNIVERSITYOFTECHNOLOGY米$ 11.8关于活化能活化能概念的进一步说明理工活化能与温度的关系活化能的估算
1 *§11.8 关于活化能 活化能概念的进一步说明 活化能与温度的关系 活化能的估算

山东理工大客* S 11.8关于活化能SHANDONGUNIVERSITYOFTECHNOLOGY活化能概念的进一步说明概述在Arrhenius经验式中,把活化能看作是与温度无关的常数,这在一定的温度范围内与实验结果是相符的。如果实验温度范围适当放宽或对于较复杂的反应就不是一条很好的直线,这表明活化能与温度有关,而且Arrhenius经验式对某些历程复杂的反应不适用。对于基元反应,活化能有较明确的物理意义,而复杂反应的活化能仅是基元反应活化能的特定组合
2 在Arrhenius经验式中,把活化能看作是与温度无关 的常数,这在一定的温度范围内与实验结果是相符的。 对于基元反应,活化能有较明确的物理意义,而 复杂反应的活化能仅是基元反应活化能的特定组合。 如果实验温度范围适当放宽或对于较复杂的反应, 就不是一条很好的直线,这表明活化能与温度有关,而 且Arrhenius经验式对某些历程复杂的反应不适用。 活化能概念的进一步说明 *§11.8 关于活化能 概述

山东理工大客* $ 11.8关于活化能SHANDONGUNIVERSITYOFTECHNOLOGY活化能概念的进一步说明基元反应的活化能Tolman用统计平均的概念对基元反应的活化能下了一个定义:活化分子的平均能量与反应物分子平均能量之差值,称为活化能。E, =E -ER设基元反应为PA正、逆反应的活化能E.和E可以用图表示
3 Tolman 用统计平均的概念对基元反应的活化能下了一个 定义:活化分子的平均能量与反应物分子平均能量之差值, 称为活化能。 设基元反应为 A P 正、逆反应的活化能 Ea 和 ' 可以用图表示。 Ea * R E E E a = − *§11.8 关于活化能 活化能概念的进一步说明 基元反应的活化能
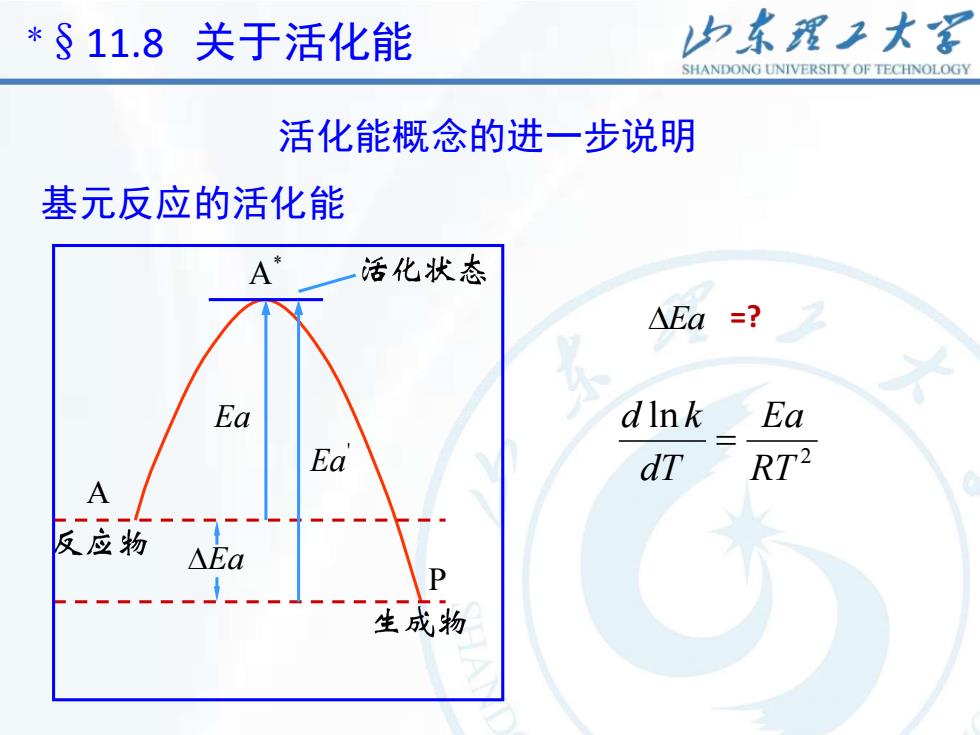
山东理工大客* $ 11.8关于活化能SHANDONGUNIVERSITYOFTECHNOLOGY活化能概念的进一步说明基元反应的活化能A*活化状态=?NEaEadlnkEaEaRT2dTA反应物AEaP生成物
4 EaEa ' Ea * A A P 基元反应的活化能 *§11.8 关于活化能 活化能概念的进一步说明 Ea =? 2 ln RT Ea dT d k =

山东理工大客* $ 11.8关于活化能SHANDONGUNIVERSITYOFTECHNOLOGY活化能概念的进一步说明基元反应的活化能假设有一基元反应(低压气相反应)k.理工A + BC+ DkEEdlnkd lnkd In(k / k_)a,+aRT2RT2dTdTdTr+= k,[A][B],r_= k_ [C][D]r+=r_时,反应达动态平衡,即k,[A]e[B]e=k_[C]e[D]
5 假设有一基元反应(低压气相反应) k+ k− A + B C + D 基元反应的活化能 活化能概念的进一步说明 *§11.8 关于活化能 dT d k dT d k+ − − ln ln − = + − 2 , 2 , RT E RT Ea a dT d ln(k / k ) + − = r+ = k+ [A][B], r−= k− [C][D] r + =r−时,反应达动态平衡,即 k+ [A]e [B]e=k− [C]e [D]e