
这个微分方程与式(8一1)相似,其通解为 R it(t)=Ke i (t≥0) 代入初始条件i(0)户I求得 K=Io 最后得到电感电流和电感电压的表达式为 R ,0=le7=l,e (t≥0) (8-7a)》 40=L-,e-u,e (t>0) (8-7b)
这个微分方程与式(8-1)相似,其通解为 ( ) e ( 0) L i t K t t L R 代入初始条件iL (0+ )=I 0求得 0 K I 最后得到电感电流和电感电压的表达式为 ( 0) (8 7b) d d ( ) ( ) e e ( 0) (8 7a) τ 0 0 L L τ L 0 0 R I e R I e t t i u t L i t I I t t t L R t t L R

其波形如图所示。RL电路零输入响应也是按指数规律 衰减,衰减的快慢取决于常数x。由于=LR具有时间的量 纲,称为RL电路的时间常数。 uL(t) iL(D) 0 T2r3π4r5Tt 0 2π3r4r5Tt -RIo (a) (b) 图8-7
其波形如图所示。RL电路零输入响应也是按指数规律 衰减,衰减的快慢取决于常数 。由于 =L/R具有时间的量 纲,称为RL电路的时间常数。 图8-7

例8-2电路如图8-8(a)所示,开关S,连接至1端已经很久, t=0时开关S由1端倒向2端。 求t≥0时的电感电流i() 和电感电压4()。 2 2002 i t=0 i 0.1A 202 4000 2002 0.2H34L 2002 0.2H2 (a) (b) 图8-8 解:开关转换瞬间,电感电流不能跃变,故 i(0+)=i(0_)=0.1A
例8-2 电路如图8-8(a)所示,开关S1连接至1端已经很久, t=0时开关S由1端倒向2端。求t0时的电感电流iL (t) 和电感电压uL (t)。 图8-8 解:开关转换瞬间,电感电流不能跃变,故 i L (0 ) i L (0 ) 0.1A
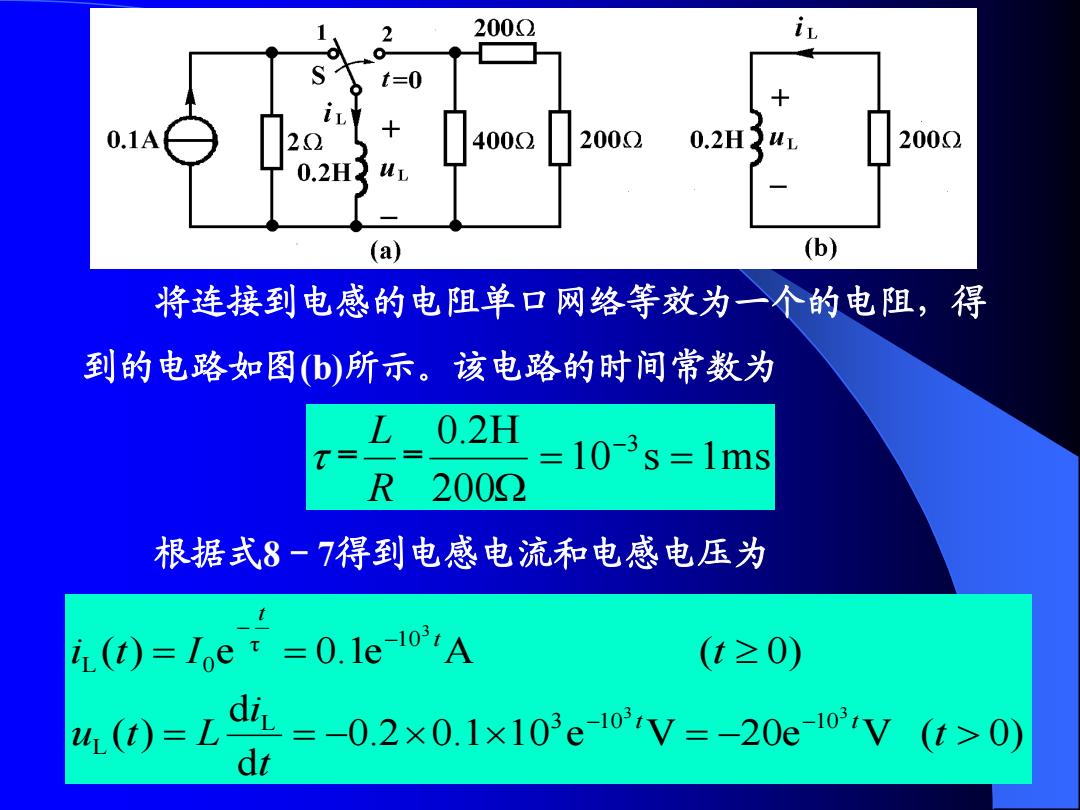
2 2002 i证 S t=0 0.1A 4000 2002 0.2H3 20002 0.2H2 (a) (b) 将连接到电感的电阻单口网络等效为一个的电阻,得 到的电路如图(b)所示。该电路的时间常数为 0.2H =10-3s=1ms R 2000 根据式8-7得到电感电流和电感电压为 it(t)=loe t=0.le-10A (t≥0)》 4,0=Ld此=-0.2x0.1x10eV=-20e0VG>0) dt
将连接到电感的电阻单口网络等效为一个的电阻,得 到的电路如图(b)所示。该电路的时间常数为 10 s 1ms 200 0.2H 3 = = R L 根据式8-7得到电感电流和电感电压为 0.2 0.1 10 e V 20e V ( 0) d d ( ) ( ) e 0.1e A ( 0) 3 3 3 L 3 10 10 L τ 10 L 0 t t i u t L i t I t t t t t

通过对RC和RL一阶电路零输入响应的分析和计算表 明,电路中各电压电流均从其初始值开始,按照指数规律 衰减到零,一般表达式为 f)=f(.)e 因为电容或电感在非零初始状态时具有初始储能,各 元件有初始电压电流存在,由于电阻要消耗能量,一直要 将储能元件的储能消耗完,各电压电流均变为零为止
通过对RC和RL一阶电路零输入响应的分析和计算表 明,电路中各电压电流均从其初始值开始,按照指数规律 衰减到零,一般表达式为 t f (t) f (0 )e 因为电容或电感在非零初始状态时具有初始储能,各 元件有初始电压电流存在,由于电阻要消耗能量,一直要 将储能元件的储能消耗完,各电压电流均变为零为止