
§8-2零状态响应 初始状态为零,仅仅由独立电源(称为激励或输入)引 起的响应,称为零状态响应。本节只讨论由直流电源引起 的零状态响应。 一、RC电路的零状态响应 图8-9(a)所示电路中的电容原来未充电,uc(0)=0。-0 时开关闭合,RC串联电路与直流电压源连接,电压源通过 电阻对电容充电
§8-2 零状态响应 初始状态为零,仅仅由独立电源(称为激励或输入)引 起的响应,称为零状态响应。本节只讨论由直流电源引起 的零状态响应。 一、 RC电路的零状态响应 图8-9(a)所示电路中的电容原来未充电,uC (0- )=0。t=0 时开关闭合,RC串联电路与直流电压源连接,电压源通过 电阻对电容充电
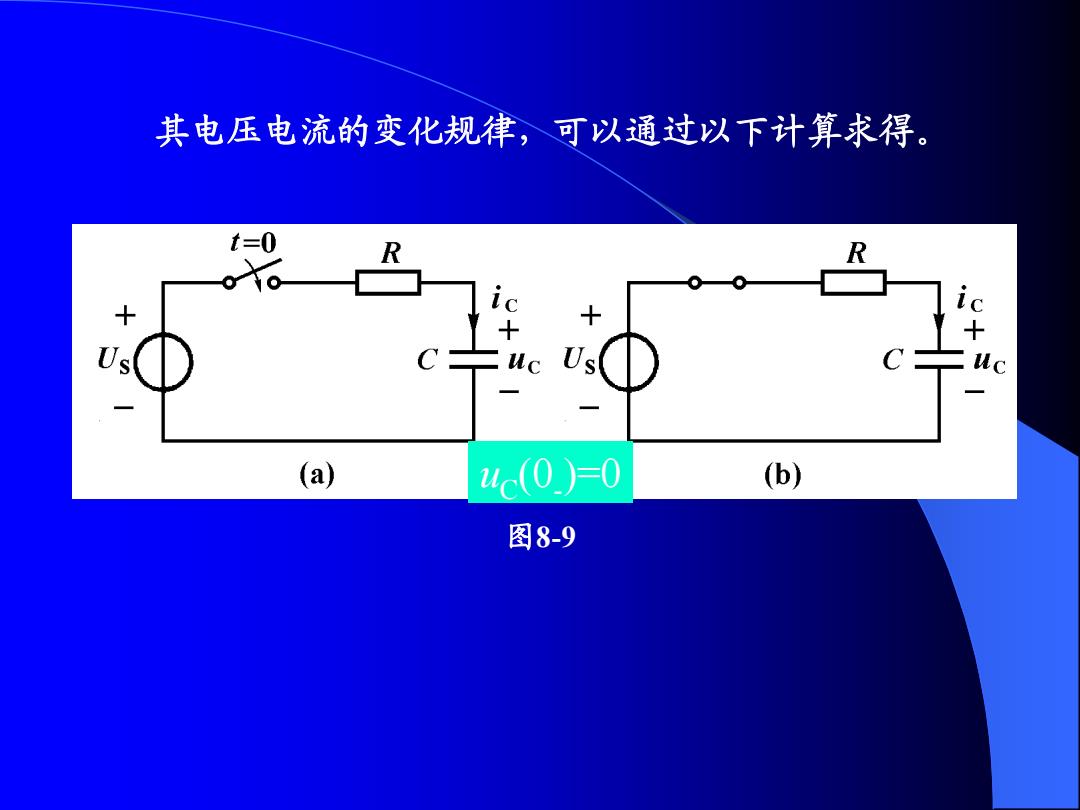
其电压电流的变化规律,可以通过以下计算求得。 t=0 R R ic ic uc (a) 4c(0)=0 (b) 图8-9
图8-9 uC (0- )=0 其电压电流的变化规律,可以通过以下计算求得
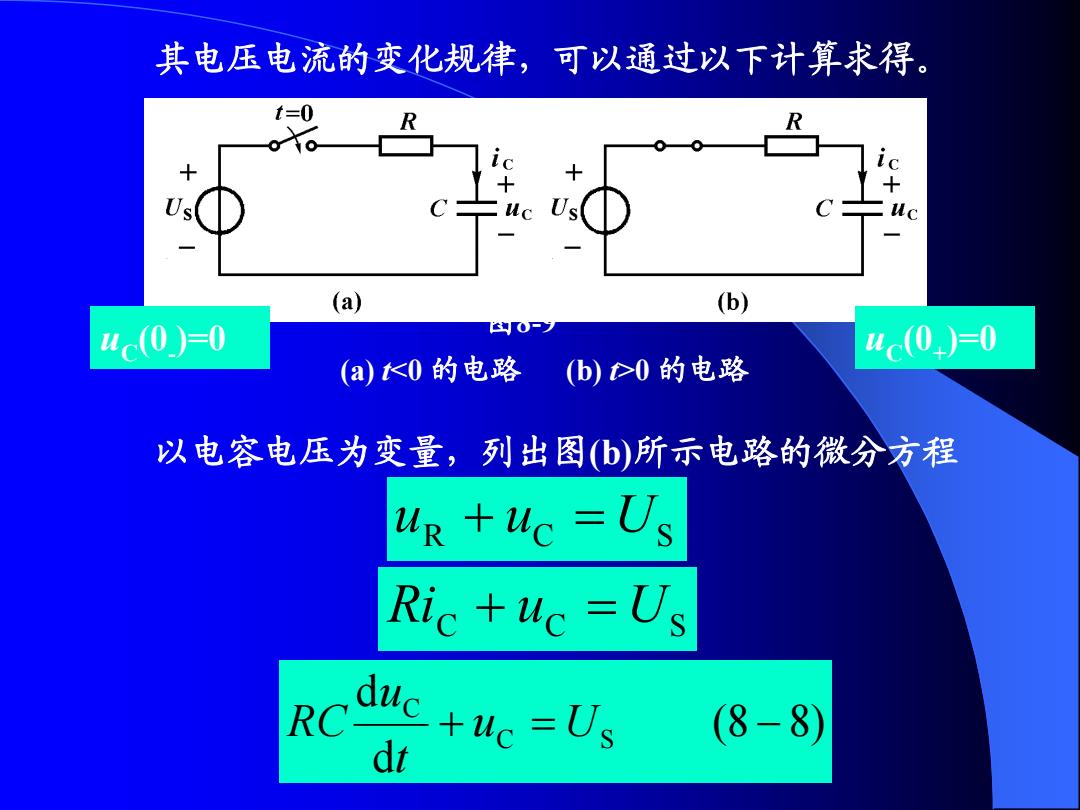
其电压电流的变化规律,可以通过以下计算求得 (a) (b) uc(0=0 uc(0)=0 (a)0的电路 (b)>0的电路 以电容电压为变量,列出图(b)所示电路的微分方程 ur +uc =Us Ric +uc =Us duc+uc =Us RC (8-8) dr
(a) t<0 的电路 (b) t>0 的电路 以电容电压为变量,列出图(b)所示电路的微分方程 uR uC US C C US Ri u (8 8) d d C S C u U t u R C 图8-9 uC (0- )=0 uC (0+ )=0 其电压电流的变化规律,可以通过以下计算求得

RC duc+uc=Us (8-8) dt 这是一个常系数线性非齐次一阶微分方程。其解答由 两部分组成,即 uc(t)=uch (1)+ucp (t) (8-9)》 式中的4c()是与式(8-8)相应的齐次微分方程的通 解,其形式与零输入响应相同,即 uch (t)=Kes =Ke RC (t20)
这是一个常系数线性非齐次一阶微分方程。其解答由 两部分组成,即 ( ) ( ) ( ) (8 9) uC t uCh t uCp t 式中的uCh(t)是与式(8-8)相应的齐次微分方程的通 解,其形式与零输入响应相同,即 ( ) e e ( 0) Ch u t K K t RC t st (8 8) d d C S C u U t u R C

式(8-)中的4cp)是式(8-8)所示非齐次微分方程的 一个特解。一般来说,它的模式与输入函数相同。对于直 流电源激励的电路,它是一个常数,令 4c,())=Q RCde+ue=U、 (8-8)》 dr 将它代入式(8-8)中求得 4c,()=O=Us 因而 uc(t)=uch (1)+ucp (t)=Ke Rc+Us (8-10)
式(8-9)中的uCp(t)是式(8-8)所示非齐次微分方程的 一个特解。一般来说,它的模式与输入函数相同。对于直 流电源激励的电路,它是一个常数,令 uCp (t) Q 将它代入式(8-8)中求得 Cp S u (t) Q U 因而 ( ) ( ) ( ) e (8 10) C Ch Cp S u t u t u t K RC U t (8 8) d d C S C u U t u R C