6k2 8k2 t=0 3k2 +10k2 5μF三 uc 5μF ic ic (a) (b) 将连接于电容两端的电阻单口网络等效于一个电阻, 其电阻值为 6×3 R。=(8+ 6+ k2=10k2 得到图(b)所示电路,其时间常数为 =2×J0s2=0^022 10k2 5μF 上=5C=J0×J03×2×J0.2 ic (b)
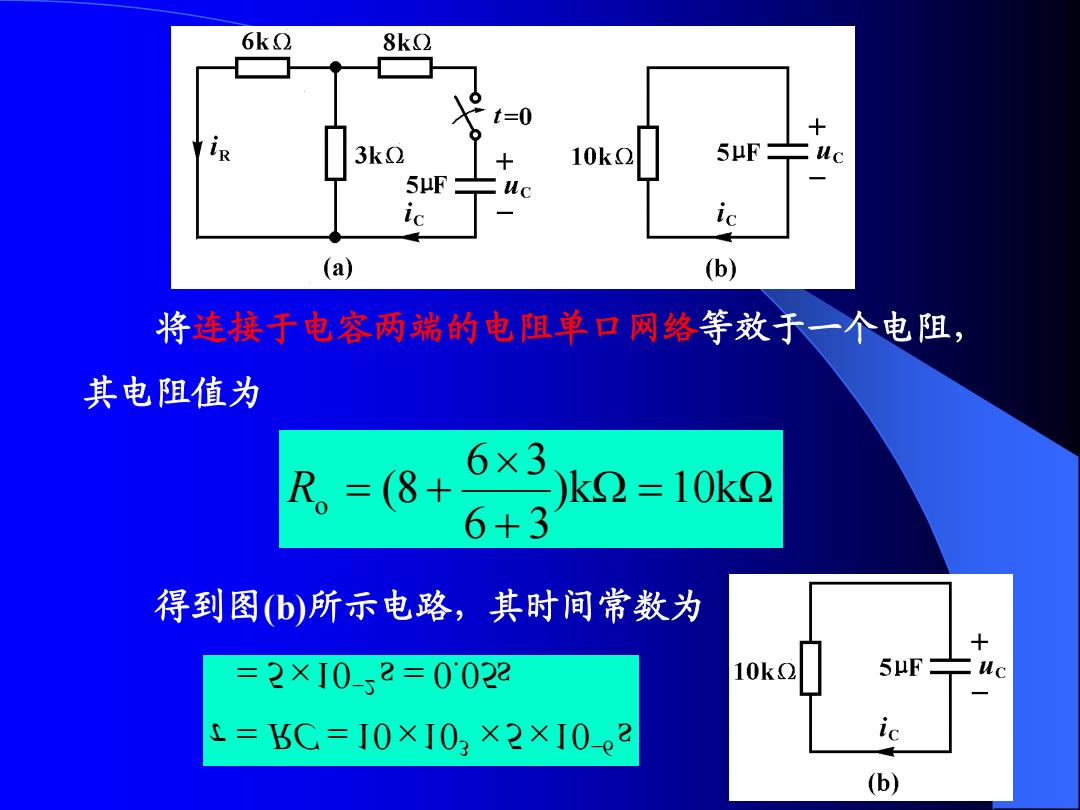
将连接于电容两端的电阻单口网络等效于一个电阻, 其电阻值为 )k 10k 6 3 6 3 Ro (8 得到图(b)所示电路,其时间常数为 5 10 s 0.05s 10 10 5 10 s 2 3 6 RC

根据式8-5得到 uc(t)=Ue r=6e-20V (t≥0) 6k2 8k2 e0=cdwe=-么e t=0 dt R 3k2 6 5μF Wc e-20 mA ic 10×10 =-0.6e-20mA (t>0) (a) 电阻中的电流()可以用与i()同样数值的电流源代替 电容,用电阻并联的分流公式求得() 0=3640=06enA-02omA 3 3
根据式8-5得到 0.6e m A ( 0) e m A 10 10 6 e d d ( ) ( ) e 6e V ( 0) 20 20 3 C 0 C 20 C 0 t R U t u i t C u t U t t t t t t 电阻中的电流iR (t)可以用与iC (t)同样数值的电流源代替 电容,用电阻并联的分流公式求得 iR (t) 0.6e mA 0.2e mA 3 1 ( ) 3 6 3 ( ) 20 20 R C t t i t i t

二、RL电路的零输入响应 我们以图8-6(a电路为例来说明RL电路零输入响应的 计算过程。 0 (a) (b) 图8-6 电感电流原来等于电流1,电感中储存一定的磁场能 量,在=0时开关由1端倒向2端,换路后的电路如图(b)所 示
二、RL电路的零输入响应 电感电流原来等于电流I 0,电感中储存一定的磁场能 量,在t=0时开关由1端倒向2端,换路后的电路如图(b)所 示。 图8-6 我们以图8-6(a)电路为例来说明RL电路零输入响应的 计算过程

在开关转换瞬间,由于电感电流不能跃变,即0+)尸 0)=1,,这个电感电流通过电阻R时引起能量的消耗, 这就造成电感电流的不断减少,直到电流变为零为止。 综上所述,图(b)所示RL电 iv 路是电感中的初始储能逐渐释 十 十 放出来消耗在电阻中的过程。 R W 与能量变化过程相应的是各电 压电流从初始值,逐渐减小到 零的过程。 (b)
在开关转换瞬间,由于电感电流不能跃变,即iL (0+ )= iL (0- )= I 0 ,这个电感电流通过电阻R时引起能量的消耗, 这就造成电感电流的不断减少,直到电流变为零为止。 综上所述,图(b)所示RL电 路是电感中的初始储能逐渐释 放出来消耗在电阻中的过程。 与能量变化过程相应的是各电 压电流从初始值,逐渐减小到 零的过程
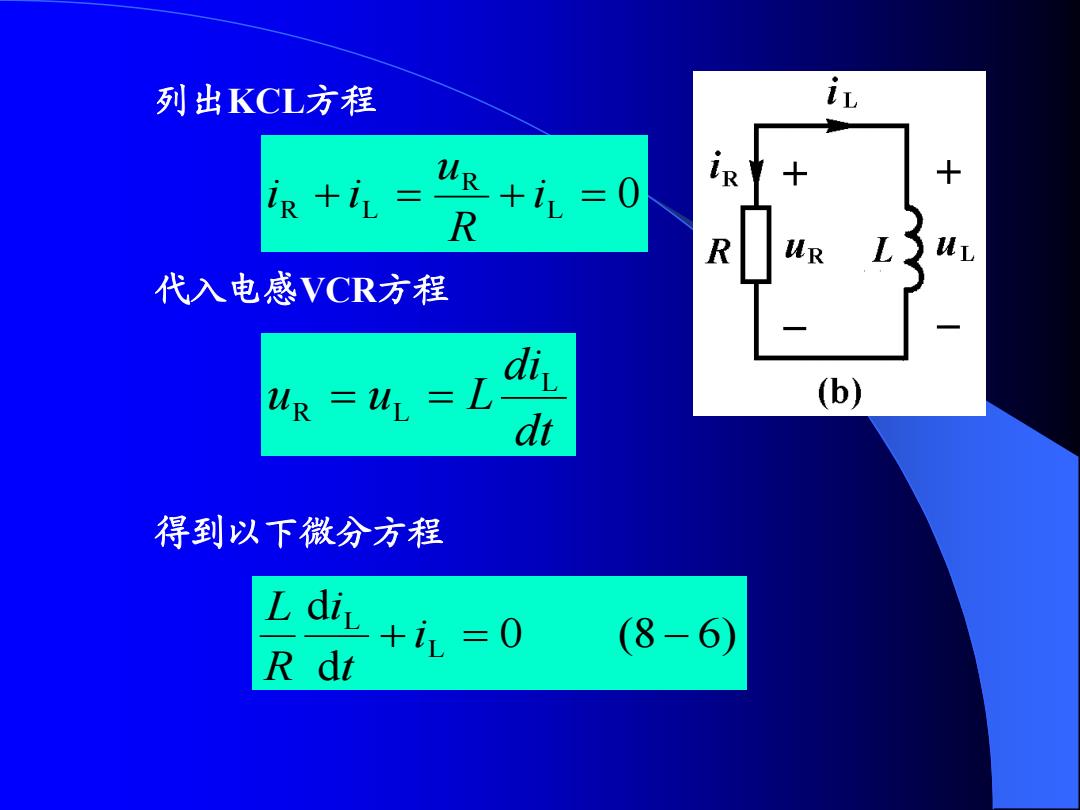
列出KCL方程 i取+i= +i=0 R R us 代入电感VCR方程 uR =u =L di (b) dt 得到以下微分方程 +i=0 (8-6) R dt
列出KCL方程 L 0 R R L i R u i i 代入电感VCR方程 dt di u u L L R L 得到以下微分方程 0 (8 6) d d L L i t i R L