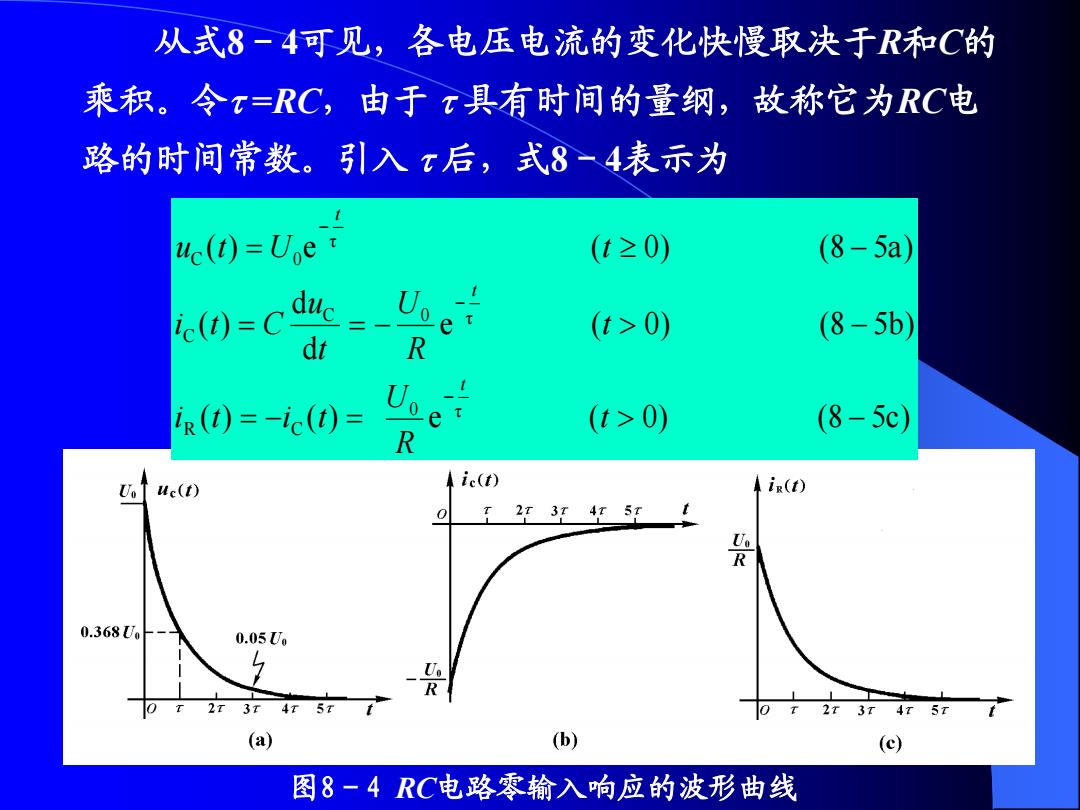
从式8一4可见,各电压电流的变化快慢取决于R和C的 乘积。令x=RC,由于具有时间的量纲,故称它为RC电 路的时间常数。引入x后,式8-4表示为 uc(t)=Uoe (t≥0) (8-5a) 0)= dlc三一 R (t>0) (8-5b) i()=-c()= e (t>0) (8-5c) R Uo ue(t) ic(t) iR(t) 0 234红5 发 0.368Uo- 0.05Uo 0 2T 3T 4T 5T 0 T (a) (b) (c) 图8-4RC电路零输入响应的波形曲线
从式8-4可见,各电压电流的变化快慢取决于R和C的 乘积。令 =RC,由于 具有时间的量纲,故称它为RC电 路的时间常数。引入 后,式8-4表示为 图8-4 RC电路零输入响应的波形曲线 ( ) ( ) e ( 0) (8 5c) e ( 0) (8 5b) d d ( ) ( ) e ( 0) (8 5a) 0 τ R C C 0 τ C τ C 0 t R U i t i t t R U t u i t C u t U t t t t

下面以电容电压 4e()=U,e为例,说明电压的变化与 时间常数的关系。 当0时,4c(0=Uo,当=时,uc(=0.368U。表8-1 列出等于0,,2x,3x,4x,5x时的电容电压值,由于波 形衰减很快,实际上只要经过4~5的时间就可以认为放电 过程基本结束。 0 T 2t 3t 4t 5t 00 4.() 0.368U0 0.135U0 0.050U0 0.018U0 0.007U 0
下面以电容电压 为例,说明电压的变化与 时间常数的关系。 τ C 0 ( ) e t u t U 当t=0时,uC (0)=U0,当t=时,uC ()=0.368U0。表8-1 列出t等于0,,2,3,4,5 时的电容电压值,由于波 形衰减很快,实际上只要经过4~5的时间就可以认为放电 过程基本结束。 t 0 2 3 4 5 uc (t) U0 0.368U0 0.135U0 0.050U0 0.018U0 0.007U0 0

uc(t) ◆ic(t) in(t) 2红3江 AT 5T 鉴 0.368U 0.05Uo 2T 3T 4T 5T (a) (b) (c) 图8-4RC电路零输入响应的波形曲线 电阻在电容放电过程中消耗的全部能量为 Wa=nR0R=%e忘yRar-cUg R 2 计算结果证明了电容在放电过程中释放的能量的确金 部转换为电阻消耗的能量
电阻在电容放电过程中消耗的全部能量为 0 0 2 0 2 0 2 R R 2 1 ( ) d ( e ) Rdt CU R U W i t R t R C t = 计算结果证明了电容在放电过程中释放的能量的确全 部转换为电阻消耗的能量。 图8-4 RC电路零输入响应的波形曲线

由于电容在放电过程中释放的能量全部转换为电阻消 耗的能量。电阻消耗能量的速率直接影响电容电压衰减的 快慢,我们可以从能量消耗的角度来说明放电过程的快慢, 例如在电容电压初始值心不变的条件下,增加电容C, 就增加电容的初始储能,使放电过程的时间加长;若增加 电阻R,电阻电流减小,电阻消耗能量减少,使放电过程 的时间加长。 这就可以解释当时间常数后RC变大,电容放电过程会 加长的原因
由于电容在放电过程中释放的能量全部转换为电阻消 耗的能量。电阻消耗能量的速率直接影响电容电压衰减的 快慢,我们可以从能量消耗的角度来说明放电过程的快慢。 例如在电容电压初始值U0不变的条件下,增加电容C, 就增加电容的初始储能,使放电过程的时间加长;若增加 电阻R,电阻电流减小,电阻消耗能量减少,使放电过程 的时间加长。 这就可以解释当时间常数=RC变大,电容放电过程会 加长的原因
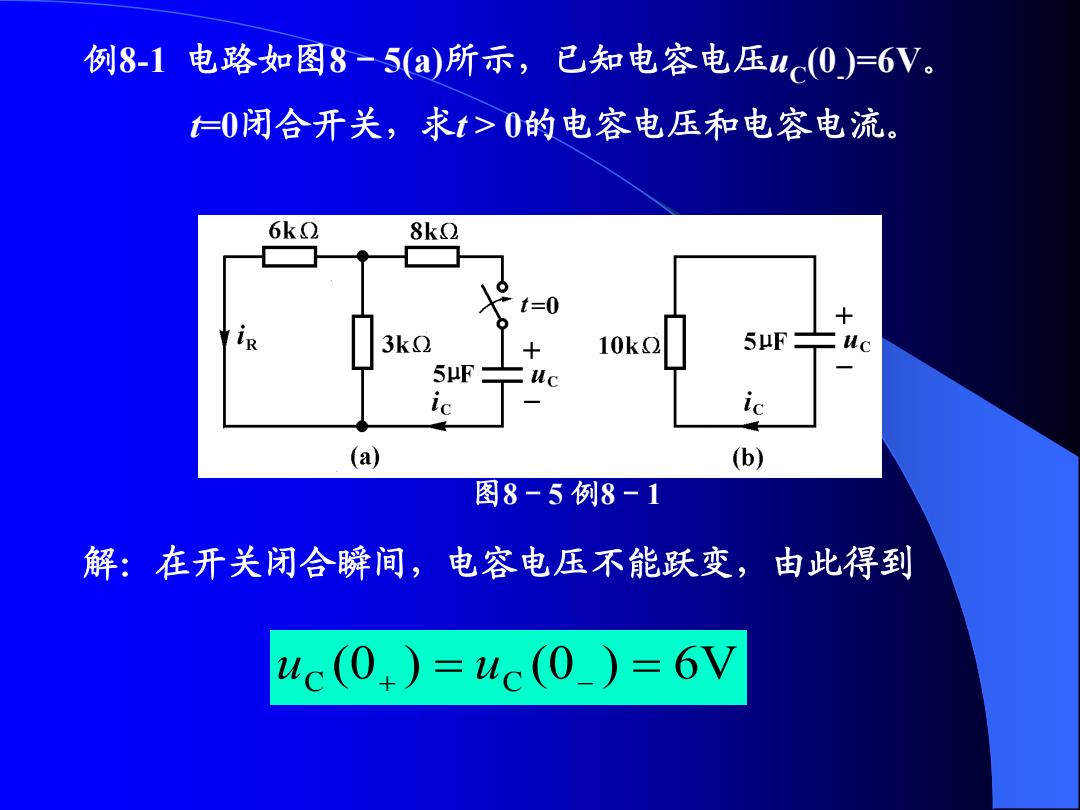
例8-1电路如图8-5(a所示,已知电容电压uc(0)=6V t仁0闭合开关,求t>0的电容电压和电容电流。 6k2 8k2 3k2 10k0 5μF 5μF ic ic (a) (b) 图8-5例8-1 解:在开关闭合瞬间,电容电压不能跃变,由此得到 uc(0+)=uc(0_)=6V
例8-1 电路如图8-5(a)所示,已知电容电压uC (0- )=6V。 t=0闭合开关,求t > 0的电容电压和电容电流。 图8-5 例8-1 解:在开关闭合瞬间,电容电压不能跃变,由此得到 uC (0 ) uC (0 ) 6V