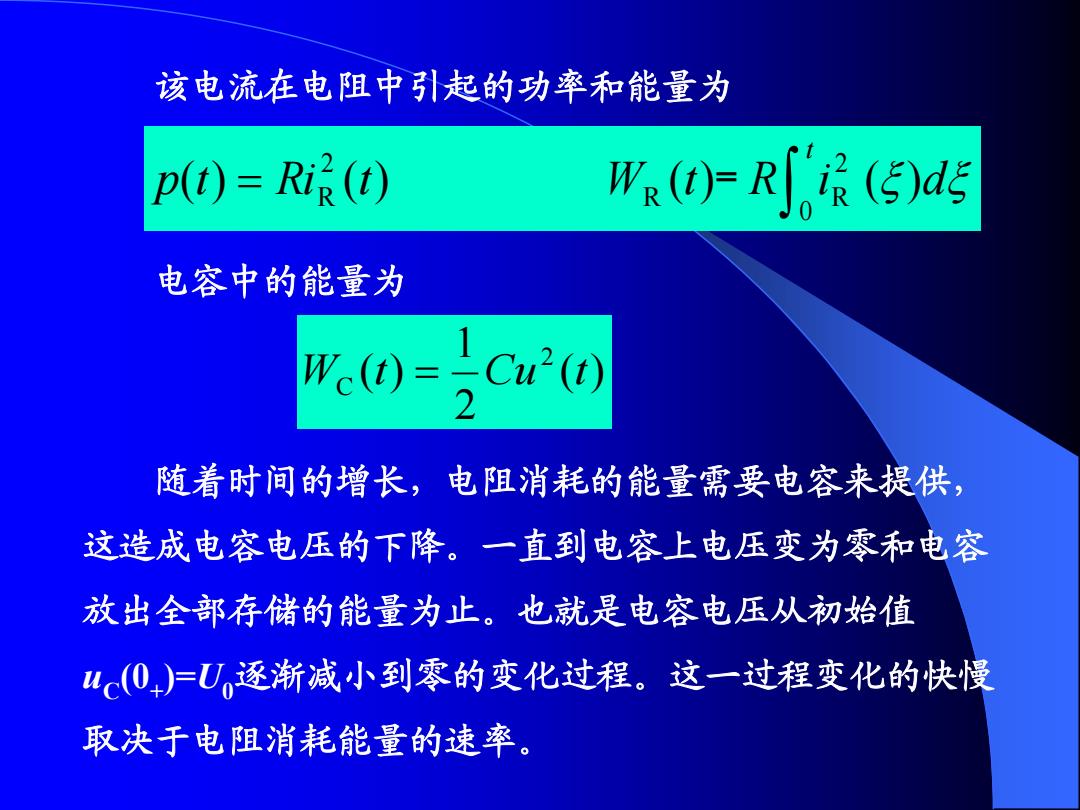
该电流在电阻中引起的功率和能量为 p0)=R() W()-R长(⑤d5 电容中的能量为 .0=a 随着时间的增长,电阻消耗的能量需要电容来提供, 这造成电容电压的下降。一直到电容上电压变为零和电容 放出全部存储的能量为止。也就是电容电压从初始值 “c0+)=U,逐渐减小到零的变化过程。这一过程变化的快慢 取决于电阻消耗能量的速率
该电流在电阻中引起的功率和能量为 t p t Ri t W t R i d 0 2 R R 2 R ( ) ( ) ( )= ( ) 电容中的能量为 ( ) 2 1 ( ) 2 C W t Cu t 随着时间的增长,电阻消耗的能量需要电容来提供, 这造成电容电压的下降。一直到电容上电压变为零和电容 放出全部存储的能量为止。也就是电容电压从初始值 uC (0+ )=U0逐渐减小到零的变化过程。这一过程变化的快慢 取决于电阻消耗能量的速率
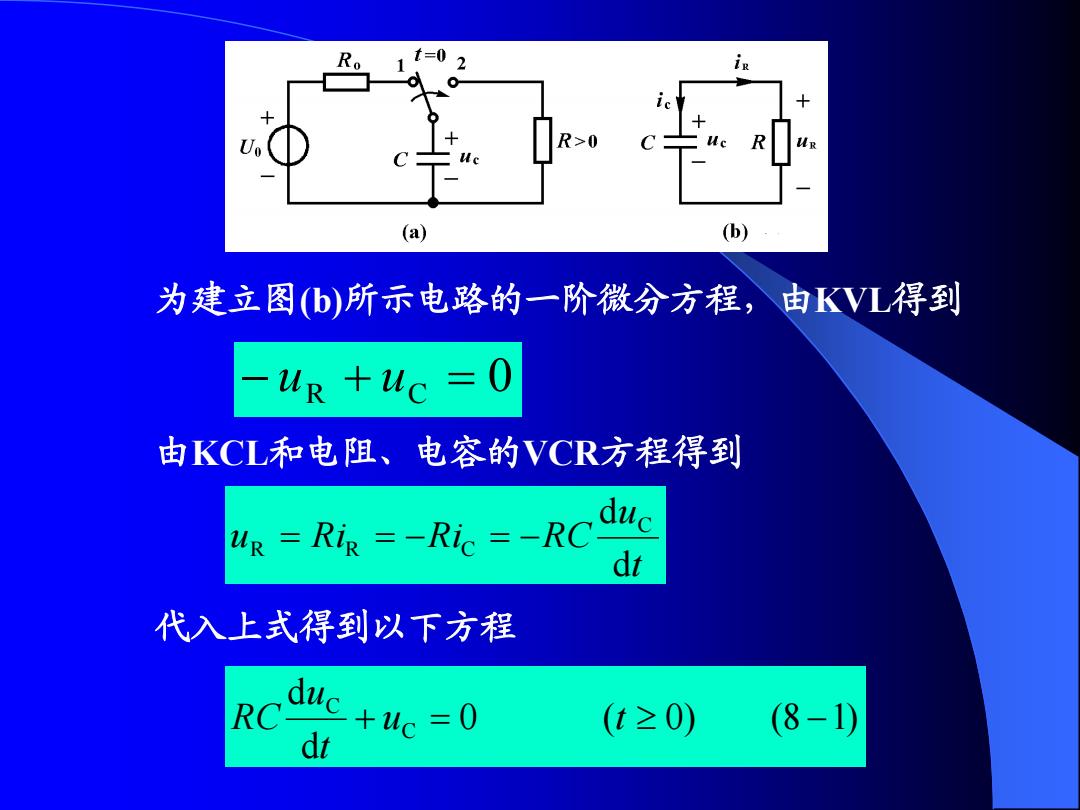
in C (a) (b) 为建立图(b)所示电路的一阶微分方程,由KVL得到 uR +uc =0 由KCL和电阻、电容的VCR方程得到 uR RiR =-Ric =-RC dt 代入上式得到以下方程 c+uc=0 RC- (t≥0) (8-1)》
为建立图(b)所示电路的一阶微分方程,由KVL得到 uR uC 0 由KCL和电阻、电容的VCR方程得到 t u u R i R i R C d d C R R C 代入上式得到以下方程 0 ( 0) (8 1) d d C C u t t u R C
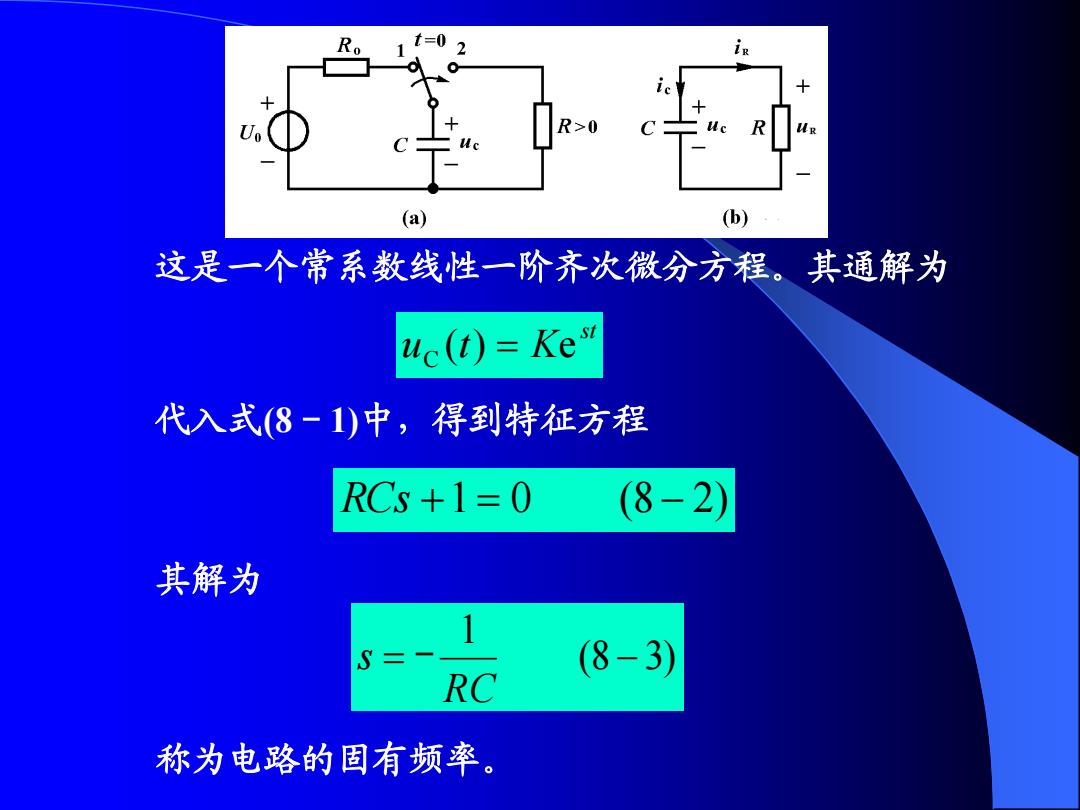
i (a) (b) 这是一个常系数线性一阶齐次微分方程。其通解为 uc(t)=Kes 代入式(8-1)中,得到特征方程 RCs+1=0 (8-2) 其解为 S (8-3) RC 称为电路的固有频率
这是一个常系数线性一阶齐次微分方程。其通解为 st u (t) Ke C 代入式(8-1)中,得到特征方程 RCs 1 0 (8 2) 其解为 (8 3) 1 R C s - 称为电路的固有频率
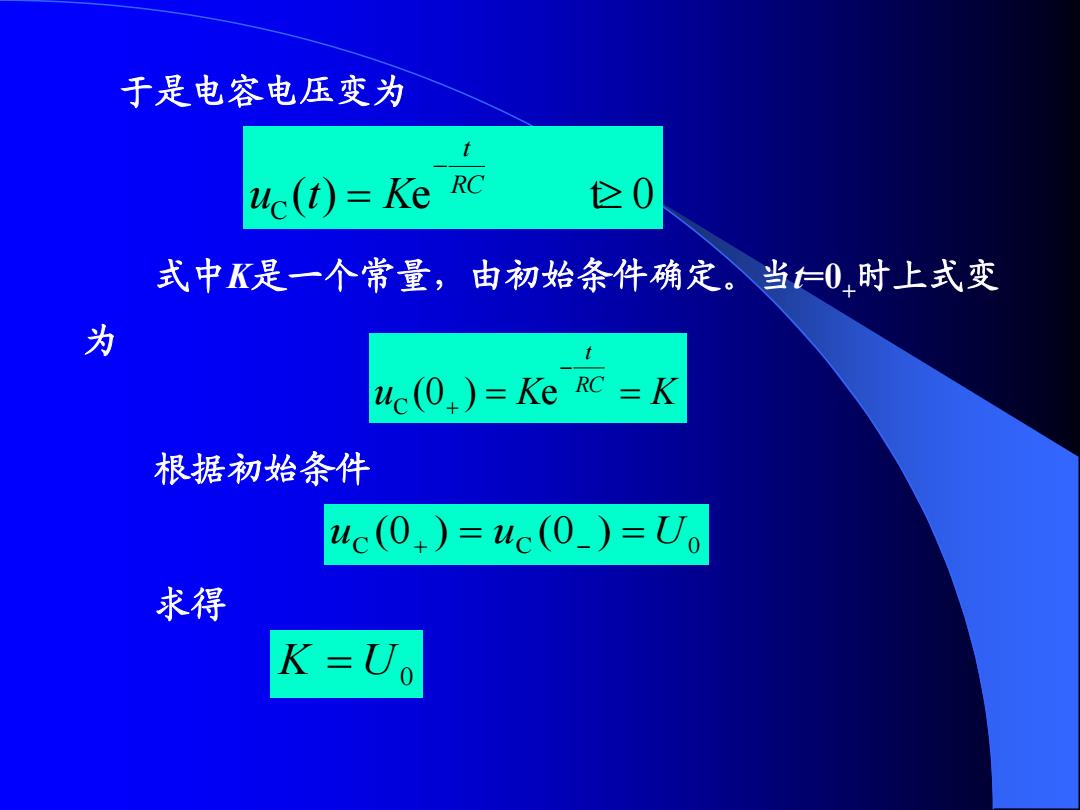
于是电容电压变为 uc(t)=Ke RC 0 式中K是一个常量,由初始条件确定。当仁0时上式变 为 uc(0.)=Ke RC =K 根据初始条件 uc(0+)=uc(0_)=Uo 求得 K=Uo
于是电容电压变为 C ( ) e t 0 RC t u t K 式中K是一个常量,由初始条件确定。当t=0+时上式变 为 u K RC K t (0 ) e C 根据初始条件 C C 0 u (0 ) u (0 ) U 求得 K U0
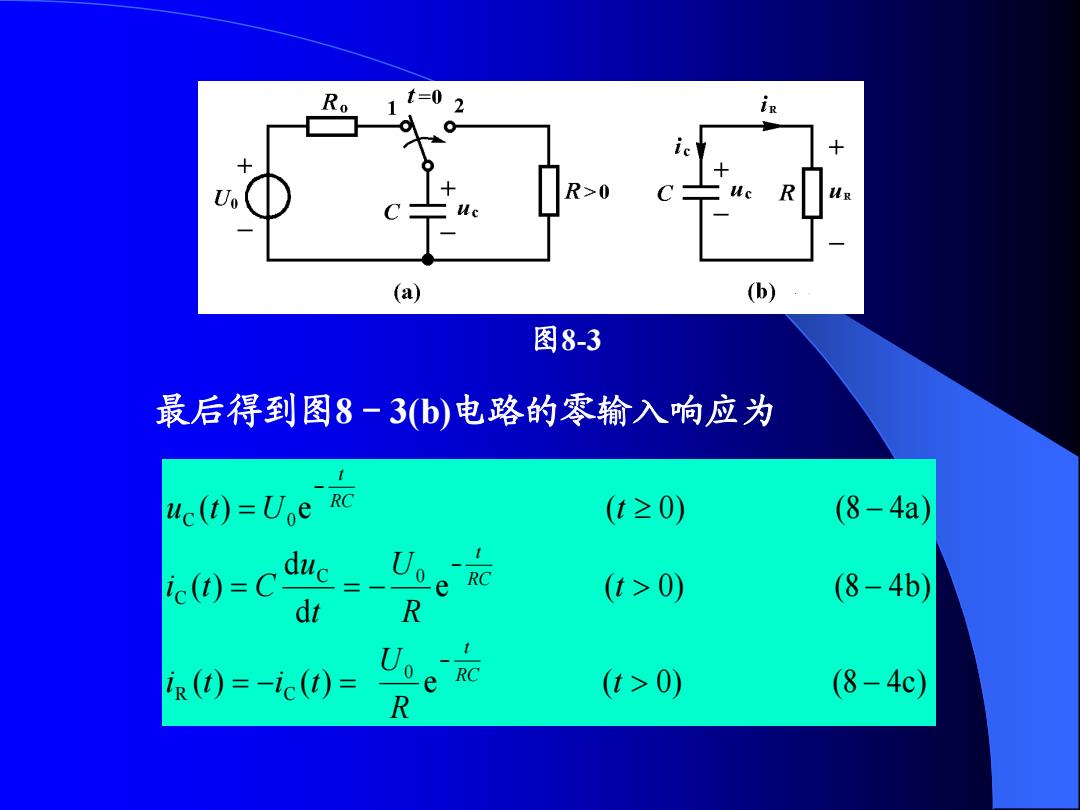
in (a) (b) 图8-3 最后得到图8-3b)电路的零输入响应为 4.()=Ued (t≥0)》 (8-4a) (t>0) (8-4b) dr R R(0=-ic()= U RC (t>0) (8-4c) R
( ) ( ) e ( 0) (8 4c) e ( 0) (8 4b) d d ( ) ( ) e ( 0) (8 4a) 0 R C C 0 C C 0 t R U i t i t t R U t u i t C u t U t R C t R C t R C t 最后得到图8-3(b)电路的零输入响应为 图8-3