
非线性物理:混沌物理 0<1:迭代单调的趋近x*,m>1表示迭代指数增长发散。 -1<0:迭代经过几次上下起伏趋近于x*,<-1表示迭代指数 振荡增长发散。 周期解: 按照上述稳定性分析,从初值x出发,迭代过程要么发散,要么 收敛到两个定常态之一。然而,在合适的μ值情况下,迭代过程 表现为:xf小,xf,循环往复,出现倍周期解。 周期2解应该满足:x=ffx)》→f2x),周期4解满足 x=f0f0f0f》→f4)
非线性物理:混沌物理 • 0<m<1:迭代单调的趋近 x*,m>1表示迭代指数增长发散。 • -1<m<0:迭代经过几次上下起伏趋近于 x*, m<-1表示迭代指数 振荡增长发散。 • 周期解: • 按照上述稳定性分析,从初值 x0 出发,迭代过程要么发散,要么 收敛到两个定常态之一。然而,在合适的 值情况下,迭代过程 表现为:x2=f(x1),x1=f(x2),循环往复,出现倍周期解。 • 周期2解应该满足:x=f(f(x)) f 2(x),周期4解满足 x=f(f(f(f(x)))) f 4(x)

非线性物理:混沌物理 以x=f2x为例,方程变为: x=f(f(x》=4I(1-x][1-(1-x)] x-4[x(1-x][1-x(1-x]=O ·方程x=fx的两个定常解依然是上述方程的两个根,从而求得另 外两个根: -〔--++u--0 ,=(+1)生u+1u-3 24
非线性物理:混沌物理 • 以 x=f 2 (x)为例,方程变为: • 方程 x=f (x)的两个定常解依然是上述方程的两个根,从而求得另 外两个根:

非线性物理:混沌物理 实根x2要求4>3,也就是说,只要满足此条件,周期2解一定存 在。如μ=3.2,有x=0.513,x2=0.799。 ·周期4、周期8、及至周期2"的根可以依此类推求解出来,剔除掉 低倍周期的全部根,剩余的实根数目就是2“,对应于周期2解。 ·在μ=3.57时,n趋向无穷,即混沌解! 0.8 0.6 V 08 0.4 μ=3.1 型 0.4 0.2 =3.S2 0.2 6 0.0 10 15202530
非线性物理:混沌物理 • 实根 x1,2要求 >3,也就是说,只要满足此条件,周期2解一定存 在。如 =3.2,有 x1=0.513,x2=0.799。 • 周期4、周期8、及至周期 2n 的根可以依此类推求解出来,剔除掉 低倍周期的全部根,剩余的实根数目就是2n,对应于周期2n解。 • 在 =3.57时,n趋向无穷,即混沌解!
非线性物理:混沌物理 倍周期的图形解: Xn+l =3.3 0.8 0.6 0.4 再演示一下倍周期分叉过程。 0.2 0 Xn+2 0.8 1/2 d3 0.6 0.4 0.2 4R M:RR 00.20.40.60.81 福 Xn
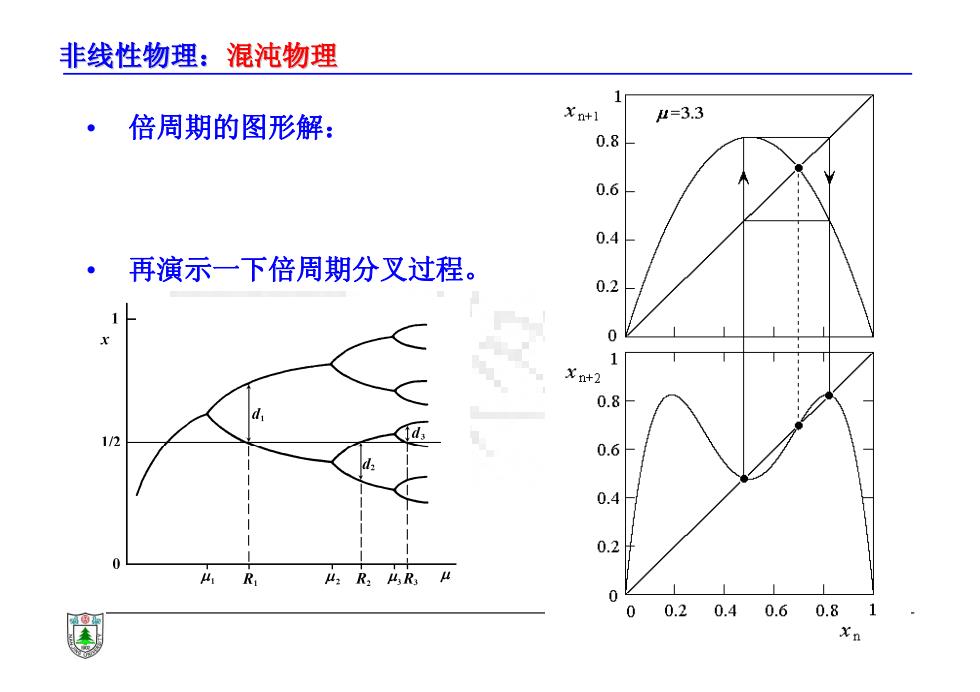
非线性物理:混沌物理 • 倍周期的图形解: • 再演示一下倍周期分叉过程

非线性物理:混沌物理 驱动与耗散的竞争: ·从物理本质上看,分岔是非线性系统驱动力和耗散力竞争达到临 界状态而对应的演化行为转变。再以平方映射为例: Xn1=Ln (1-xn) 显然,心n是驱动力,心是耗散力,两者之间竞争导致状态的 丰富多样。在定常态附近判断两力相对大小依赖于: 6xn+1 of x=x*
非线性物理:混沌物理 驱动与耗散的竞争: • 从物理本质上看,分岔是非线性系统驱动力和耗散力竞争达到临 界状态而对应的演化行为转变。再以平方映射为例: (1 ) n 1 n n x x x • 显然,xn是驱动力,-xn2是耗散力,两者之间竞争导致状态的 丰富多样。在定常态附近判断两力相对大小依赖于: