
>余项Rnx)的确定 R(x)=f(x)-P(x) R(x)=p(x)-f(x)=0(k=0,1,2,m) lim R,(x) lim R'(x) R(x)=R(x)=0 x->xo ()"n) R"(x) lim 使用洛必 R(x)=0 m(n-10(x-x,))- 法则 =.lim ) x→n(x-x) R%-(x)=0 1 =lim -R-()=1 n!x-→x x-xo ()=0
➢ 余项R n (x )的确定 ( ) ( ) ( ) 0 ( ) 0 ( ) 0 ( ) R x p x f x k k n k n = − = 0 ( k = 0 , 1 , 2 , , n ) 0 0 ( ) lim ( ) n n x x R x → x x − 0 1 0 ( ) lim ( ) n n x x R x n x x → − = − 0 2 0 ( ) lim ( 1)( ) n n x x R x n n x x → − = − − = 多次使用洛必达法则 0 ( 1) 0 ( ) lim !( ) nn x x R x n x x − → = − 0 0 ( ) ( ) 0 R x R x n n = = 0 ( ) 0 R x n = ( 1) 0 ( ) 0 n R x n − = 0 ( 1) ( 1) 0 0 1 ( ) ( ) lim ! n n n n x x R x R x n x x − − → − = − ( ) 0 1 ( ) ! n R x n n = = 0

> 泰勒(Taylor)中值定理1 如果函数f(x)在x,处具有阶导数,那么存在x,的一个邻域, 对于该邻域内的任一x,有 函数fx)按c-xo)的幂展开的 动多项司 +( 带有佩亚诺余项的阶泰勒公式 其中 R.(x)
➢ 泰勒(Taylor)中值定理1 如果函数 在 处具有n阶导数,那么存在 对于该邻域内的任一x,有 其中 函数f (x)按(x-x0 )的幂展开的n次泰勒多项式 佩亚诺 余项 函数f (x)按(x-x0 )的幂展开的 带有佩亚诺余项的n阶泰勒公式 的一个邻域
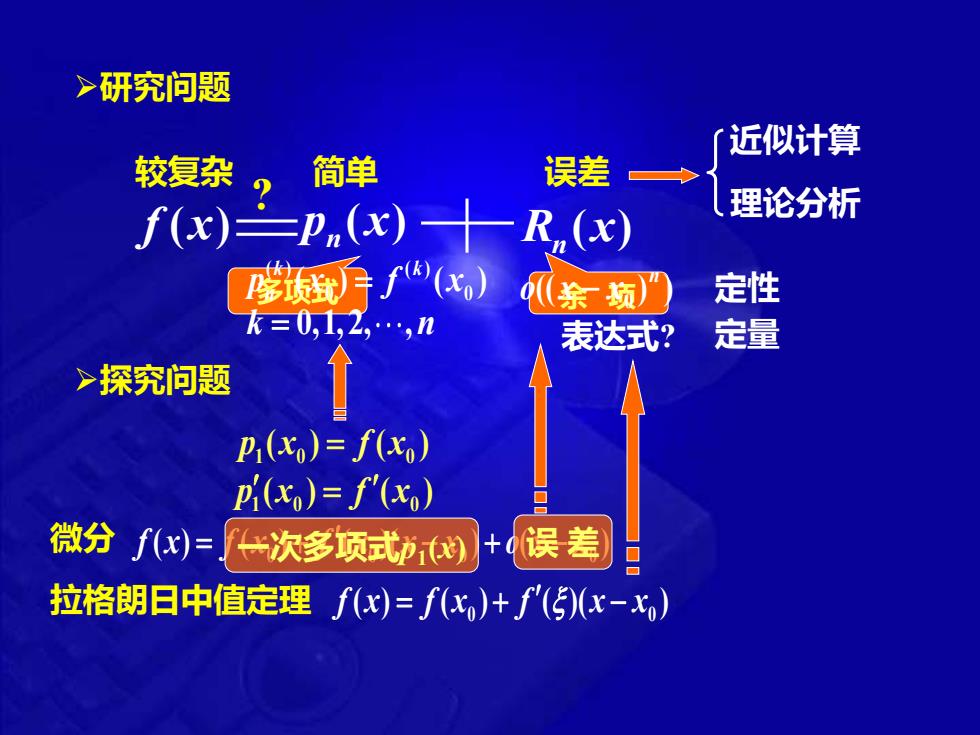
>研究问题 近似计算 较复杂 简单 误差 f(x)=P,(x) 理论分析 R,(x) 学逅手f(x) 案频门 定性 k三01,2Z,.,n 表达式? 定量 >探究问题 Pi(x)=f(xo) P(x)=f'(x) 微分∫x)=一次多顶式的+误差) 拉格朗日中值定理f(x)=f(化,)+∫'()(x-x,)
➢研究问题 f (x) 多项式 余 项 p (x) n R (x) n 较复杂 简单 误差 近似计算 理论分析 微分 ( ) ( ) ( )( ) ( ) 0 0 0 0 f x = f x + f x x − x + o x − x ( ) ( ) 1 0 0 p x = f x ( ) ( ) 1 0 0 p x = f x ( ) ( ) 0 ( ) 0 ( ) p x f x k k n = k n = 0,1,2, , (( ) ) 0 n o x − x 定性 定量 拉格朗日中值定理 ( ) ( ) ( )( ) 0 0 f x = f x + f x − x 表达式? ? 一次多项式p1 (x) 误 差 ➢探究问题

>余项R)的确定 R.(x)=f(x)-p.(x Rg(x。)=p(x)-f(x)=0(k=0,1,2,.,m) R(x)、 R(x)-R(Xo)_ R(5) (c-x)+1 (x-x)*1_0 (n+1)(5-x” (5在x,与x之间) 次使用 R(5)-R(xo) R(5) (n+10(51-x)0(n+1)n(52-x)-1 (5在x与51之间) 中值定理 R(5n)-R)-R*(5) fa*》(5) (n+1).2(5m-x)-0 (n+1)! (n+1)! (5在x与x之间)
➢ 余项Rn (x)的确定 ( ) ( ) ( ) 0 ( ) 0 ( ) 0 ( ) R x p x f x k k n k n = − = 0 (k = 0,1,2, ,n) 1 0 ( ) ( ) + − n n x x R x ( ) ( ) 1 0 + − = n n x x R x ( 1) 2( ) ( ) 0 ( ) n x R n n n n + − = n n n x R ( 1)( ) ( ) 1 0 1 + − = ( 1)( ) ( ) 1 0 1 n n n x R + − = 1 2 0 2 ( 1) ( ) ( ) − + − = n n n n x R = ( 1)! ( ) ( 1) + = + n R n n ( ) 0 R x − n − 0 ( ) Rn x0 − − 0 ( ) 0 ( ) R x n − n − 0 1 ( 在x0与x 之间) 2 ( 在x0与 1 之间) (在x0与 n 之间) ( 1)! ( ) ( 1) + = + n f n x 多 次 使 用 柯 西 中 值 定 理

>泰勒(Taylor)中值定理2 如果函数f(x)在x,的某个邻域U(x内具有(n+1)阶导数, 那么对任一x∈U(x),有 函 函数f)按x-x)的幂展开的 +R.( 带有拉格朗日余项的n阶泰勒公式 其中 R(x)= a)" 这里5是x与x之间的某个值
➢ 泰勒(Taylor)中值定理2 其中 这里 是 与 之间的某个值. 函数f (x)按(x-x0 )的幂展开的n次泰勒多项式 拉格朗日 余项 函数f (x)按(x-x0 )的幂展开的 带有拉格朗日余项的n阶泰勒公式 如果函数 在 的某个邻域 内具有 那么对任一 有 阶导数