西安电子科技大学：《数字信号处理》课程教学课件（讲稿）02 时域离散信号和系统的频域分析（2/2）

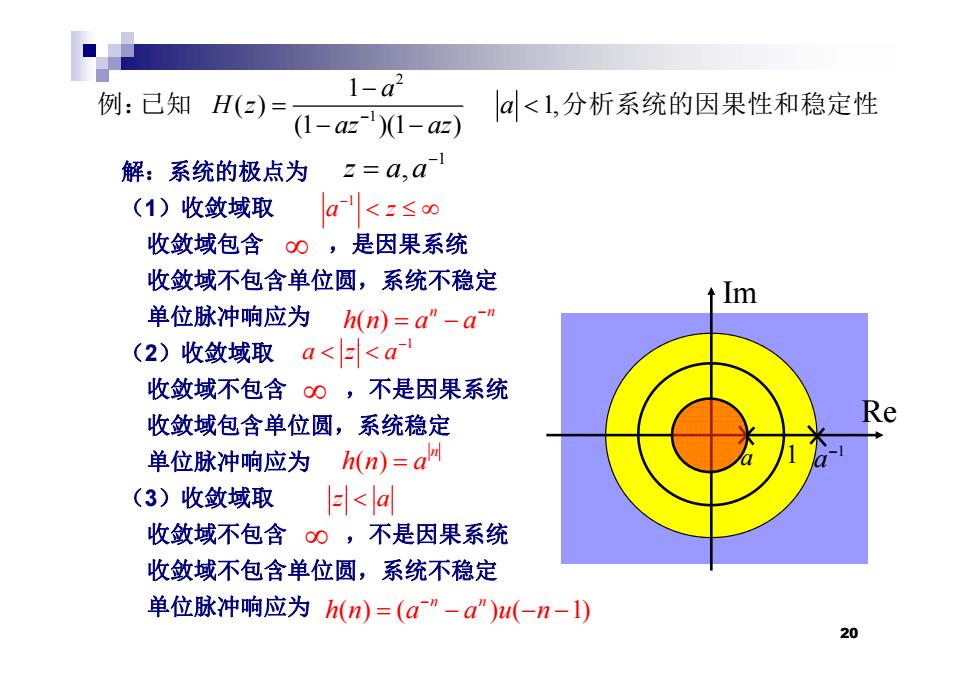
1-a2 例：已知H(z)= a<l,分析系统的因果性和稳定性 (1-az1)1-az) 解：系统的极点为 2=a,a (1)收敛域取 a <2≤00 收敛域包含 00，是因果系统 收敛域不包含单位圆，系统不稳定 tIm 单位脉冲响应为 h(n)=a”-a" (2)收敛域取a<<a 收敛域不包含00，不是因果系统 收敛域包含单位圆，系统稳定 Re 单位脉冲响应为 h(n)=a网 (3)收敛域取 <a 收敛域不包含00，不是因果系统 收敛域不包含单位圆，系统不稳定 单位脉冲响应为h(n)=(a"-a”)u(-n-1) 20

2 1 ( ) 1, a Hz a  例：已知   分析系统的因果性和稳定性 解：系统的极点为 1 ( ) 1, (1 )(1 ) Hz a az az     例：已知 分析系统的因果性和稳定性 1 z aa,   （1）收敛域取 收敛域包含 ，是因果系统 1 a z      收敛域不包含单位圆，系统不稳定 单位脉冲响应为 （2）收敛域取 Im ( ) n n hn a a   1 （2）收敛域取 收敛域不包含 ，不是因果系统 收敛域包含单位圆 系统稳定 Re 1 aza    收敛域包含单位圆，系统稳定 单位脉冲响应为 （3）收敛域取 1 a  ( ) a 1 n hn a  （3）收敛域取 z a  收敛域不包含 ，不是因果系统 收敛域不包含单位圆，系统不稳定 z a   单位脉冲响应为 ( ) ( ) ( 1) n n hn a a u n     20

2.4.3用Z变换求解系统的输出响应 ■递推法：已知差分方程、初始条件，递推求解差 分方程 ■卷积 ■Z变换： 口系统输出响应：零状态响应和零输入相应 稳态响应和暂态响应 Matlab 21

243 . . 用Z变换求解系统的输出响应 变换求解系统的输出响应  递推法：已知差分方程、初始条件，递推求解差 分方程  卷积  Z变换: 系统输出响应：零状态响应和零输入相应 稳态响应和暂态响应  M tl b a a 21

1.零状态响应与零输入响应 已知系统的N阶差分方程，输入信号x)是因果序列，系 统初始条件为y-1),y-2).,-): 0)=∑bxn-)-∑a(n-) ■系统的零状态响应和零输入响应？ 22

1.零状态响应与零输入响应  已知系统的N阶差分方程，输入信号x( ) n 是因果序列，系 统初始条件为y(-1),y(-2),.,y(-N). 0 1 () ( ) ( ) M N i i i i y n bx n i ay n i         系统的零状态响应和零输入响应？ 22

1.零状态响应与零输入响应 JW0）=2bxn-0）-立a0n-) ■移位序列的Z变换 ZTLy(n-myu(m)=yn-m)u(n)="yn-m)=* =0 20:=:“20:+0: =zye)+:W02 ZT[y(n-1]=z1Y(z)+y(-1) ZTLy(n-2]=z2Y(z)+zy(-1)+y(-2) ZTy(n-3)]=z3Y(z)+z2y(-1)+zy(-2)+y(-3) 23

1.零状态响应与零输入响应 () ( ) ( ) M N i i 1.零状态响应与零输入响应 y n bx n i a      y n i  移位序列的Z变换 0 1 () ( ) ( ) i i i i y y     0 [ ( ) ( )] ( ) ( ) ( ) n n n n ZT y n m u n y n m u n z y n m z             1 () () 0 () () () lm m l lm nml lm l lm yl z z yl z yl z                lm l lm   0 1 ( ) () mm l z Y z z yl z       1 ZT[ ( y n zYz 1)] ( ) ( y 1)     l m   2 1 32 1 [ ( )] ( ) ( ) [ ( 2)] ( ) ( 1) ( 2) y y ZT y n z Y z z y y        32 1 ZT y n z Y z z y z y y [ ( 3)] ( ) ( 1) ( 2) ( 3)          23

ZT[x(n-m)u(n]=zm[X(e）+∑x(0z]=zmX(z) ■系统的差分方程 24n-小=立am-0 ■Z变换 立：-20[e+0 26:Xe)-立a0-立aeye 克-xe)立a=20: .Y(z)= 24

1 [ ( ) ( )] [ ( ) ( ) ] m l ZT X l   ( ) m X   系统的差分方程 [ ( ) ( )] [ ( ) ( ) ] m l l m ZT xn mun z X z x l z       ( ) m  z X z  系统的差分方程 () () M N i i   bx n i a    y n i 0 0 () () i i i i y      Z变换 1 ( ) ( ) () M N i ii l bz X z a z Y z z y l z             0 0 ( ) ( ) () i i i i li bz X z a z Y z z y l z            MN N 1    00 0 ( ) () ( ) i ili ii i i i li i bz X z az y l z az Y z            M N 1 0 0 ( ) () ( ) i il i i i i li N N bz X z az y l z Y z             0 0 i i i i i i az az       24