
图14-3表示根据R、L、C元件时域电压电流的关系式如 何得到它们频域电路模型的过程。 in (t) R 拉氏变换 Ip(s) R 0☐0 +R(t) +U(s)- (a) (0) i(t)L 1 0 i(t) 拉氏变换h(s 电源变换 h(s)SL Lh() +4(t) m U(s) 十4(t) +U(s) Cuc(0) 1 c(0) ic(t)C ie(t) C ,4c(0) 拉氏变换(s) SC 电源变换 l(s) oHH +4c(t) uc(t) +U(s) (c) Ue(s) 图14-3 由此可见,在频域模型中电感电流和电容电压的初始 值是以一个阶跃电源或冲激电源的形式出现的
图14-3表示根据R、L、C元件时域电压电流的关系式如 何得到它们频域电路模型的过程。 图14-3 由此可见,在频域模型中电感电流和电容电压的初始 值是以一个阶跃电源或冲激电源的形式出现的

二、频域法分析线性时不变电路的主要步骤 (一)画出频域的电路模型 已知时域电路模型可以画出频域的电路模型,其步骤如下: 1.将时域模型中的各电压电流用相应的拉普拉斯变换表示 并标明在电路图上。 2.将R、L、C元件用图14-3所示频域等效电路模型表示。 其中,电感电流的初始值(0)是以阶跃电流源(0)s或冲激 电压源Li(0)的形式出现。电容电压的初始值4c(0)是以阶跃 电压源4c(O)/s或冲激电流源Cuc(0)的形式出现
二、频域法分析线性时不变电路的主要步骤 (一)画出频域的电路模型 已知时域电路模型可以画出频域的电路模型,其步骤如下: 1.将时域模型中的各电压电流用相应的拉普拉斯变换表示, 并标明在电路图上。 2.将R、L、C元件用图14-3所示频域等效电路模型表示。 其中,电感电流的初始值iL(0- )是以阶跃电流源iL(0- )/s或冲激 电压源LiL (0- )的形式出现。电容电压的初始值uC(0- )是以阶跃 电压源uC(0- )/s或冲激电流源CuC(0- )的形式出现

二)根据频域形式的KCL、KVL和元件VCR关系 建立频域的电路方程,并求解得到电压电流的拉普 拉斯变换。 (三)根据电压电流的拉普拉斯变换,用部分分式展开 和查拉普拉斯变换表的方法得到时域形式的电压和 电流
(二)根据频域形式的KCL、KVL和元件VCR关系, 建立频域的电路方程,并求解得到电压电流的拉普 拉斯变换。 (三)根据电压电流的拉普拉斯变换,用部分分式展开 和查拉普拉斯变换表的方法得到时域形式的电压和 电流
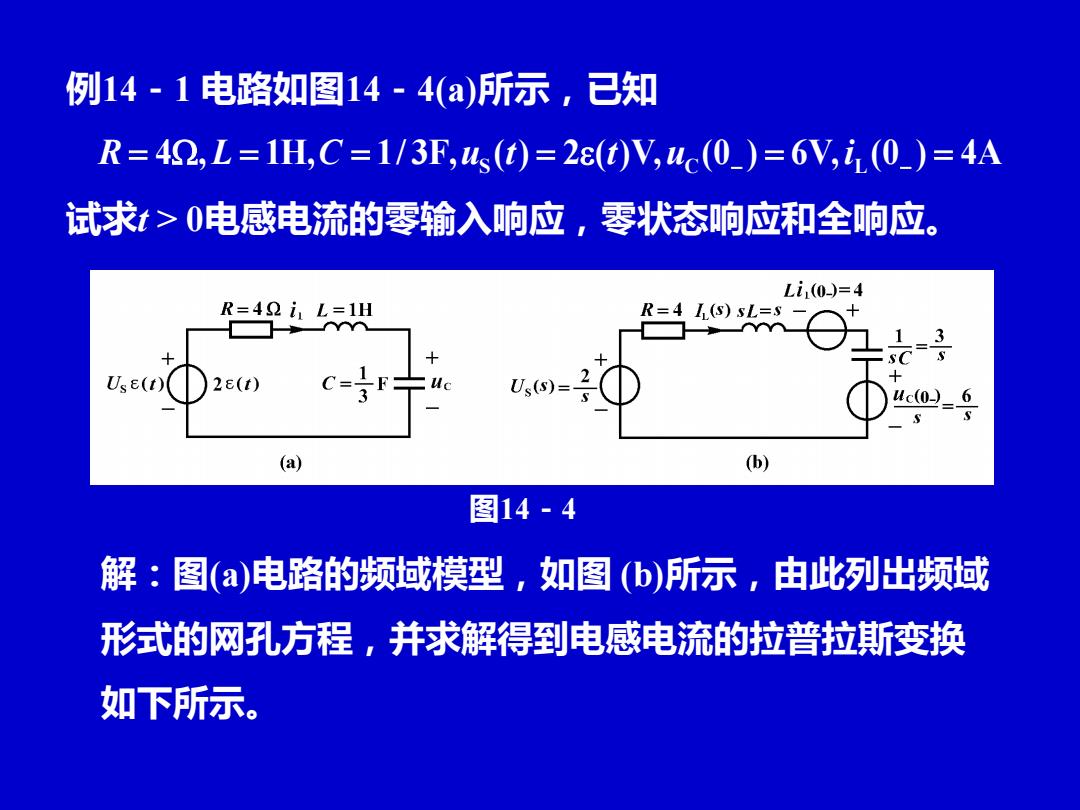
例14-1电路如图14-4(a)所示,已知 R=42,L=1H,C=1/3F,u(t)=2ε(t)V,uc(0)=6V,i(0_)=4A 试求t>0电感电流的零输入响应,零状态响应和全响应。 Li(0-)=4 R=42i1L=1H R=4 I(S)SL=S 门1=3 UsE(t) 2e(t) X Us(s)=- 4c(0=6 (a) (b) 图14-4 解:图(a)电路的频域模型,如图(b)所示,由此列出频域 形式的网孔方程,并求解得到电感电流的拉普拉斯变换 如下所示
例14-1 电路如图14-4(a)所示,已知 试求t > 0电感电流的零输入响应,零状态响应和全响应。 R = 4, L = 1H,C = 1/ 3F,uS (t) = 2(t)V, uC (0− ) = 6V, i L (0− ) = 4A 图14-4 解:图(a)电路的频域模型,如图 (b)所示,由此列出频域 形式的网孔方程,并求解得到电感电流的拉普拉斯变换 如下所示

Li1(0-)=4 R=4Q i L=1H R=4 I(s)sL=s {□13 X + UsE(t) 2e(t) C= 3F ,=2 + 4c02=6 (a) (b) 图14-4 U()+L元0.)-40 L4(0.)-40 I(S)= S S Us(s) 1 R+sL+ 1 R+sL+ sc R+sL+ sC 4s-6 2 4s-6 2 s2+4s+3s2+4s+3 (s+1)(s+3) (s+1)(s+3) G3G 全响应=零输入响应十 零状态响应
图14-4 ( 3) 1 ( 1) 1 ( 3) 9 ( 1) 5 ( ) ( 1)( 3) 2 ( 1)( 3) 4 6 4 3 2 4 3 4 6 1 ( ) 1 (0 ) (0 ) 1 (0 ) ( ) (0 ) ( ) 2 2 S C L C S L 全响应 = 零输入响应 + 零状态响应 + − + + + + + + − = + + + + + − = + + + + + − = + + + + + − = + + + − = − − − − s s s s I s s s s s s s s s s s sC R sL U s sC R sL s u Li sC R sL s u U s Li I s