h() A T 6) 图10-8 对于图b)所示半波整流波形,将其瞬时值表达式 h(t)=Asin @t (0<t<T/2) 代入式(10-4)中,可以得到半波整流波形的有效值是 振幅值的0.5倍,或者说其振幅值是有效值的2倍的结论, 具体计算过程如下: T/2 H 21 A2 sin2otdt 月I号-co2m--0 A .5A 2
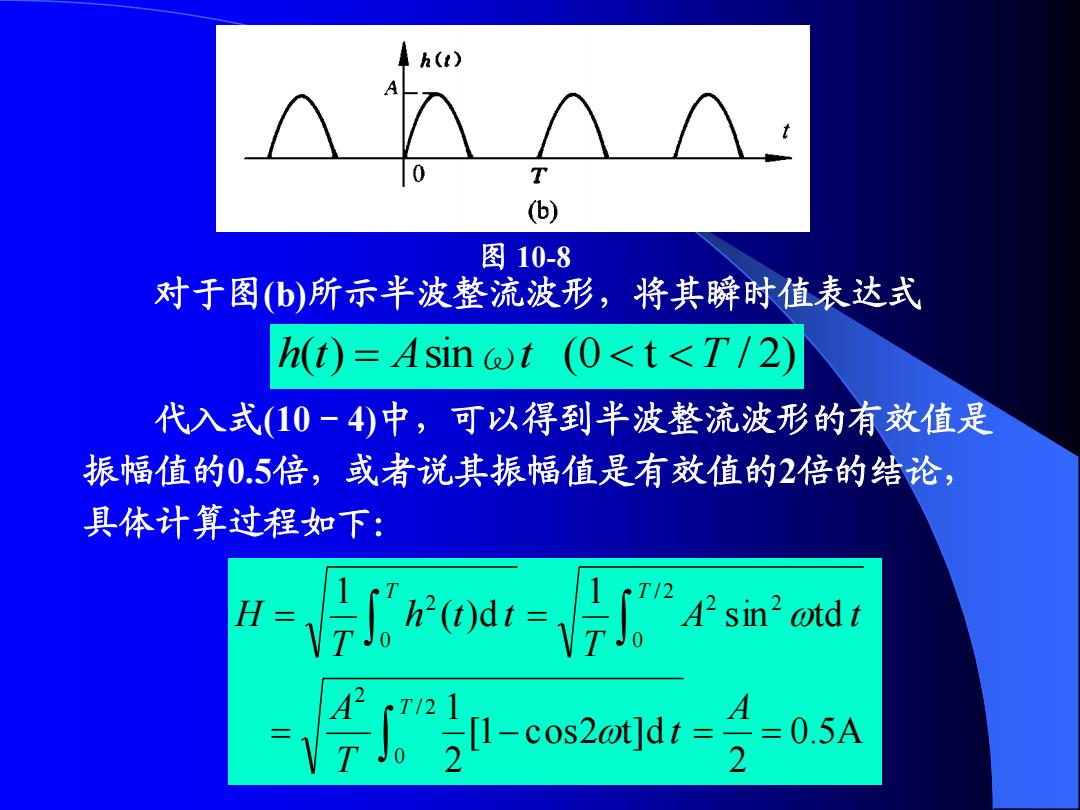
对于图(b)所示半波整流波形,将其瞬时值表达式 h(t) Asinωt (0 t T / 2) 代入式(10-4)中,可以得到半波整流波形的有效值是 振幅值的0.5倍,或者说其振幅值是有效值的2倍的结论, 具体计算过程如下: 0.5A 2 [1 cos2 t]d 2 1 sin td 1 ( ) d 1 / 2 0 2 / 2 0 2 2 0 2 A t T A A t T h t t T H T T T 图 10-8
§10-2正弦稳态响应 正弦电流激励的RC电路分析 我们现在讨论图10-9所示RC电路,电路原来已经达到 稳定状态,在=0时刻断开开关,正弦电流i()户IsmC0s(o 什必)作用于RC电路,求电容电压山(①)的响应。 十 图10-9
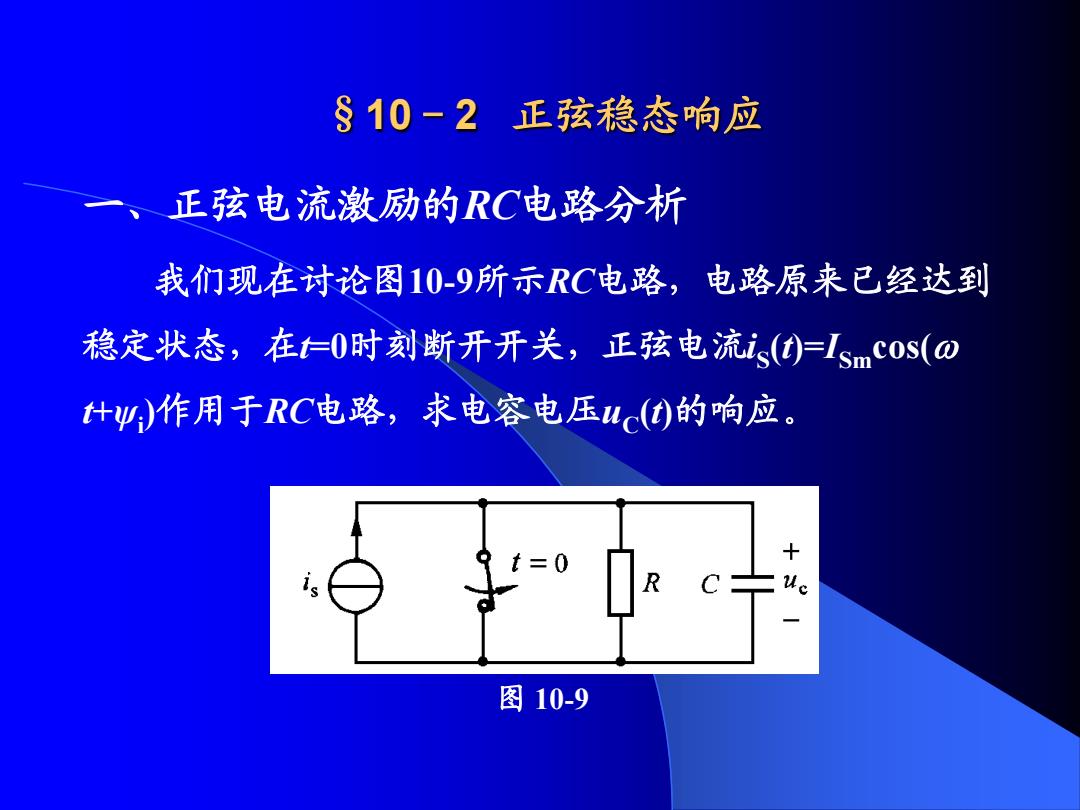
§10-2 正弦稳态响应 一 、正弦电流激励的RC电路分析 图 10-9 我们现在讨论图10-9所示RC电路,电路原来已经达到 稳定状态,在t=0时刻断开开关,正弦电流i S (t)=I Smcos( t+ψi )作用于RC电路,求电容电压uC (t)的响应

首先建立>0电路的微分方程如下: dtc+ uc =Ism cos(ot+v) t≥0 (10-7) dt R 对应齐次微分方程的通解uch()为 uch (t)=Kes=Ke RC 微分方程特解4c,)的形式与电流源相同,为同一频率 的正弦时间函数,即 ucp (t)=Ucm cos(@t+)
首先建立t>0电路的微分方程如下: cos( ) 0 (10 7) 1 d d C Sm i C u I t t t R u C 对应齐次微分方程的通解uCh(t)为 RC t st uCh (t) Ke Ke 微分方程特解uCp(t)的形式与电流源相同,为同一频率 的正弦时间函数,即 ( ) cos( ) Cp Cm u u t U t

4cp()=Ucm cos(ot+Wu) 为了确定Ucm和叫.,可以将上式代入微分方程中 duc+ uc =I'sm cos(ot+) t≥0 (10-7) dt R @CUcmsin(at+)+Ucm cos@t+)=Ism cosot+;) R 求解得到 Cm (10-8) Vo2C2+(1/R)2 Ψu=W,-arctan @CR) (10-9)
为了确定UCm和ψu,可以将上式代入微分方程中 求解得到 arctan( ) (10 9) (10 8) (1/ ) u i 2 2 2 Sm Cm CR C R I U cos( ) 0 (10 7) 1 d d C Sm i C u I t t t R u C cos( ) cos( ) 1 sin( ) Cm u Cm u Sm i U t I t R CU t ( ) cos( ) Cp Cm u u t U t

微分方程的完全解为 uc(t)=Ke Rc +Ucm cos(@t+) (t≥0)》 (10-10) 可以求得 K=uc(0)-Ucm cosyu 最后得到电容电压4c()的全响应为 uc(t)=[uc(0)-Ucm cosw]e Rc+Ucm c os(ot+Ψu) (t≥0)》 暂态响应 正弦稳态响应 (10-11)》
微分方程的完全解为 (10 10) ( ) e cos( ) ( 0) C Cm u u t K U t t RC t 可以求得 C Cm u K u (0) U cos 最后得到电容电压uC (t)的全响应为 (10 11) ( ) [ (0) cos ] e cos( ) ( 0) C C Cm u Cm u u t u U U t t R C t 暂态响应 正弦稳态响应