本电路的初始条件为零,属于零状态响应,所画出的 波形如图所示。曲线1表示通解,它是电路的自由响应,当 RC>0的条件下,它将随着时间的增加而按指数规律衰减到 零,称为暂态响应。曲线2表示特解,它按照正弦规律变化, 其角频率与激励电源的角频率相同,当暂态响应衰减完后, 它就是电路的全部响应,称为正弦稳态响应。 uc(t) -Uemcosψu 图10-10
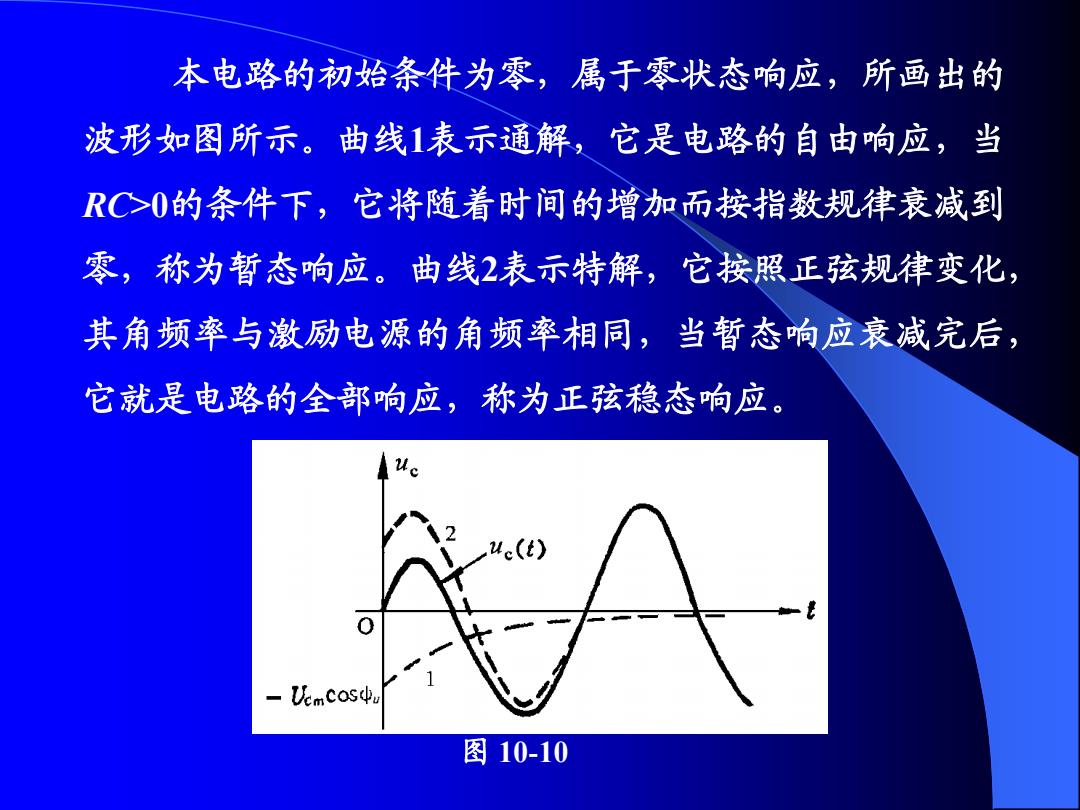
本电路的初始条件为零,属于零状态响应,所画出的 波形如图所示。曲线1表示通解,它是电路的自由响应,当 RC>0的条件下,它将随着时间的增加而按指数规律衰减到 零,称为暂态响应。曲线2表示特解,它按照正弦规律变化, 其角频率与激励电源的角频率相同,当暂态响应衰减完后, 它就是电路的全部响应,称为正弦稳态响应。 图 10-10

二、 用相量法求微分方程的特解 求解正弦电流激励电路全响应的关键是求微分方程的 特解。假如能用相量来表示正弦电压电流,就可以将常系 数微分方程转变为复系数的代数方程,便于使用各种计算 工具。现将这种相量法介绍如下: is(t)=Ism cost+)=Re(ismej) ucp(t)=Ucm cosot+)=Re(Ucme) 代入微分方程 C dt [Recm]+Re(cmei)=Re(isme) R
二、 用相量法求微分方程的特解 ( ) cos( ) Re( e ) ( ) cos( ) Re( e ) j Cp Cm u Cm j S Sm i Sm t t u t U t U i t I t I 求解正弦电流激励电路全响应的关键是求微分方程的 特解。假如能用相量来表示正弦电压电流,就可以将常系 数微分方程转变为复系数的代数方程,便于使用各种计算 工具。现将这种相量法介绍如下: 代入微分方程 Re( e ) Re( e ) R 1 [Re( e ) ] d d j Sm j Cm j Cm t t t U U I t C

取实部与微分运算的次序交换 Re[(joCU)]+-。Re(Ucm)=Re(isne) R ReljC+Re( 由于方程在任何时刻相等,其方程的复数部分应该相 等,由此得到一个复系数的代数方程 (joC+Ucm=isn (10-12) 求解此代数方程得到电容电压相量为 Sm Cm j@C+1/R =Ucm∠u
取实部与微分运算的次序交换 ) e ] Re( e ) 1 Re[( j Re( e ) Re( e ) 1 Re[( j e ) ] j Sm j Cm j Sm j Cm j Cm t t t t t U I R C U I R CU + 由于方程在任何时刻相等,其方程的复数部分应该相 等,由此得到一个复系数的代数方程 ) (10 12) 1 ( j UCm ISm R C 求解此代数方程得到电容电压相量为 Cm u Sm Cm j 1/ U C R I U

电容电压的振幅和初相分别为 Sm Cm Vo2C2+(1/R) Ψu=y:-arc tan(oCR) 这与式(10-8)和(10-9)完全相同。计算出电容电压的 振幅和初相,就能够写出稳态响应 ucp (t)=Ucm cos(at+)
电容电压的振幅和初相分别为 2 2 2 Sm Cm C (1/ R) I U arc tan( ) u i CR 这与式(10-8)和(10-9)完全相同。计算出电容电压的 振幅和初相,就能够写出稳态响应 ( ) cos( ) Cp Cm u u t U t

从以上叙述可知,用相量表示正弦电压电流后,可将 微分方程转换为复系数代数方程,求解此方程得到特解的 相量后,易于写出正弦稳态响应的瞬时值表达式。 我们可以将以上求特解的方法推广到一般情况,对于 由正弦信号激励的任意线性时不变动态电路,先写出阶 常系数微分电路,再用相量表示同频率的各正弦电压电流, 将微分方程转变为复系数代数方程,再求解代数方程得到 电压电流相量,就能写出特解的瞬时值表达式
从以上叙述可知,用相量表示正弦电压电流后,可将 微分方程转换为复系数代数方程,求解此方程得到特解的 相量后,易于写出正弦稳态响应的瞬时值表达式。 我们可以将以上求特解的方法推广到一般情况,对于 由正弦信号激励的任意线性时不变动态电路,先写出n阶 常系数微分电路,再用相量表示同频率的各正弦电压电流, 将微分方程转变为复系数代数方程,再求解代数方程得到 电压电流相量,就能写出特解的瞬时值表达式