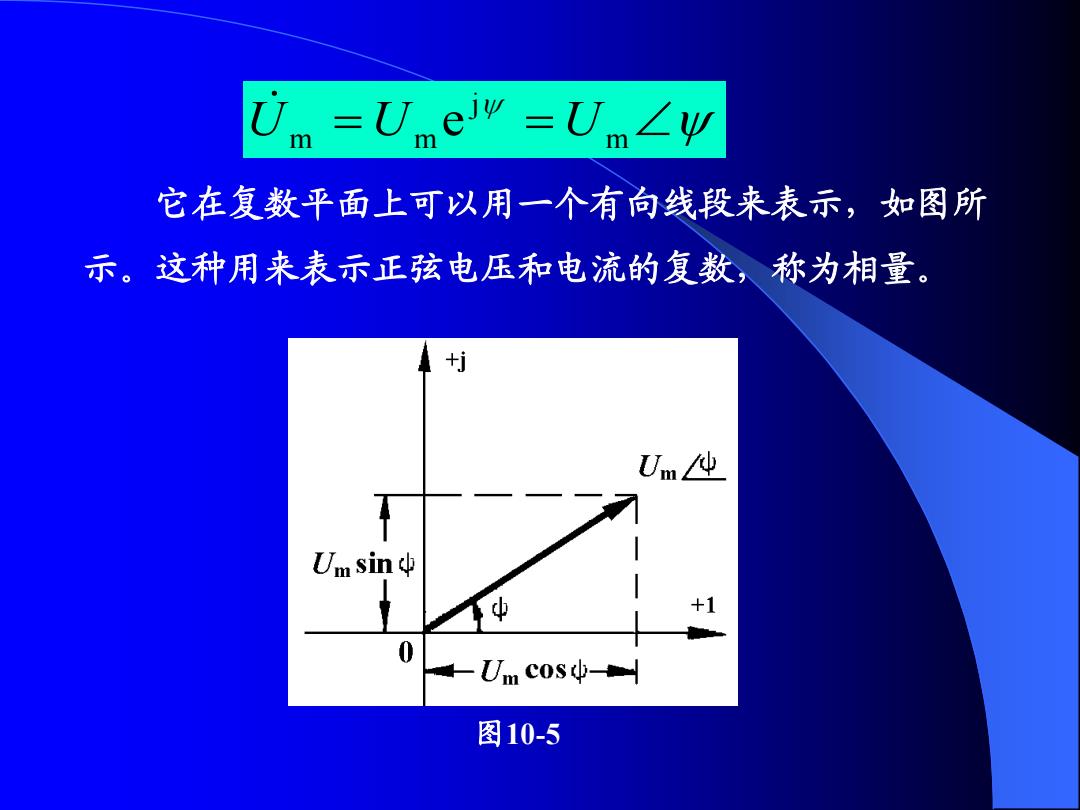
m =Umew=Um∠w m 它在复数平面上可以用一个有向线段来表示,如图所 示。这种用来表示正弦电压和电流的复数,称为相量。 ti Um Um sin中 +1 0 -Um cosψ 图10-5
它在复数平面上可以用一个有向线段来表示,如图所 示。这种用来表示正弦电压和电流的复数,称为相量。 图10-5 m j m m U U e U

设想电压相量以角速度ω沿反时针方向旋转,它在 实轴投影为 十 im[0n包l Umsin(@+p) 1=1Um Loot Usinp U cos(@t+y), t=0 在虚轴上投影 Umcos 为msin(ot+), Umcos(@1+) 角速度ω 它们都是时间 的正弦函数 如图所示。 图10-6旋转相量及其在实轴和虚轴上的投影
设想电压相量以角速度ω沿反时针方向旋转,它在 实轴投影为 Um cos(t+ψ), 在虚轴上投影 为Um sin(t+ψ), 它们都是时间 的正弦函数, 如图所示。 图10-6 旋转相量及其在实轴和虚轴上的投影

将电压相量 ☑m=Ume 与旋转因子 eia=cosattjsin@t 相乘可以得到以下数学表达式 Ume=Ume) =U cos(@t+y+j sin(@t+y)
将电压相量 ψ U U e j m m 与旋转因子 e jt=cost+jsin t 相乘可以得到以下数学表达式 cos( ) j sin( ) e e m m j ( ) m j t m U t ψ U t ψ U U t ψ

上式表明正弦电压与电压相量之间的关系为 Re[Ue]=Um cos@t+y) Imet]=U sin(@t+) 由此可得 u(t)=Um cos@t+) =Re(Uei)
上式表明正弦电压与电压相量之间的关系为 Im[ e ] sin( ) Re[ e ] cos( ) m j t m m j t m U U t ψ U U t ψ ω ω 由此可得 Re( e ) ( ) cos( ) j m m t U u t U t ψ

由上述可见,一个随时间按正弦规律变化的电压和电 流,可以用一个称为相量的复数来表示。已知正弦电压电 流的瞬时值表达式,可以得到相应的电压电流相量。反过 来,已知电压电流相量,也能够写出正弦电压电流的瞬时 值表达式。即 ut)=U cos(ot+y)ko→Um=Um∠y i(t)=I cos(0t+W)←o→1m=Im∠y
由上述可见,一个随时间按正弦规律变化的电压和电 流,可以用一个称为相量的复数来表示。已知正弦电压电 流的瞬时值表达式,可以得到相应的电压电流相量。反过 来,已知电压电流相量,也能够写出正弦电压电流的瞬时 值表达式。即 m i m m i m u m m u ( ) cos( ) ( ) cos( ) i t I t I I u t U t U U