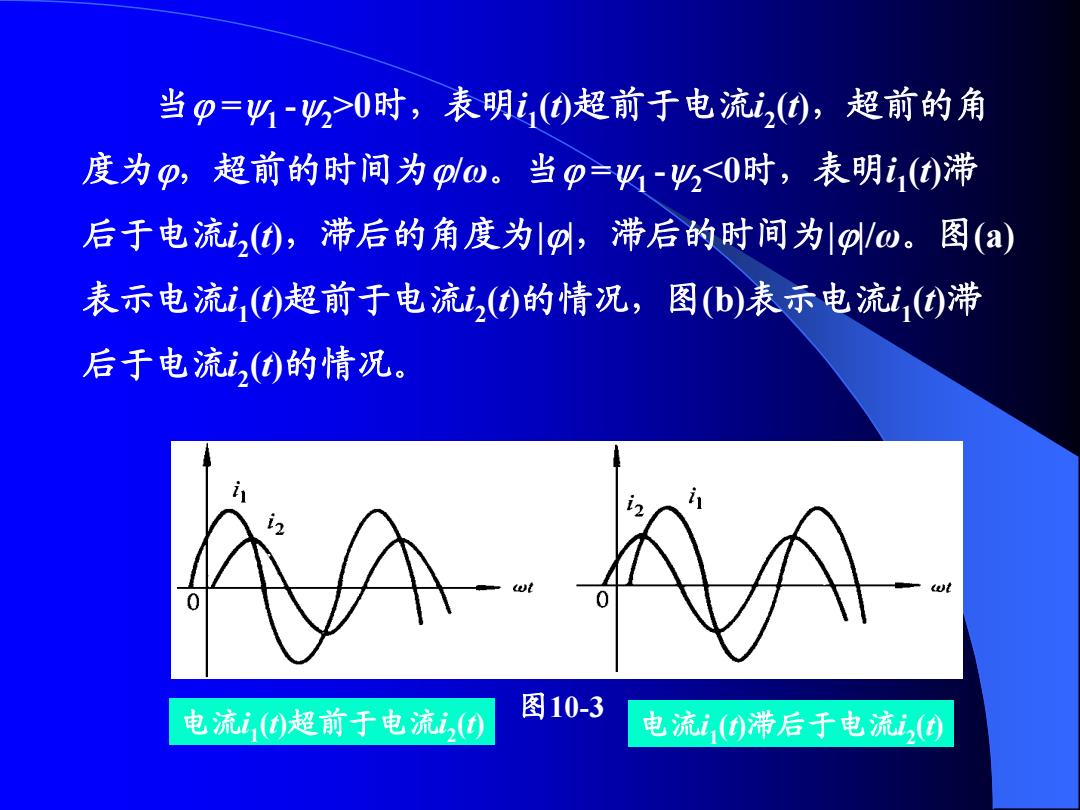
当p=%-当>0时,表明,()超前于电流i,0),超前的角 度为p,超前的时间为pω。当p=火1-%0时,表明i,()滞 后于电流i,①),滞后的角度为g,滞后的时间为g/w。图(a) 表示电流i,()超前于电流i,)的情况,图(b)表示电流i,()滞 后于电流i,()的情况 0 电流i,(0超前于电流i,() 图10-3 电流i,()滞后于电流i,()
电流i 1 (t)超前于电流i 2 (t) 电流i 1 (t)滞后于电流i 2 (t) 图10-3 当 =1 -2 >0时,表明i 1 (t)超前于电流i 2 (t),超前的角 度为,超前的时间为/ω。当 =1 -2 <0时,表明i 1 (t)滞 后于电流i 2 (t),滞后的角度为||,滞后的时间为||/ω。图(a) 表示电流i 1 (t)超前于电流i 2 (t)的情况,图(b)表示电流i 1 (t)滞 后于电流i 2 (t)的情况
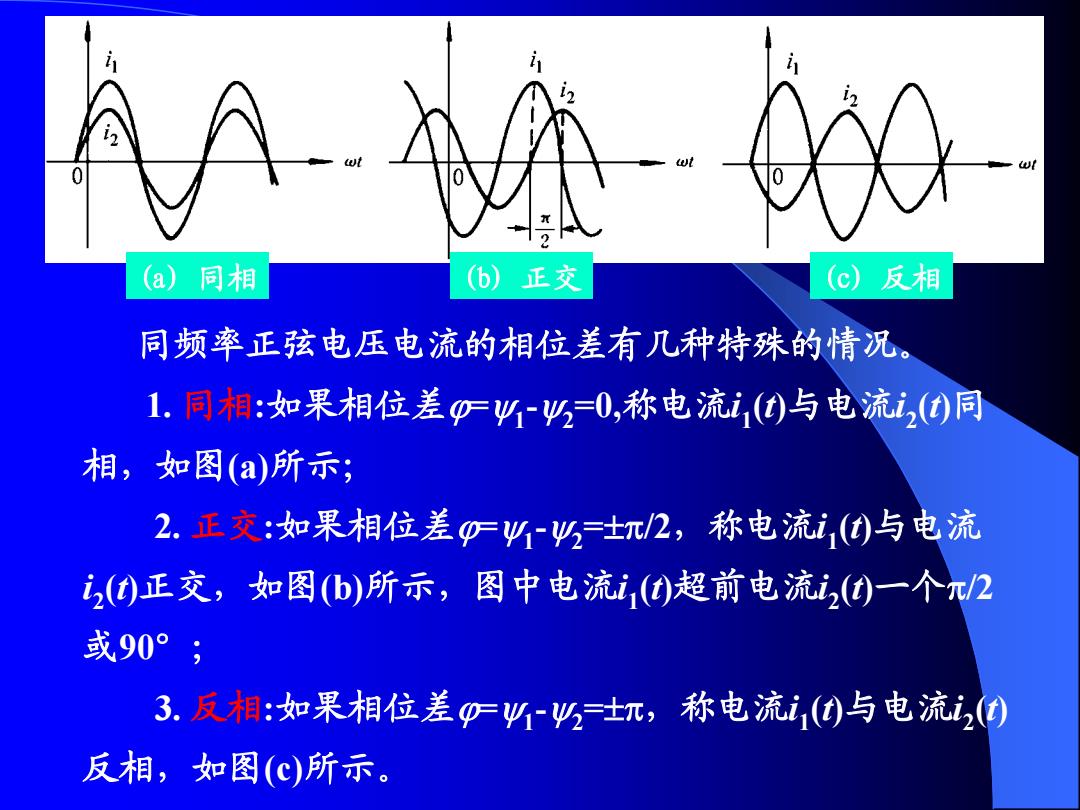
(a)同相 (b)正交 (c)反相 同频率正弦电压电流的相位差有几种特殊的情况。 1.同相:如果相位差巧0,称电流i,()与电流i2(同 相,如图(a)所示; 2.正交:如果相位差044,±元/2,称电流,(0与电流 20)正交,如图(b)所示,图中电流)超前电流,0一个π2 或90°; 3.反相:如果相位差4-4,±元,称电流i,()与电流2 反相,如图(c)所示
同频率正弦电压电流的相位差有几种特殊的情况。 1. 同相:如果相位差=1 -2 =0,称电流i 1 (t)与电流i 2 (t)同 相,如图(a)所示; 2. 正交:如果相位差=1 -2 =/2,称电流i 1 (t)与电流 i 2 (t)正交,如图(b)所示,图中电流i 1 (t)超前电流i 2 (t)一个/2 或90°; 3. 反相:如果相位差=1 -2 =,称电流i 1 (t)与电流i 2 (t) 反相,如图(c)所示。 (a) 同相 图(b) 10正交-4 (c) 反相

例10-2已知正弦电压u(t)和电流i),i2()的瞬时值表达式 为 u(t)=311 cos(@t-180)V i1(t)=5cos(ot-45°)A i2(t)=10 cos(@t+60)A 试求电压u()与电流i,()和i,()的相位差
例10-2 已知正弦电压u(t)和电流i 1 (t),i 2 (t)的瞬时值表达式 为 ( ) 10 cos( 60 ) A ( ) 5cos( 45 ) A ( ) 311 cos( 180 ) V 2 1 i t t i t t u t t 试求电压u(t)与电流i 1 (t)和i 2 (t)的相位差

(t)=311cos(ot-180°)V i1(t)=5cos(ot-45°)A i (t)=10 cos(@t+60)A 解:电压u(①)与电流i,(①的相位差为 0=(-180)-(-45)=-135 电压(t)与电流i,(t)的相位差为 0=(-180)-60°=-240 习惯上将相位差的范围控制在-180°到+180°之间, 我们不说电压(t)与电流i,(0)的相位差为-240°,而说电压 (t)与电流i,(t)的相位差为(360°-240)=120°
(180 ) (45 ) 135 电压 u(t)与电流i 2 (t)的相位差为 (180) 60 240 习惯上将相位差的范围控制在 -180°到+180°之间, 我们不说电压u(t)与电流i 2 (t)的相位差为-240 ,而说电压 u(t)与电流i 2 (t)的相位差为(360-240)=120 。 解:电压u(t)与电流i 1 (t)的相位差为 ( ) 10 cos( 60 ) A ( ) 5cos( 45 ) A ( ) 311 cos( 180 ) V 2 1 i t t i t t u t t

三、正弦电压电流的相量表示 分析正弦稳态的有效方法是相量法,相量法的基础是 用一个称为相量的向量或复数来表示正弦电压和电流。假 设正弦电压为 u(t)=U cos(at+y) 利用它的振幅U和初相w来构成一个复数,复数的模 表示电压的振幅,其幅角表示电压的初相,即 Um=Umew=Um∠
三、正弦电压电流的相量表示 ( ) cos( ) u t U m t 利用它的振幅Um和初相ψ来构成一个复数,复数的模 表示电压的振幅,其幅角表示电压的初相,即 m j m m U U e U 分析正弦稳态的有效方法是相量法,相量法的基础是 用一个称为相量的向量或复数来表示正弦电压和电流。假 设正弦电压为