
i(t)=Im cos(ot+Ψ:) 10-1) 由于已知振幅1m,角频率0和初相, 就能够完全确 定一个正弦电流,称它们为正弦电流的三要素。与正弦电 流类似,正弦电压的三要素为振幅Um,角频率o和初相少, 其函数表达式为 u(t)=Um os(at+v) (10-2) 由于正弦电压电流的数值随时间变化,它在任一时刻 的数值称为瞬时值,因此式(10-1)和(10-2)又称为正弦电 流和正弦电压的瞬时值表达式
由于已知振幅Im ,角频率ω和初相i,就能够完全确 定一个正弦电流,称它们为正弦电流的三要素。与正弦电 流类似,正弦电压的三要素为振幅Um,角频率ω和初相u, 其函数表达式为 ( ) cos( ) (10 2) u t U m t u - 由于正弦电压电流的数值随时间t变化,它在任一时刻 的数值称为瞬时值,因此式(10-1)和(10-2)又称为正弦电 流和正弦电压的瞬时值表达式。 ( ) cos( ) 10 1) i t I m t i ( -

例10-1已知正弦电压的振幅为10伏,周期为100ms,初相为 π6。试写出正弦电压的函数表达式和画出波形图。 解:先计算正弦电压的角频率 2π T 2π =20m≈62.8rad/s 100x10-3
例10-1 已知正弦电压的振幅为10伏,周期为100ms,初相为 /6。试写出正弦电压的函数表达式和画出波形图。 20 62.8rad/s 100 10 2 2 3 T 解:先计算正弦电压的角频率
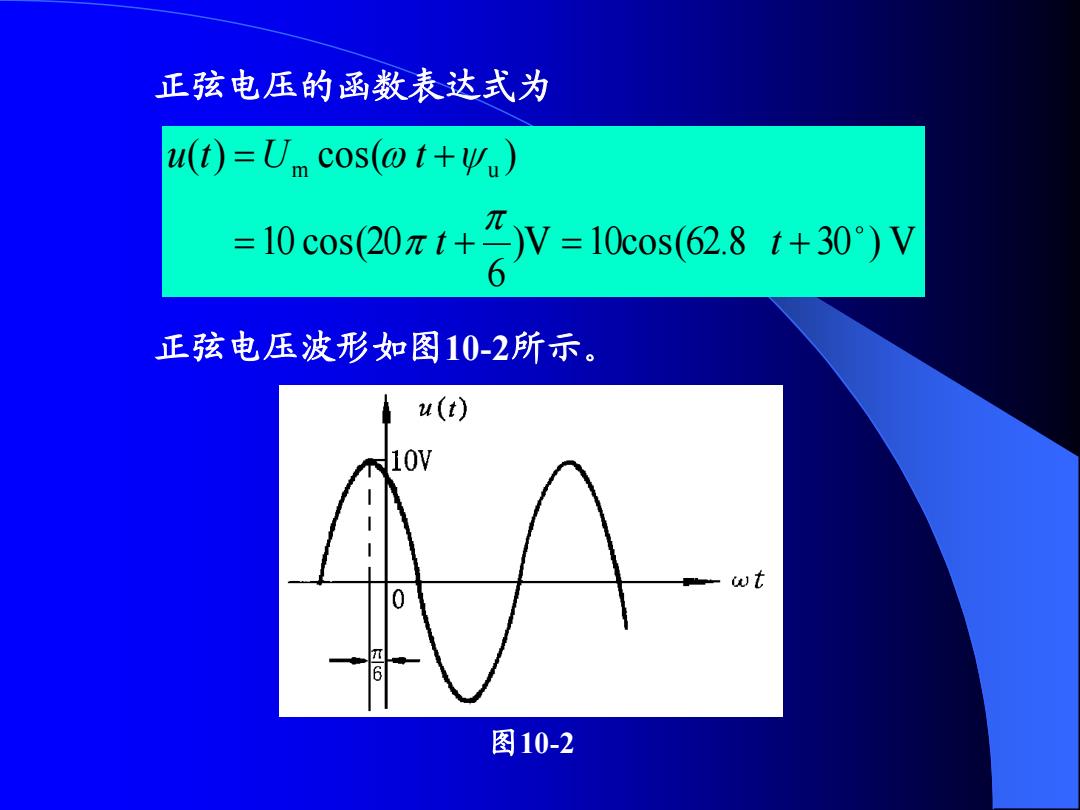
正弦电压的函数表达式为 u()=Um cos(ot+y.)) =10cos(20zt+)V=10cos(62.8t+30°)V 6 正弦电压波形如图10-2所示。 u(t) 10V ωt 0 6 图10-2
正弦电压的函数表达式为 )V 10cos(62.8 30 ) V 6 10 cos(20 ( ) cos( ) m u t t u t U t 正弦电压波形如图10-2所示。 图10-2

二、同频率正弦电压电流的相位差 正弦电流电路中,各电压电流都是频率相同的正弦量, 我们分析这些电路时,常常需要将这些正弦量的相位进行 比较。两个正弦电压电流相位之差,称为相位差,用表 示。例如有两个同频率的正弦电流 i (t)=Iim cos(ot+v) i2(t)=I2 cos(@t+w2) 电流i,()与电流i,()之间的相位差为 p=(0t-w)-(0t-w2)=必1-Ψ2 (10-3)
二、同频率正弦电压电流的相位差 ( ) cos( ) ( ) cos( ) 2 2m 2 1 1m 1 i t I t i t I t 正弦电流电路中,各电压电流都是频率相同的正弦量, 我们分析这些电路时,常常需要将这些正弦量的相位进行 比较。两个正弦电压电流相位之差,称为相位差,用表 示。例如有两个同频率的正弦电流 电流i 1 (t)与电流i 2 (t)之间的相位差为 ( ) ( ) (10 3) t 1 t 2 1 2

=(ot-v)-(ot-v2)=v-V2 (10-3) 上式表明两个同频率正弦量在任意时刻的相位差均等 于它们初相之差,与时间t无关。相位差的量值反映出电 流i,(①)与电流i,①)在时间上的超前和滞后关系 0>0 图10-3 p<0
上式表明两个同频率正弦量在任意时刻的相位差均等 于它们初相之差,与时间t无关。相位差的量值反映出电 流i 1 (t)与电流i 2 (t)在时间上的超前和滞后关系。 ( ) ( ) (10 3) t 1 t 2 1 2 0 图10-3 0