
电流密度 在导体中取一截面S,若在时间△t内流过该截面的总电荷为△q, 则通过该截面的电流强度定义为: I=lim Ag=dq △-0△tdt 一电流强度通常简称为电流,单位:安培(A) 一当导线横向尺寸可忽略时,电流称为线电流,对于线电流用 电流强度来描述就足够了。 一当导体的横向尺寸不能忽略时,应该认为电流分布在整个导 体的截面上,这种电流称为体电流: 一如果电流在一个厚度可忽略的导体曲面上流动,则称之为面 电流。 lexu@mail.xidian.edu.cn 6
电流密度 • 在导体中取一截面S,若在时间△t内流过该截面的总电荷为△q, 则通过该截面的电流强度定义为: – 电流强度通常简称为电流,单位:安培(A) – 当导线横向尺寸可忽略时,电流称为线电流,对于线电流用 电流强度来描述就足够了。 – 当导体的横向尺寸不能忽略时,应该认为电流分布在整个导 体的截面上,这种电流称为体电流; – 如果电流在一个厚度可忽略的导体曲面上流动,则称之为面 电流。 dt d q t q I t = ∆ ∆ = ∆ →0 lim lexu@mail.xidian.edu.cn 6
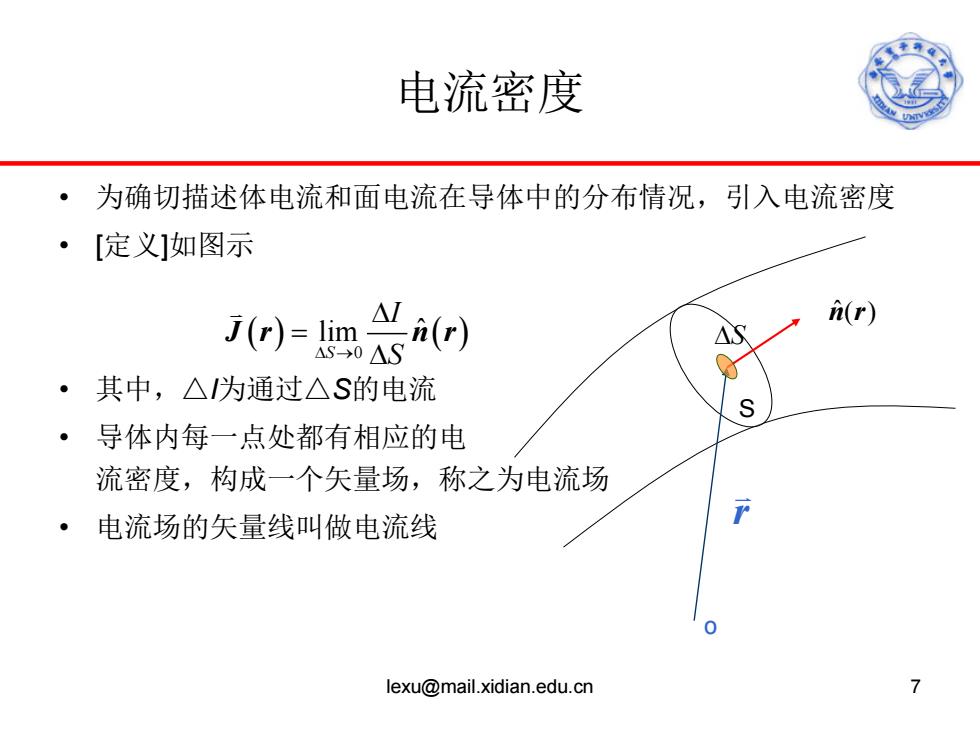
电流密度 ·为确切描述体电流和面电流在导体中的分布情况,引入电流密度 ·[定义]如图示 △ J(r)=lim i(r) (r) △S △S-0△S ·其中,△为通过△S的电流 S ·导体内每一点处都有相应的电 流密度,构成一个矢量场,称之为电流场 ·电流场的矢量线叫做电流线 lexu@mail.xidian.edu.cn >
电流密度 • 为确切描述体电流和面电流在导体中的分布情况,引入电流密度 • [定义]如图示 • 其中,△I为通过△S的电流 • 导体内每一点处都有相应的电 流密度,构成一个矢量场,称之为电流场 • 电流场的矢量线叫做电流线 S n r ˆ( ) r o ( ) ( ) ∆S 0 lim ˆ S I ∆ → S ∆ = ∆ Jr nr lexu@mail.xidian.edu.cn 7

电流密度 ·流过截面的电流就是J对S的通量 1=1 j.ds ·对于面电流,则定义 Js(F)=lim ALi() △1-→0△1 ·通过任意曲线的面电流为: 41 n(r) 1,=∫1J,×d1 lexu@mail.xidian.edu.cn 8
电流密度 • 流过截面的电流就是J对S的通量 • 对于面电流,则定义 • 通过任意曲线l的面电流为: ∫ = ⋅ S I J dS ( ) n (r) l I J r l S ∆ ∆ = ∆ →0 lim | | s s l I J dl = × ∫ lexu@mail.xidian.edu.cn 8
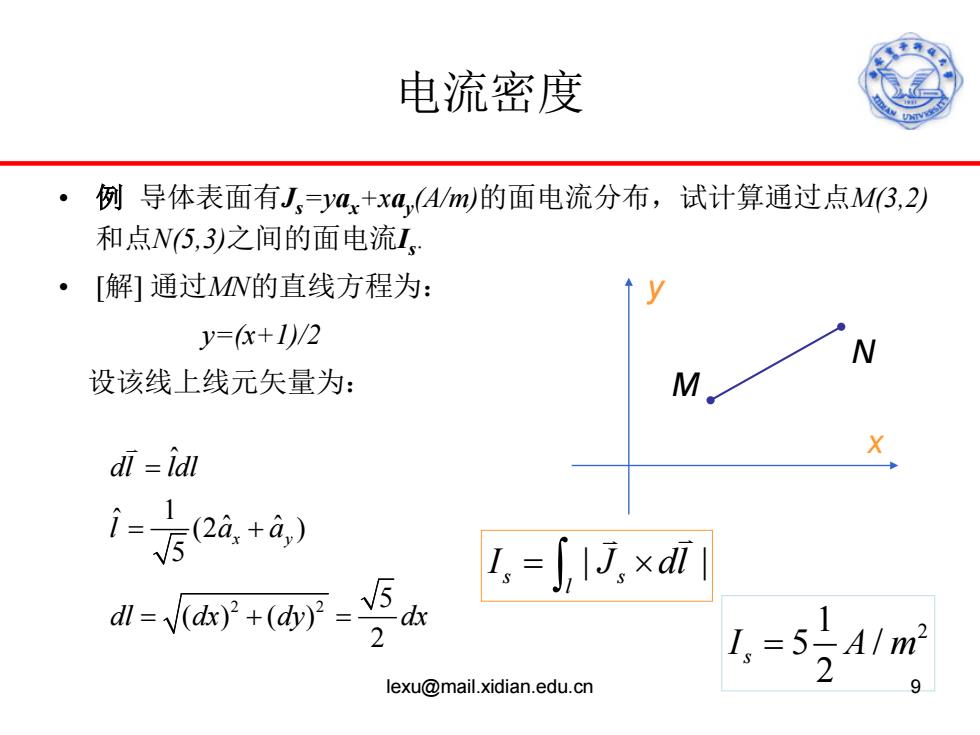
电流密度 ·例导体表面有J,=ya+xa,A/m的面电流分布,试计算通过点M(3,2) 和点N5,3)之间的面电流L ·[解]通过MW的直线方程为: y=(x+1)/2 N 设该线上线元矢量为: M X dl idl 1=1 52a,+a,) 1,=∫1J,×ai d-Ndx)+(avy-dx 1=5A/m2 2 lexu@mail.xidian.edu.cn
电流密度 • 例 导体表面有Js=yax+xay(A/m)的面电流分布,试计算通过点M(3,2) 和点N(5,3)之间的面电流Is. • [解] 通过MN的直线方程为: y=(x+1)/2 设该线上线元矢量为: M N x y 2 2 ˆ 1 ˆ (2 ) ˆ ˆ 5 5 () () 2 x y dl ldl l aa dl dx dy dx = = + = += | | s s l I J dl = × ∫ 1 2 5 / 2 s I Am = lexu@mail.xidian.edu.cn 9
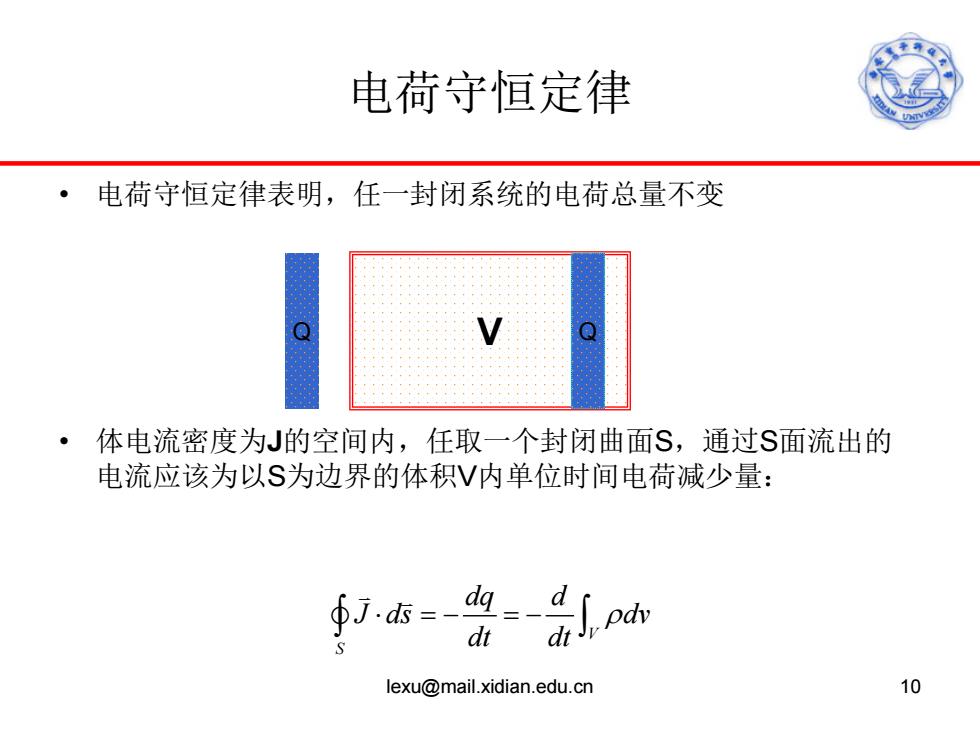
电荷守恒定律 ·电荷守恒定律表明,任一封闭系统的电荷总量不变 ·体电流密度为J的空间内,任取一个封闭曲面S,通过S面流出的 电流应该为以S为边界的体积V内单位时间电荷减少量: ∮75=-9 lexu@mail.xidian.edu.cn 10
电荷守恒定律 • 电荷守恒定律表明,任一封闭系统的电荷总量不变 • 体电流密度为J的空间内,任取一个封闭曲面S,通过S面流出的 电流应该为以S为边界的体积V内单位时间电荷减少量: Q V Q V S dq d J ds dv dt dt ⋅ =− =− ρ ∫ ∫ lexu@mail.xidian.edu.cn 10