
三、瑞典条分法瑞典条分法假定滑动面是一个圆弧面并忽略条块间作用力对边坡整体稳定性的影响。11
11 三、瑞典条分法 ◼ 瑞典条分法假定滑动面是一个圆弧面, 并忽略条块间作用力对边坡整体稳定性 的影响
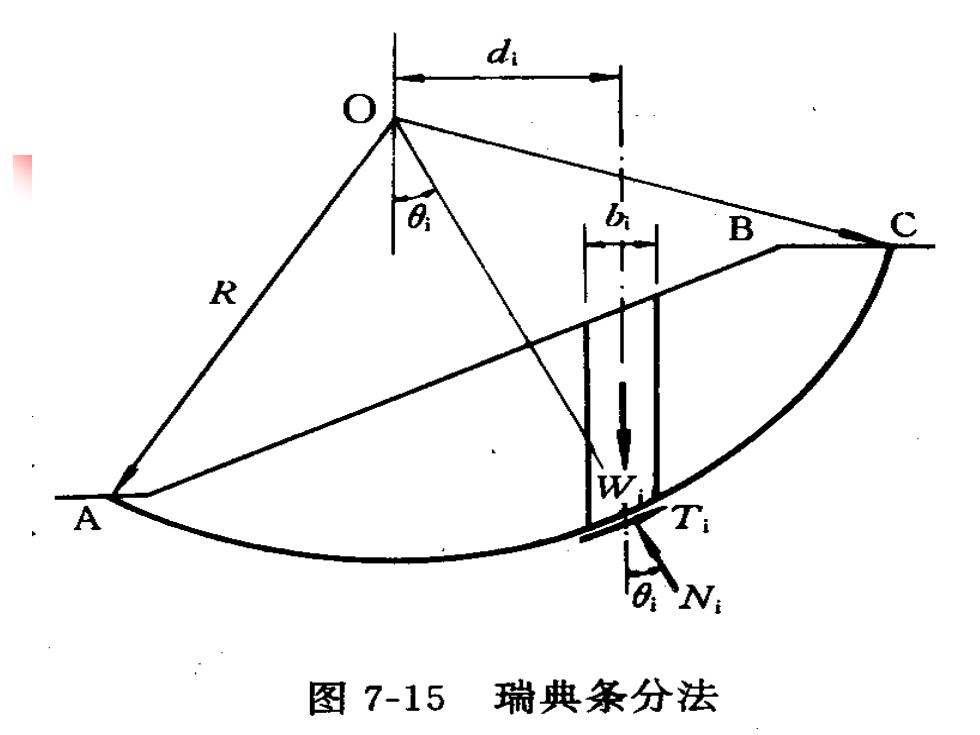
d;06.ABRWAON图7-15瑞典条分法
12

取条块进行分析(图7-15)根据径向力的平衡条件有(7-9)N, = W, cos O,>根据滑弧面上极限平衡条件有Tf_ cl, + N,tgd,(7-10)T =FsF式中,T一条块在滑动面上的抗剪强度;Fs一滑动圆弧的安全系数。13
13 ◼ 取条块i进行分析(图7-15 )。 ➢ 根据径向力的平衡条件有 ➢ 根据滑弧面上极限平衡条件有 式中,Tfi—条块i在滑动面上的抗剪强度; Fs—滑动圆弧的安全系数。 cos (7 -9) Ni =Wi i (7 -10) s i i i i s f i i F c l N t g F T T + = =

>式(7一10)中T±W,sinθ,因此条块的力多边形不闭合,即本法不满足条块的静力平衡条件。14
14 ➢ 式(7-10)中 ,因此条块的 力多边形不闭合,即本法不满足条块的 静力平衡条件。 Ti Wi i sin

按整体力矩平衡条件,外力对圆心力矩之和为零。>重力W.产生滑动力矩为Ewd, =w,Rsin 0,(7-11)>滑动面上抗滑力产生的抗滑力矩为ZTR=ZCl+Nigd.R(7-12)F因为整体力矩平衡,所以有ZWd,=ZTR(7-13)15
15 ◼ 按整体力矩平衡条件,外力对圆心力矩 之和为零。 ➢ 重力Wi产生滑动力矩为 ➢ 滑动面上抗滑力产生的抗滑力矩为 ◼ 因为整体力矩平衡,所以有 = sin (7 -11) Wi di Wi R i • + = R (7 -12) F c l N t g T R s i i i i i W d =T R (7 -13) i i i