西安电子科技大学：《数字信号处理》课程教学课件（讲稿）06 IIR数字滤波器（IIRDF）设计

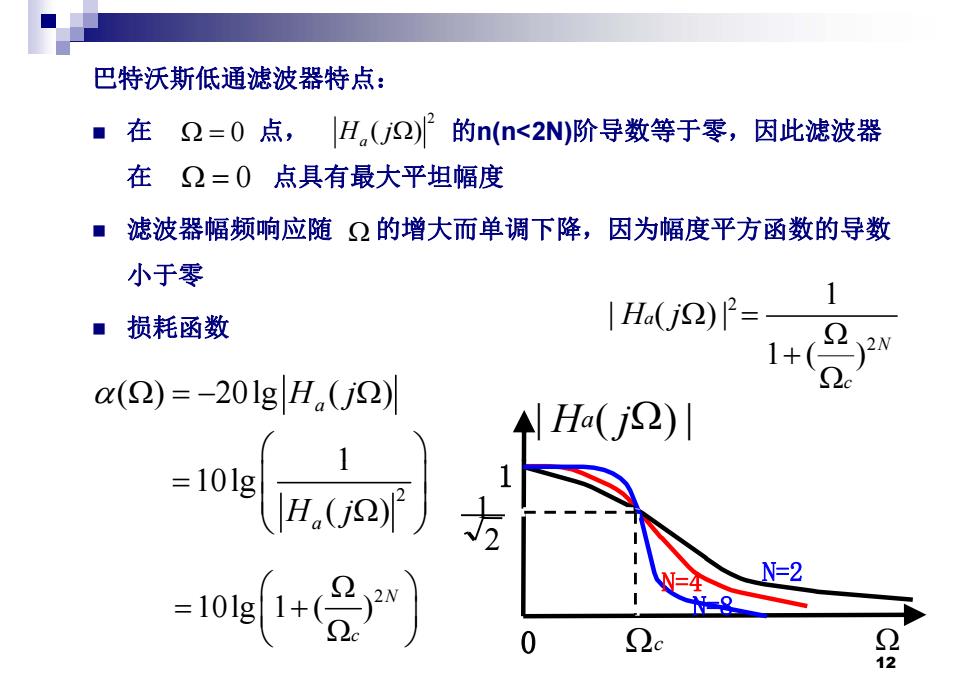
巴特沃斯低通滤波器特点： ■在2=0点，|H,(j2)2的n(n<2N阶导数等于零，因此滤波器 在Ω=0点具有最大平坦幅度 ■滤波器幅频响应随2的增大而单调下降，因为幅度平方函数的导数 小于零 ■损耗函数 |Ha(j)= 2 1+( (2)=-201gH(j2 H(j2)川 =101g H.U N=2 12

巴特沃斯低通滤波器特点：  在 点， 的   0 n(n<2N)阶导数等于零，因此滤波器 2 ( ) H j a  在 点具有最大平坦幅度  滤波器幅频响应随 的增大而单调下降 因为幅度平方函数的导数   0  滤波器幅频响应随  的增大而单调下降，因为幅度平方函数的导数 小于零  2 1 | ( )| H j  损耗函数 ( ) 20l ( )   H j 2 2 | ( )| 1( ) a N c H j     | Ha( j) | ( ) 20lg ( ) 1     H j a      c 2 1 1 2 1 10lg ( ) H j a          2 N=8 N=4 N=2 2 10lg 1 ( )    N     12 c  N 8 0 10lg 1 ( ) c      

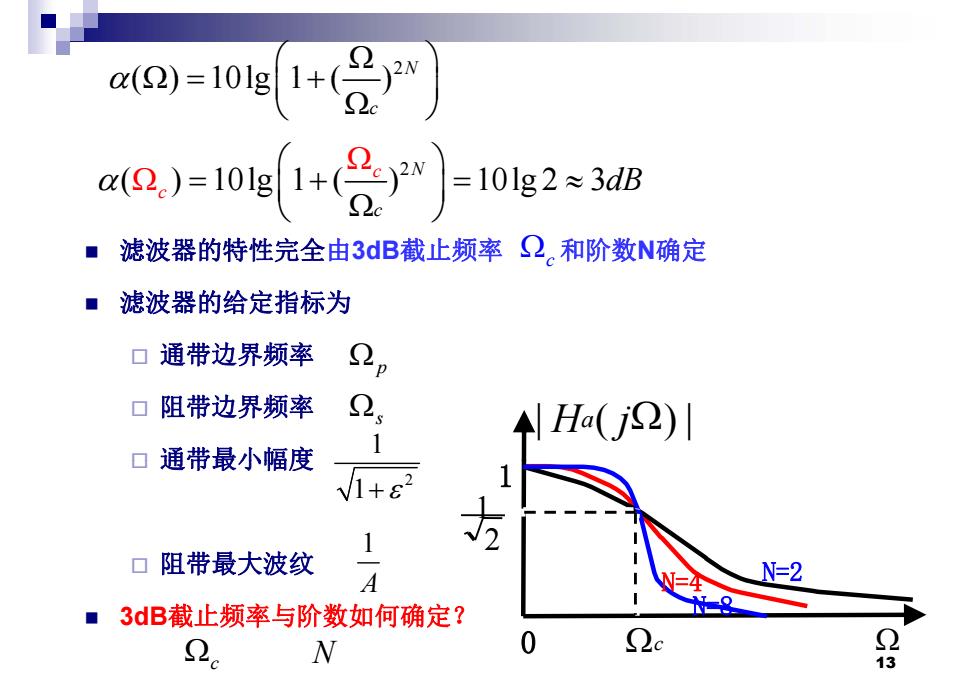
a(2)=10lg +产 =10lg2≈3dB ■滤波器的特性完全由3dB截止频率2，和阶数N确定 ■滤波器的给定指标为 口通带边界频率 p 口阻带边界频率 H(J2)川 口通带最小幅度 口阻带最大波纹 A N=2 ■3dB截止频率与阶数如何确定？ N 13

2 ( ) 10lg 1 ( ) N         ( ) 10lg 1 ( )c        2 ( ) 10lg 1 ( ) 10lg 2 3 c c c N  dB              滤波器的特性完全 由3dB截止频率 和阶数 N确定  滤波器的给定指标为  c  通带边界频率  p  阻带边界频率  通带最小幅度 | Ha ( j  ) |  s 1  通带最小幅度 2 1 2 1 1   1  阻带最大波纹  3dB截止频率与阶数如何确定 ？ 2 N = 8 N=4 N=2 1 A  3dB截止频率与阶数如何确定 ？ 13  c  N 8 0  c N

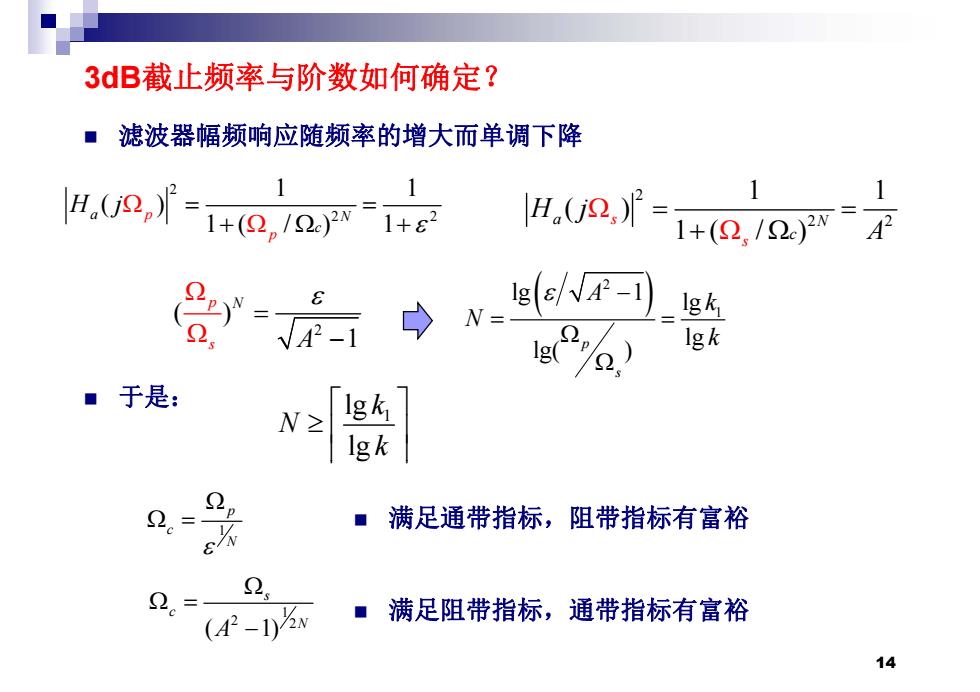
3dB截止频率与阶数如何确定？ ■滤波器幅频响应随频率的增大而单调下降 a,0o,f=10a H.U2,'= 1 +(2,122w= 后。 Igk Ig) Igk ■于是： Igk 1gk 22。 ■满足通带指标，阻带指标有富裕 2 2。- (A2-1)2w ■满足阻带指标，通带指标有富裕 14

3dB截止频率与阶数如何确定？  滤波器幅频响应随频率的增大而单调下降 2 2 2 1 1 ( ) 1( / ) 1 a p N c H j        2 2 2 1 1 ( ) 1( / ) H j a s N A    1( / ) 1   p c  1( / )    c   s A ( )  p N    2 1 lg 1 lg A k   2 ( ) 1 p N s A     1 lglg lg( ) p s k N k      于是： 1 lg lg k N k        g 1 p c N     满足通带指标，阻带指标有富裕  1  满足阻带指标，通带指标有富裕 s c    14 2 12  满足阻带指标，通带指标有富裕 ( 1) c N A 

<总结> ■滤波器的给定指标为 口通带、阻带边界频率 s 口通带最大衰减 ap=201g 1+8 口阻带最小衰减 a,=-201g()=201g A dB ■先求 8=V10“10-1 A=10,/20 ■ 确定阶数与截止频率 ge√R-可 lgk 2。= p Igk 2 2。= (A2-1)N 15

< 总结 >  滤波器的给定指标为  通带、阻带边界频率 1  p s  通带最大衰减 2 1 20 lg 1  p    1  阻带最小衰减 20lg( ) 20lg s A dB A     先求  确定阶数与截止频率 / 20 10 s A   /10 10 1  p     确定阶数与截止频率   2 1 lg 1 lg A k N   p     1 g lg lg( ) p s N k     c 1 N     s 15 1 2 2 ( 1) s c N A   

补充：模拟滤波器系统函数的求取H(2)→H(j2) ■定义振幅平方函数 A(Q2)=|H(j2)P=H.(j2)H.(j2)=H.(j)H(-j2) 口Ha(s)一模拟滤波器系统函数 ▣Ha(j2)一滤波器的频率响应 口|Ha(j2)|一滤波器的幅频响应 s=jn -52=22 A(-s2)=H(s)H.(-S)= 16

补充：模拟滤波器系统函数的求取 2 补充：模拟滤波器系统函数的求取 Hj Hj () ()    定义振幅平方函数 () () Hj Hj a a    定义振幅平方函数 2 2 A Hj Hj Hj Hj H j () () ()() ()( )             Ha(s)—模拟滤波器系统函数 () () ()() ()( ) A Hj Hj Hj Hj H j      a aa aa  Ha(s)—模拟滤波器系统函数  Ha(jΩ)—滤波器的频率响应  |Ha(jΩ)|—滤波器的幅频响应 2 2 2 1 ( ) () ( ) sj s A HH     2 2 1 ( ) () ( ) 1 a a N A s H s H s s j            16 c j     