
A(-s2)→H.(S) A(-s2)=H(s)H(-S) A(-S2)有2N个极点,且极点和零点总是“成对出现”,共轭对称;对称 于S平面的实轴和虚轴, ■选用A(-s2)的对称极、零点的任一半作为H(S)的极、零点,则 可得到H(s) 。 ■为了保证H(S)的稳定性,应选用A(-s)在$左半平面的极点作为 的极点H(S)。 ■零点的分布则无此限制,只和滤波器的相位特性有关, 口如果要求是最小相位延迟特性,则Ha(s)应取左半面零点, 口若无特殊要求,则可将对称零点的任一半(为共轭对)取为H,(S) 的零点。 17
2 As Hs ( ) () 2 A s H sH s ( ) () ( ) 有2N个极点,且极点和零点总是“成对出现”,共轭对称;对称 ( ) () As Hs a ( ) () ( ) A s H sH s a a 2 A s ( ) 有2N个极点,且极点和零点总是 成对出现 ,共轭对称;对称 于S平面的实轴和虚轴, 选用 的对称极 零点的任 半作为 的极 零点 则 A s ( ) 2 选用 A( ) 的对称极、零点的任一半作为 H ( ) 的极、零点,则 可得到 。 2 A( ) s ( ) H s a ( ) H a s 为了保证 的稳定性,应选用 在S左半平面的极点作为 的极点 。 ( ) H s a ( ) H s a 2 A( ) s 零点的分布则无此限制,只和滤波器的相位特性有关, 如果要求是最小相位延迟特性,则 Ha(s) 应取左半面零点 应取左半面零点, 若无特殊要求,则可将对称零点的任一半(为共轭对)取为 ( ) H s a 的零点。 17

H,(S)确定的方法如下: 1.由H(s)H(-s)0=|H(j2) 得到象限对称的s平面函数。 2.将H(2)进行因式分解,得到各零极点,将左半平面极点归 于H(S)。2轴上的零点或者极点都为偶次,应取一半(应为 共轭对)作为H(s)的零点或极点。 3.按照H(S)与H,(2)的低频或高频特性的对比就可以确定 出增益常数。 4. 由求出的零点,极点及增益常数,则可完全确定系统函数H(S)。 18
确定的方法如下: 1 由 得到象限对称的s平面函数 2 H (s)H ( s) H ( j) H (s) a 1. 由 得到象限对称的s平面函数。 2. 将 进行因式分解,得到各零极点,将左半平面极点归 ( ) ( ) ( ) H s H s H j a a s j a 2 H ( j) a 于 。 轴上的零点或者极点都为偶次,应取一半(应为 H (s) a j 共轭对)作为 的零点或极点。 3 按照 H ( ) 与 H ( j) 的低频或高频特性的对比就可以确定 H (s) a 3. 按照 与 的低频或高频特性的对比就可以确定 出增益常数。 H (s) a H ( j) a 4. 由求出的零点,极点及增益常数,则可完全确定系统函数 。 H (s) a 18

例:根据以下幅度平方函数H(2)确定系统函数H(s) HU=g+ 16(25-22)2 解: Step1: Hou(-以na.(a4ggt6 16(25+s2)2 Step2: 其极点为s=±7,±6,零点为s=±j5 H)=662+25) (s+7)(s+6) Step3: .Ha(s)=H(j)- .可以确定k。=4 H,(6)=42+25) 4s2+100 (s+7)(s+6)s2+13s+42 19
例 根据以下幅度平方函数 确定系统函数 2 例:根据以下幅度平方函数 H ( j) 确定系统函数 H (s) a H (s) a 16(25 ) ( ) 2 2 2 H j (49 )(36 ) ( ) 2 2 Ha j 解: 16(25 )2 2 (49 )(36 ) 16(25 ) ( ) ( ) ( ) 2 2 2 2 2 s s s H s H s H j a a s j a Step1: ( 25) s 7 6 s j5 2 k Step2: 其极点为 = , ,零点为 = ( 7)( 6) ( 25) H ( ) 2 0 a s s k s s ( ) ( ) 0 0 H s H j a s a 可以确定 Step3: 可以确定k0 4 4( 25) 4 100 H ( ) 2 2 s s 19 13 42 4 100 ( 7)( 6) 4( 25) H ( ) a 2 s s s s s s s

巴特沃斯低通滤波器的系统函数 |Ha(j2)2= 1+( ■将幅度平方函数转换成s域函数,(令S=2代入)有 Ha(S)Ha(-s)= 、1 1+( S ■令分母为零,得极点 Sk=(-1)2w(j2c)=2.em+) 式中,k=0,1,2,(2N一1) 20
巴特沃斯低通滤波器的系统函数 2 1 | ( )| H j a 2 1( ) a N c H j 将幅度平方函数转换成 s域函数,(令 代入)有 s j N a a s H s H s 2 1 ( ) 1 ( ) ( ) 令分母为零,得极点 N j c s 2 1 ( ) 1 2 1 2 2 1 ( ) 2 ( 1) ( ) k N j N k cc S je 式中, k = 0,1,2,(2N - 1 ) k cc 20
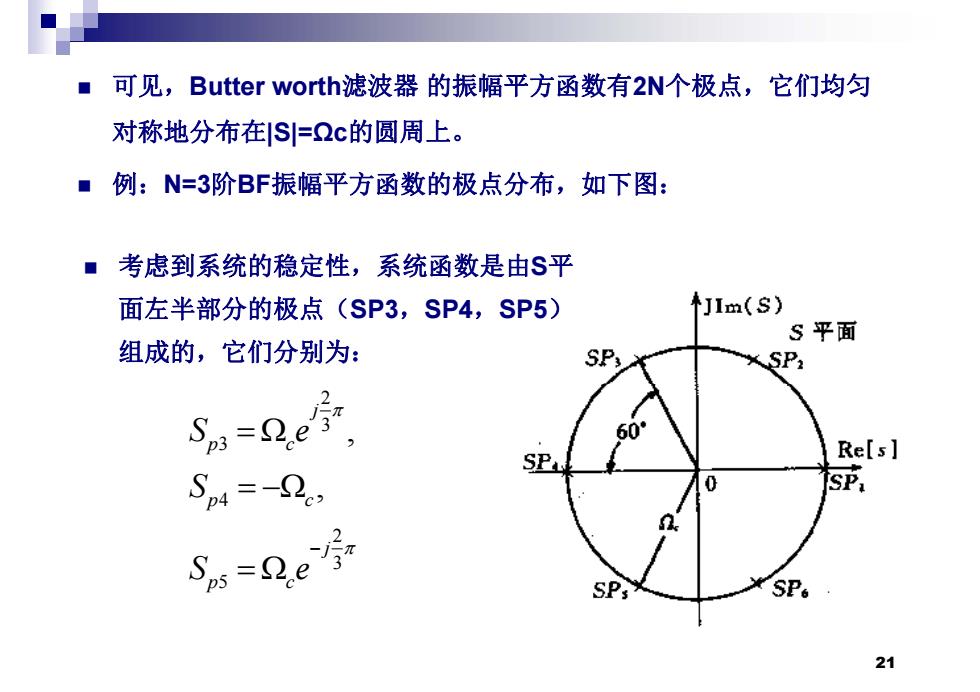
■ 可见,Butter worth:滤波器的振幅平方函数有2N个极点,它们均匀 对称地分布在S=c的圆周上。 ■例:N=3阶BF振幅平方函数的极点分布,如下图: ■考虑到系统的稳定性,系统函数是由$平 面左半部分的极点(SP3,SP4,SP5) 个JIm(s) S平面 组成的,它们分别为: SP3 X SP: =Qe'sT 60° Re[s] Sp4=-2., SP Sps=Qe SPs SPo 21
可见,B tt th Butter worth滤波器 的振幅平方函数有 的振幅平方函数有2N个极点,它们均匀 对称地分布在|S|=Ωc的圆周上。 例:N=3阶BF振幅平方函数的极点分布,如下图: 考虑到系统的稳定性,系统函数是由S平 面左半部分的极点 面左半部分的极点(SP3,SP4,SP5) 组成的,它们分别为: 2 3 3 , j p c S e 4 2 , p c S 3 5 j p c S e 21