
导 【思考辨析】 判断下列说法是否正确,正确的在后面的括号里画“V√”,错误 的画“X” (1)若二面角已定,点O在二面角棱1上的位置不同,则二面角的 平面角大小不同.(×) (2)若lLa,则经过的任何平面都与a垂直.(√) (3)若aLP,则B内任何直线都与a垂直.(×) (4)若平面a内有无数条直线与平面垂直,则a⊥.(√)
导航 【思考辨析】 判断下列说法是否正确,正确的在后面的括号里画“√”,错误 的画“×” . (1)若二面角已定,点O在二面角棱l上的位置不同,则二面角的 平面角大小不同.( ) (2)若l⊥α,则经过l的任何平面都与α垂直.( ) (3)若α⊥β,则β内任何直线都与α垂直.( ) (4)若平面α内有无数条直线与平面β垂直,则α⊥β.( ) × √ × √
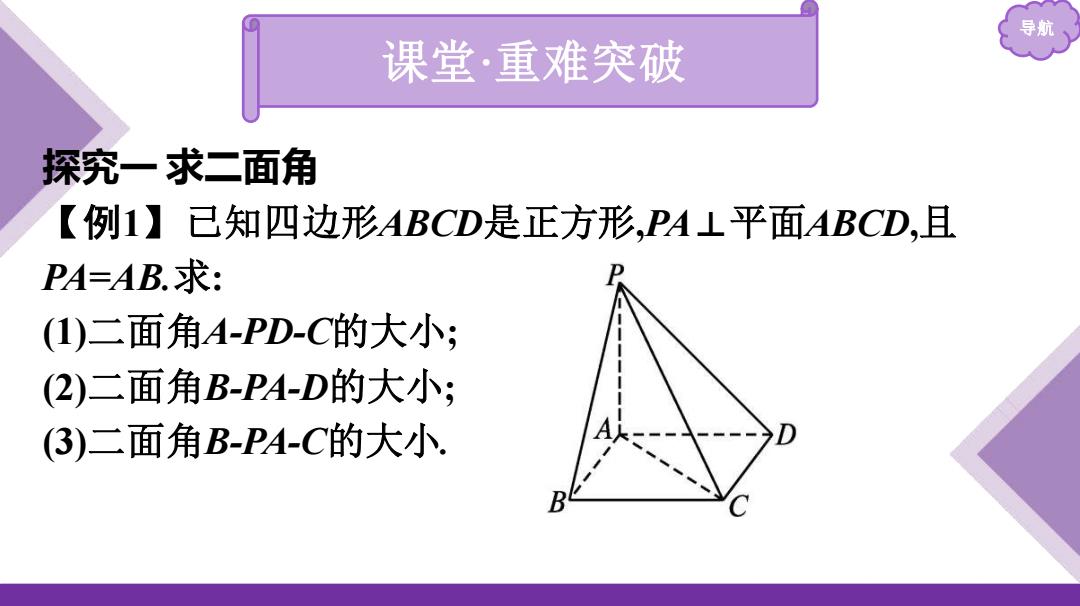
导航 课堂·重难突破 探究一求二面角 【例1】已知四边形ABCD是正方形,PAL平面ABCD,且 PA=AB.求: (1)二面角A-PD-C的大小; (2)二面角B-PA-D的大小; (3)二面角B-PA-C的大小. A人
导航 课堂·重难突破 探究一 求二面角 【例1】已知四边形ABCD是正方形,PA⊥平面ABCD,且 PA=AB.求: (1)二面角A-PD-C的大小; (2)二面角B-PA-D的大小; (3)二面角B-PA-C的大小

解:(1)PA⊥平面ABCD, 导航 PA⊥CD. 又四边形ABCD为正方形,'.CD⊥AD .PA∩AD=A,∴.CD⊥平面PAD,又CDC平面PCD, .‘.平面PAD⊥平面PCD .‘.二面角A-PD-C的大小为90°. (2).PA⊥平面ABCD,.∴AB⊥PA,AD⊥PA ∠BAD为二面角B-PA-D的平面角. 由题意可得∠BAD=90°, .二面角B-PA-D的大小为0°
导航 解:(1)∵PA⊥平面ABCD, ∴PA⊥CD. 又四边形ABCD为正方形,∴CD⊥AD. ∵PA∩AD=A,∴CD⊥平面PAD,又CD⊂平面PCD, ∴平面PAD⊥平面PCD. ∴二面角A-PD-C的大小为90° . (2)∵PA⊥平面ABCD,∴AB⊥PA,AD⊥PA. ∴∠BAD为二面角B-PA-D的平面角. 由题意可得∠BAD=90° , ∴二面角B-PA-D的大小为90°