北京化工大学：《机械创新》课程授课教案（课件讲稿）第六章 机构再生与创新设计

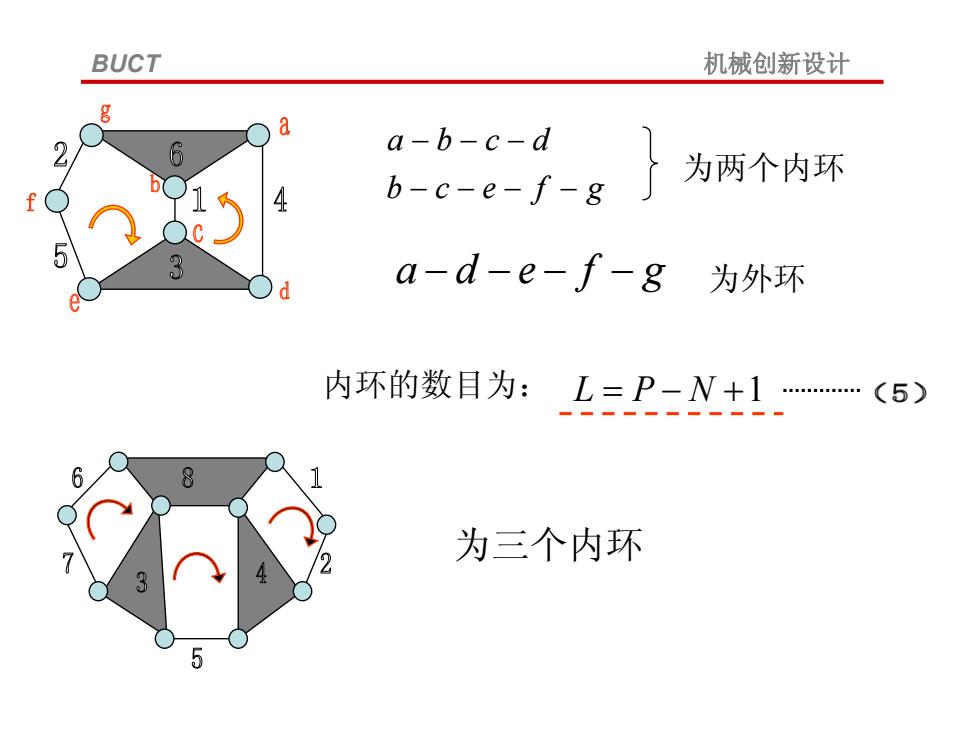
BUCT 机械创新设计 a-b-c-d b-c-e-f-8 为两个内环 a-d-e-f-g i 为外环 内环的数日为：L=P-N+1…(5) 8 为三个内环

gfecb dcba     为两个内环     gfeda 为外环 内环的数目为：   NPL 1 为三个内环 BUCT 机械创新设计

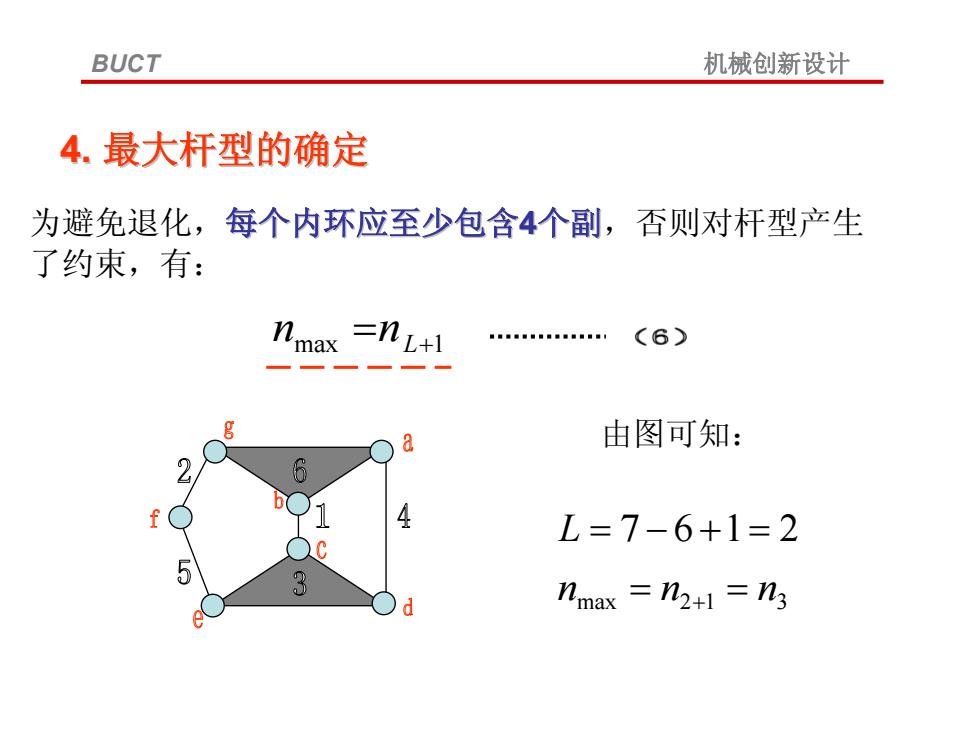
BUCT 机械创新设计 4.最大杆型的确定 为避免退化，每个内环应至少包含4个副，否则对杆型产生 了约束，有： nmax 二nL+1 ann1nn。■1 (6) g a 由图可知： 2 6 b(1 4 L=7-6+1=2 5 3 nmax =n2+1=n3

为避免退化，每个内环应至少包含 每个内环应至少包含4个副，否则对杆型产生 了约束，有： max  L1 nn 由图可知： max 312 2167 nnn L       4. 最大杆型的确定 最大杆型的确定 BUCT 机械创新设计

BUCT 机械创新设计 8 3 由图可知： 5 L=10-8+1=3 nmax =n3+l=n4

由图可知： 413max 31810 nnn L       BUCT 机械创新设计

BUCT 机械创新设计 六杆七副运动链的杆型类配方案 由(3)式可知有2个三副杆，由(4)式可知有4个二副杆 3 (2)式-2×(1)式 得：n3+2n4+…(n-2)nn=2(P-N)(3) n2=N-n3-n4-…-nm

由（3）式可知有2个三副杆，由（ 个三副杆，由（4）式可知有4个二副杆 六杆七副运动链的杆型类配方案 六杆七副运动链的杆型类配方案 BUCT 机械创新设计 )(2)2(2 )1(2)2( 3 4 n  NPnnnn  得：  式 式 2    43    nnnNn n

BUCT 机械创新设计 八杆十副运动链的杆型类配方案 L=10-8+1=3 nmax =n3+1-n4 按(3)， (4)式进行类配得下表： 类配方案 n2 na n4 I 4 4 0 Ⅱ 5 2 1 瓜 6 0 2 (2)式-2×(1)式 得： n3+2n4+…(n-2)nm=2(P-N)(3) n2=N-n3-n4-…-nm …(4)

八杆十副运动链的杆型类配方案 八杆十副运动链的杆型类配方案 类配方案 n 2 n 3 n 4 Ⅰ 4 4 0 Ⅱ 5 2 1 Ⅲ 6 0 2 413max 31810 nnn L       按（ 3），（ 4）式进行类配得下表： BUCT 机械创新设计 )(2)2(2 )1(2)2( 3 4 n  NPnnnn  得：  式 式 2    43    nnnNn n