西安电子科技大学：《数字信号处理》课程教学课件（讲稿）07 FIR数字滤波器（FIRDF）设计

2.2频域约束（对H(ω)的约束) ■两类线性相位FIR滤波器在N取奇数和偶数时，幅度特性 各不相同。 ■两个参数： W-1 T= 2 (1)情况1：h(n)=h(N-n-1),N为奇数 (2)情况2：h(n)=h(N-n-1),N为偶数 (3)情况3：h(n)=h(N-n-1),N为奇数 (4)情况4：h(n)=-h(N-n-1),N为偶数 22

2.2 频域约束（ 对Hg 2.2 频域约束（ 对Hg(ω)的约束 ）  两类线性相位FIR滤波器在N取奇数和偶数时，幅度特性 各不相同。 两个参数 N 1 N 1 M       两个参数： 2   2 M        （1）情况1：h(n)=h(N-n-1)，N为奇数 （2）情况2：h(n)=h(N-n-1)，N为偶数 （3）情况3：h( ) n =-h(N-n-1)，N为奇数 （4）情况4：h(n)=-h(N-n-1)，N为偶数 22

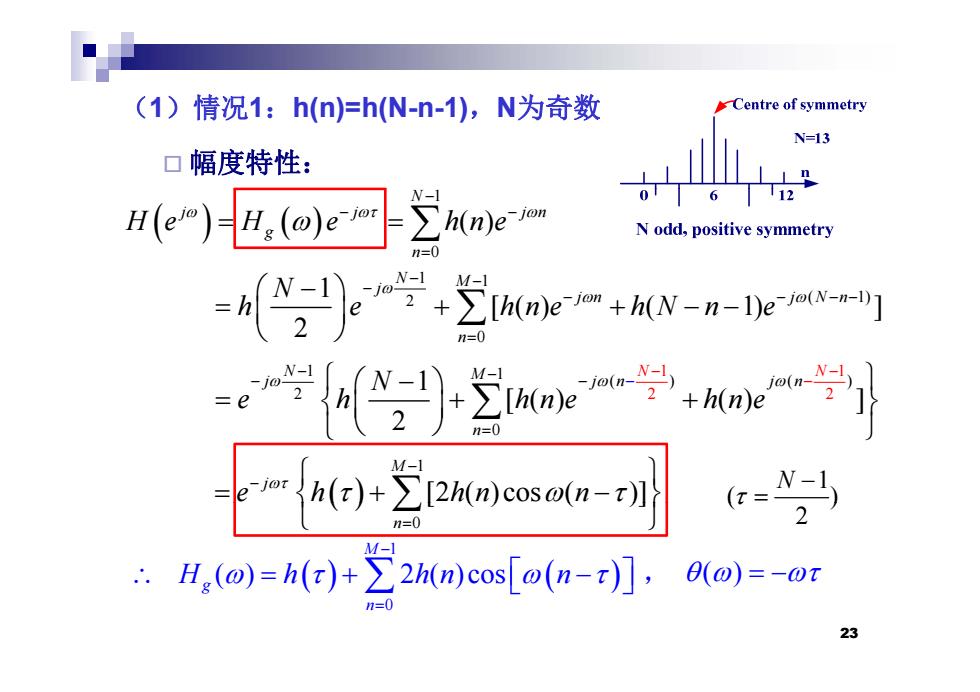
(1)情况1：h(n)=h(N-n-1),N为奇数 Centre of symmetry N=13 口幅度特性： N- 6112 H(e）uo)e h(n)e-jon N odd,positive symmetry M-1 n=0 )+(-) n=0 ∴.H(o)=h(x)+∑2hn)cos[o(n-t)],8(o)=-or 23

（1）情况1：h(n)=h(N h(n)=h(N-n-1)，N为奇数  幅度特性：     1 0 ( ) N j j jn g n H e H e hne            1 1 2 ( 1) 0 1 [ ( ) ( 1) ] 2 N M j jn j Nn n N h e hne hN n e                       1 1 () ( 1 ) 2 2 1 2 0 1 [() () ] 2 N M j j N n N N j n e h hne hne                              2 n0   1 [2 ( ) cos ( )] M j e h hn n                1 ( ) N        1 ( ) 2 ( )cos M H h hn n              ，    ( )     0 [ ( ) ( )] n      ( ) 2  23     0 ( ) 2 ( )cos g n H h hn n            ，    ( )

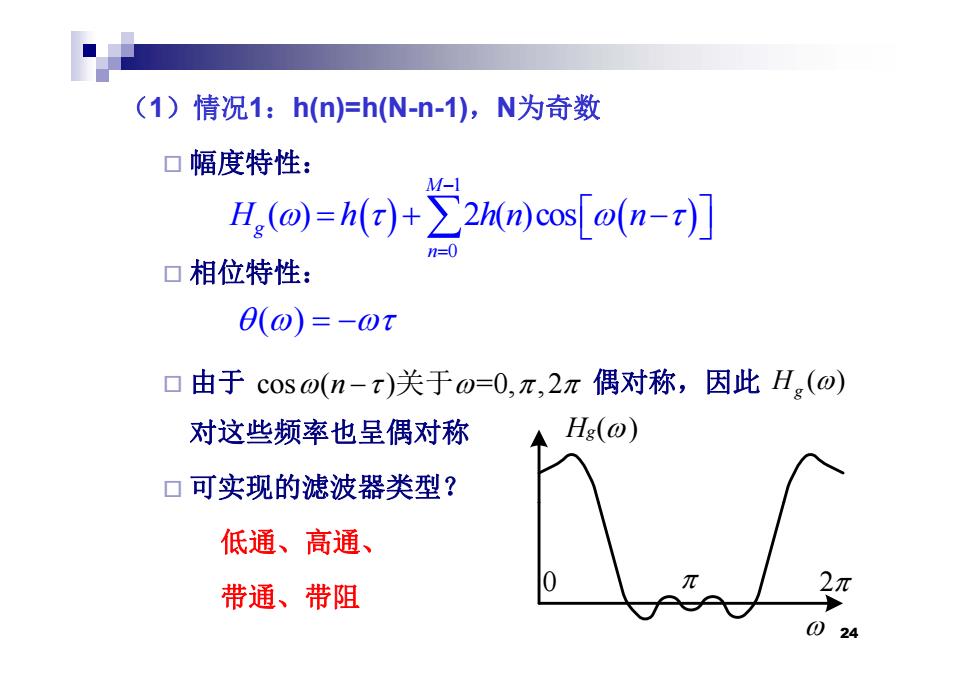
(1)情况1：h(n)=h(N-n-1),N为奇数 口幅度特性： M- H,(o=h()+∑2 h()cos[o(n-z】 口相位特性： 0(0)=-0x 口由于coso(n-x)关于o=0,π，2π偶对称，因此H.(o) 对这些频率也呈偶对称 、Hg(o) 口可实现的滤波器类型？ 低通、高通、 带通、带阻 2元 024

（1）情况1：h(n)=h(N h(n)=h(N-n-1)，N为奇数  幅度特性： M1  相位特性     1 0 ( ) 2 ( )cos M g n H h hn n             相位特性：  ( )      由于 偶对称，因此 对这些频率也呈偶对称 H () cos ( ) =0, ,2  n    关于 ( ) Hg  对这些频率也呈偶对称  可实现的滤波器类型？ Hg() 低通、高通、 0  2 24 带通、带阻 0  2 

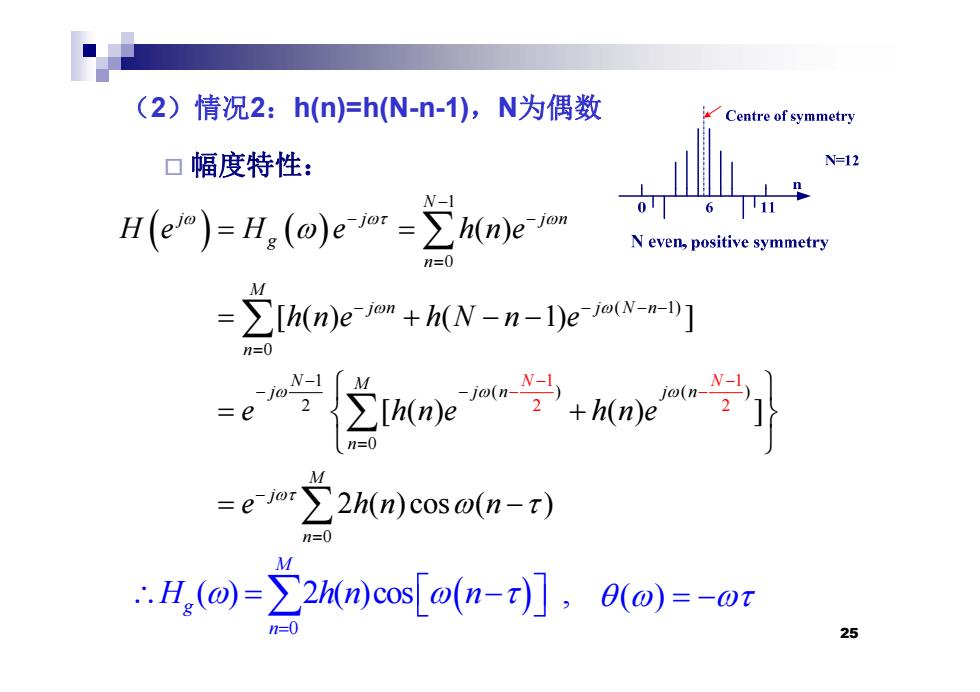
(2)情况2：h(n)=hN-n-1),N为偶数 Centre of symmetry 口幅度特性： N=12 H(eP）=H,(o)eim-∑mem N-1 T 6. N even,positive symmetry n=0 =之hmee侧+hN-n-lea-n] n=0 e M =er22hm)cosw(n-） n=0 ∴.Hg(o)=∑2ncos[o(n-t]，6o)=-or 25

（2）情况2：h(n)=h(N h(n)=h(N-n-1)，N为偶数  幅度特性：     1 0 ( ) N j j jn g n H e H e hne            ( 1) 0 [ ( ) ( 1) ] M jn j Nn hne hN n e          1 0 1 ( ) 1 ( ) 2 2 2 [() () ] n N M j jn jn N N e hne hne                   0 [() () ] 2 ( )cos ( ) n M j e hn n             0 2 ( )cos ( ) j n e hn n       ( ) 2()   M  h   25   0 ( ) 2()cos , g n H  h n n             ( )    

(2)情况2：h(n)=h(N-n-1),N为偶数 口幅度特性： H.(@)=>2h(n)cos[o(n-t)] n=0 口相位特性： 0(o)=-0x 口由于coso(n-)关于o=0,2π偶对称，因此H.(o) 对这些频率也呈偶对称。 口由于cos[π(n-t)]=cosπn-N/2+1/2】=-sinlπn-N/2]=0 ∴.H.(π)=0 且coso(n-T)关于o=π奇对称，故H.(o)也呈奇对称。 口可实现的滤波器类型？ 不能用于设计高通、带阻滤波器。(H(π)=O) 26

（2）情况2：h(n)=h(N h(n)=h(N-n-1)，N为偶数  幅度特性： ( ) 2 ( )cos   M H hn n g          相位特性：  ( )       0 ( ) () g n     由于 偶对称，因此 对这些频率也呈偶对称 cos ( ) =0,2  n   关于 ( ) Hg  对这些频率也呈偶对称。  由于 cos cos[ ( / 2 1/ 2)] sin[ ( / 2)] 0      n nN nN           奇对称 故 也 奇对称 () 0  Hg   且 关于 奇对称，故 也呈奇对称。  可实现的滤波器类型？ cos ( ) =  n   关于 ( ) Hg  不能用于设计高通、带阻滤波器。 26 ( ( ) 0) Hg  