西安电子科技大学：《数字信号处理》课程教学课件（讲稿）07 FIR数字滤波器（FIRDF）设计

(3)情况3：h(n)=-h(N-n-1),N为奇数 Centre of symmetry N=7 口相位特性：0(0)=-π/2-0t 16 N odd,negative symmetry 口幅度特性： H)=H.()h()=0 N-I h(n)e+h(-n-1)em- M- =∑h(n)eow-h(n）eaw-] 27

（3）情况3：h(n)=-h(N-n-1)，N为奇数  相位特性：  ( )       / 2  幅度特性： ( )      1 ( ) 0 N j j jn g n He H e hne           1 ( )0 2 N h   n 0      1 1 1 M j n j Nn hne hN n e              n0       1 1 M j j N         1 0 [ ] j n j N n n hne hne          27

(3)情况3：h(n)=-h(N-n-1),N为奇数 H(e)-Ih(r)e-h(n)e =e览me学-Me学】 n=0 -e空24(oma-》 =0 3y2a(间sm[ow-月-H.@jea e .H.(@)=>2h(n)sin[o(n-t)] 28

（3）情况3：h(n)=-h(N-n-1)，N为奇数         1 1 [ ] M j jn j Nn He hne hne           （3）情况3：h(n) h(N n 1)，N为奇数       0 1 1 () () 1 1 [ ] n j N M jn jn N N He hne hne                     () () 2 0 2 2 [() () ] j jn jn n e hne hne               1 1 2 0 1 2 sin 2 j N M n N je h n n                                  0 1 2 ( ) 2 sin n j M j e hn n H e                                  0 2 sin g n e hn n H e             M 1    28     0 ( ) 2 sin g n H hn n            

(3)情况3：h(n)=-h(N-n-1),N为奇数 口相位特性： 0(o)=-π/2-0x M-1 口幅度特性： H.(@)=>2h(n)sin[o(n-)] 口sin[o(n-t)]关于o=0,π，2π点呈奇对称，故H.(o)对 这些点也呈奇对称 口o=0,π，2π时，sinn0=0,H.(o)=0,即Hz)在z=±1 处有两个零点 口可实现的滤波器类型？ 不能设计H(O)≠0和H(π)≠0的滤波器，故不能实现 低通、高通和带阻滤波器，只能实现带通滤波器。29

（3）情况3：h(n)=-h(N-n-1)，N为奇数  相位特性： （3）情况3：h(n) h(N n 1)，N为奇数  ( ) /2        幅度特性：    1 0 ( ) 2 sin M g n H hn n              点呈奇对称，故 对 这些点也呈奇对称 n 0 ( ) sin[ ( )] =0, 2  n    关于 ， Hg  这些点也呈奇对称    =0, ,2 时，sin n   0, ( ) 0, Hg  即H(z)在 z  1 处有两个零点   0, ,2 s 0, ( ) 0, g n  z 1  可实现的滤波器类型？ 不能设计 H H (0) 0 ( ) 0   和  的滤波器，故不能实现 低通、高通和带阻滤波器，只能实现带通滤波器。 29 H H (0) 0 ( ) 0   和 

(4)情况4：h(n)=-h(N-n-1),N为偶数 Centre of symmetry N=8 ▣相位特性：（⊙）=-π/2-oz x=N/2-1/2 N even,negative symmetry 口幅度特性：H,(o)=∑2h(n)sin[o(n-t)] n=0 口H,(o)在0=0,2π处为零，即H(z)在z=1处有零点 口H(0)关于o=0,2π奇对称，关于0=π偶对称 口可实现的滤波器类型？ 不能用于设计低通和带阻滤波器 (H(0)=0) (H(2π)=0) 30

（4）情况4：h(n)=-h(N-n-1)，N为偶数  相位特性：  ( ) /2         N /2 1/2  M  幅度特性：     0 ( ) 2 sin M g n H hn n             Hg ( )  在 处为零，即 =0,2 H(z)在 z=1处有零点  关于 奇对称，关于 偶对称 可实现的滤波器类型？ ( ) Hg  =0, 2 =  可实现的滤波器类型？ 不能用于设计低通和带阻滤波器 ( (0) 0) Hg  30 ( (2 ) 0) Hg  

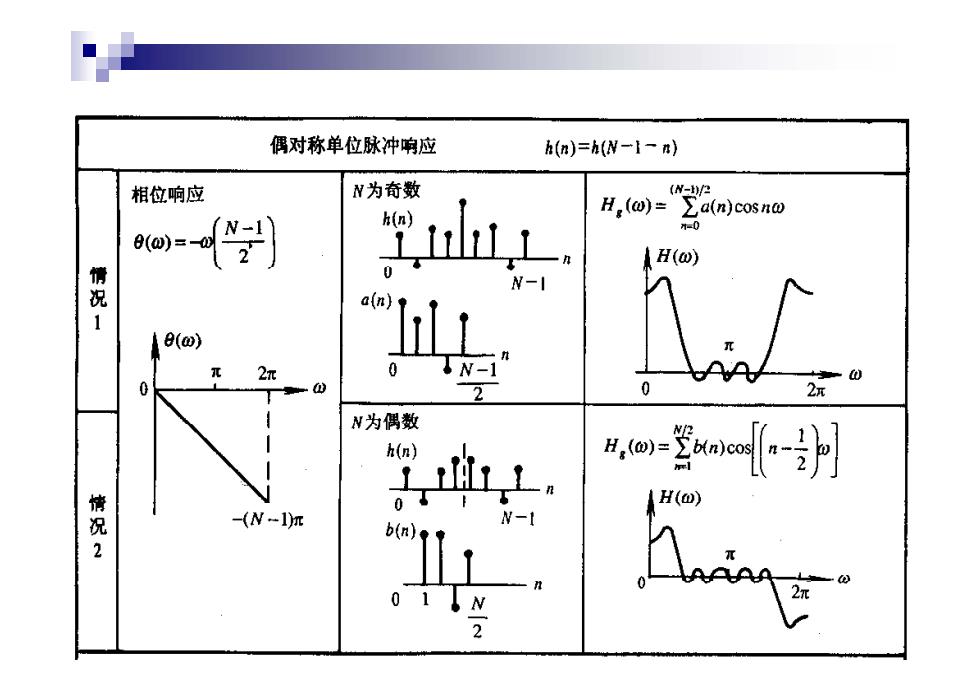
偶对称单位脉冲响应 h()=(N-i一) 相位响应 N为奇数 (w-/2 h(n) H,(@)=∑a(n)cOSn@ -0 ()= H(ω) 情 N-I a(n)◆ 1 (@) 2π 0N-i” 0 2 N为偶数 h(n) 侧-a-】 情 H() -(N-1)π W-1 2 01N

31