西安电子科技大学：《数字信号处理》课程教学课件（讲稿）07 FIR数字滤波器（FIRDF）设计

■第二类线性相位 0(0)=-π/2-0x W-1 H(e)=>h(n)e ion =H()e) n=0 W >h(n)(cos@n-jsin@n)=-Hg(@)(sin@t+jcos@7) n=0 W-1 -H,(o)sinor=∑h(m）coswn n=0 N-1 Hg(@)cosor=>h(n)sinon n=0 17

 第二类线性相位     ( ) /2 1 ( /2 ) N j jj       ( ) /2    ( /2 ) 0 ( ) () ( ) j j n j g n H e hne H e             N1 0 ( )(cos sin ) ( )(sin cos ) g n hn n j n H j           1 0 ( )sin ( )cos N H g    hn n     0 1 ( )cos ( )sin n N H hn n        0 ( )cos ( )sin g n H hn n      17

W N -H(@)sinot= ∑A(n)）coswn H(@)cosor= ∑m)sin@n n=0 n=0 N-1 h(n)coson sin @t n=0 cos@t N ∑h(n))sin wn n=0 N-1 N-1 cos@r∑h(n)）cos @n+-sin@r∑h(n)sin on=0 n=0 n=0 ■三角函数的恒等关系 艺h0 m)coso(n-t)=0 n=0 18

N N   1 1   0 0 ( )sin ( )cos ( )cos ( )sin g g n n H       hn n H hn n       1 ( ) N h  0 1 ( ) cos sin cos n N h n n         0 cos ( )sin n hn n     1 1 0 0 cos ( )cos sin ( )sin 0 N N n n     hn n hn n        三角函数的恒等关系 n n 0 0 1 ( )cos ( ) 0 N hn n       18 n  0

N-1 h(n)coso(n-t)=0 n=0 ■满足上式的一组解 口h(n)coso(n-t)关于求和区间的中心(N-1)/2奇对称 ■因为coso(n-x)关于n=t偶对称，令t=(N-1)/2 则要求h(n)关于(N-1)/2奇对称 即 -or,=(N-1) 2 h(n)=-h(W-1-n)0≤n≤W-1 19

1 ( )cos ( ) 0 N hn n     满足上式的 组解 0 ( )cos ( ) 0 n hn n        满足上式的一组解  hn n ( )cos ( )   关于求和区间的中心 奇对称 (N 1)/2  因为 关于 偶对称，令 cos ( ) (N 1) / 2  n n=     ( ) 则要求 关于 奇对称 即： h(n) ( 1)/2 N   1 即 ( ) , ( 1) 2 2 N           hn hN n n N () ( 1 ) 0 1       19

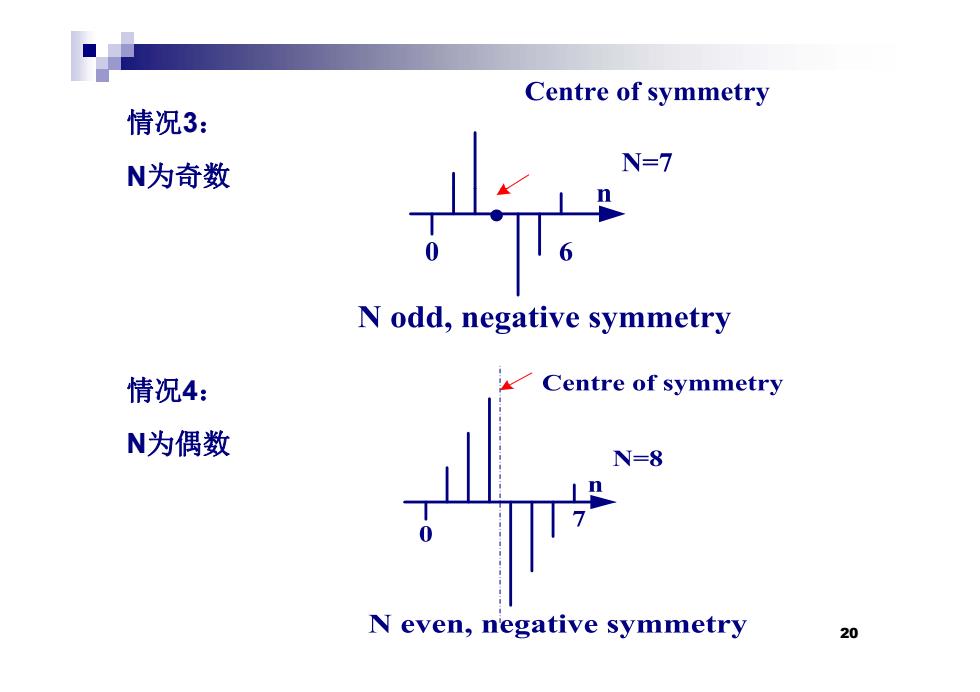
Centre of symmetry 情况3： N为奇数 N=7 N odd,negative symmetry 情况4： Centre of symmetry N为偶数 N=8 N even,negative symmetry 20

情况3： N为奇数 情况4： N为偶数 20

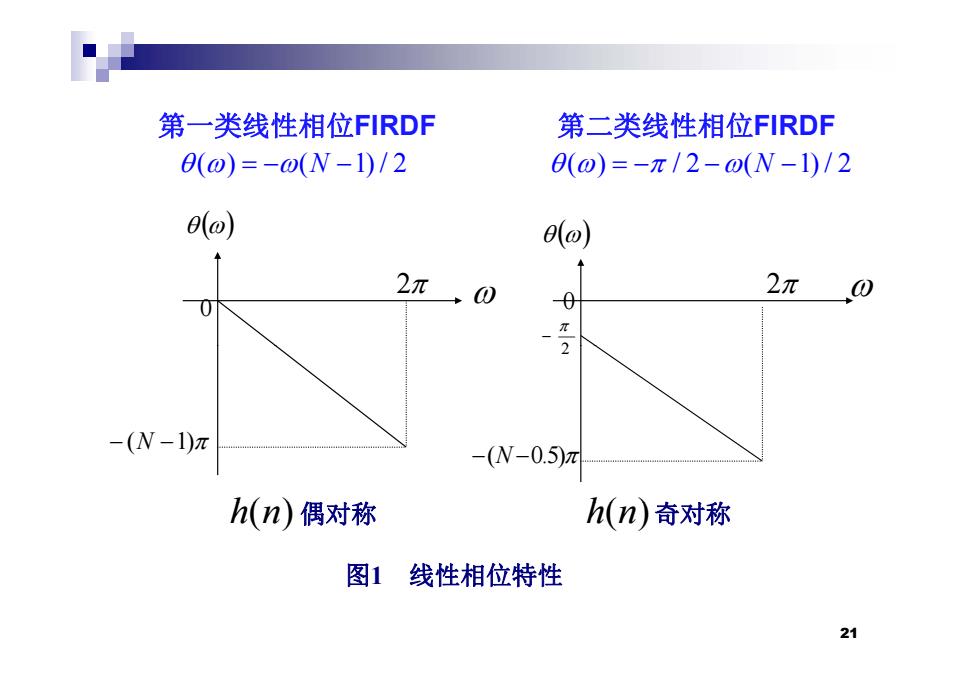
第一类线性相位FIRDF 第二类线性相位FIRDF 0(o)=-o(N-1)/2 θ(o)=-π/2-o(N-1)/2 eld) ea) 2π 0 2π 0 0 -(N-1)π -(N-0.5)m h(n)偶对称 h(n)奇对称 图1 线性相位特性 21

第一类线性相位FIRDF 第二类线性相位FIRDF  ( ) ( 1) / 2     N  ( ) / 2 ( 1) / 2      N      2  0 2  0 2    (N 1) (N0.5) h(n) 偶对称 h(n) 奇对称 图1 线性相位特性 21