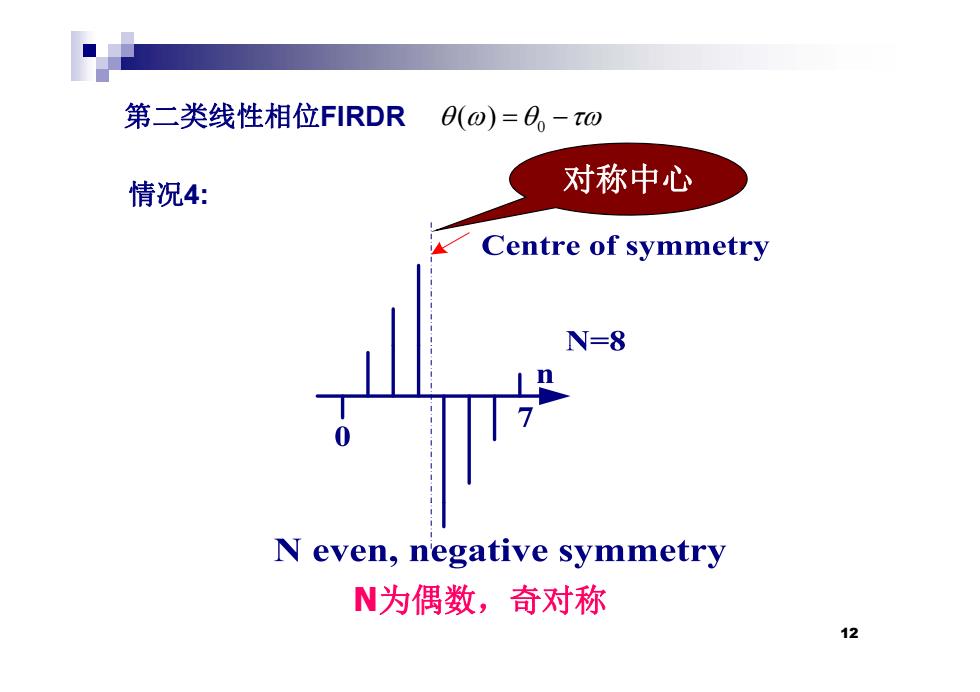
第二类线性相位FIRDR(o)=O。-t0 情况4: 对称中心 Centre of symmetry N=8 N even,negative symmetry N为偶数,奇对称 12
第二类线性相位FIRDR ( ) 情况4 对称中心 第二类线性相位FIRDR 0 ( ) 情况4: 对称中心 12 N为偶数,奇对称

2.线性相位条件对FIRDF时域和频域的约束 2.1时域约束(对h(n)的约束) ■第一类线性相位:O(0)=-T0 H(h(n)e-H()-H(O)e W-1 n=0 Xcoson-faimnon)-H.(aXcoxr-jsinot) n=0 N-l H(@)cos@T=>h(n)coson n=0 N-1 Hg(@)sinor=>h(n)sin on 13 m=0
2. 线性相位条件对FIRDF时域和频域的约束 2.1 时域约束( 对h( ) n 的约束 ) 第一类线性相位: N 1 () 1 ( ) 0 ( ) () ( ) ( ) N j jn j g n j He hne H Hg e e n 0 1 ( )(cos sin ) ( )(cos sin ) N g hn n j n H j 0 g n 1 ( )cos ( )cos N H hn n 0 1 ( )cos ( )cos g n N H hn n 13 0 ( )sin ( )sin g n H hn n

H.(@)cosor-)cosom H.(o)sinor=】 之)sin oz n=0 n=0 acosom coswt n=0 sin@t N-1 h(n)sin on n=0 N-1 N-1 sinor∑h(n)coson=coS@T∑h(n)sin on n=0 n=0 ■三角函数的恒等关系 N-1 h(n)sino(n-t)=0 n=0 14
N N 1 1 0 0 ( )cos ( )cos ( )sin ( )sin g g n n H hn n H hn n 1 ( )cos cos N hn n 0 1 cos sin ( )sin n N hn n 0 ( ) n N N 1 1 0 0 sin ( )cos cos ( )sin n n hn n hn n 三角函数的恒等关系 1 ()i ( ) 0 N h 14 0 ( ) s i n ( )0 n h n n

N-1 h(n)sino(n-t)=0 n=0 ■满足上式的一组解 口h(n)sino(n-t)关于求和区间的中心(N-1)/2奇对称 ■因为sino(n-x)关于n=x奇对称,令x=(N-1)/2 则要求h(n)关于(N-1)/2偶对称 即: h(n)=h(W-1-n0≤n≤N-1 (0)=-0x C-p-w 15
1 ( )sin ( ) 0 N hn n 满足上式的一组解 0 ( )sin ( ) 0 n hn n 满足上式的一组解 hn n ( )sin ( ) 关于求和区间的中心 奇对称 ( 1)/2 N 则要求 关于 偶对称 因为 关于 奇对称,令 sin ( ) (N 1) / 2 n n= 则要求 h( ) 关于 ( 1)/2 N 偶对称 即: h(n) ( 1)/2 N () ( 1 ) 0 1 ( ) hn hN n n N ( ) 1 1 ( ) ( 1) ( 1) 2 N N 15 ( 1) 2 2 N
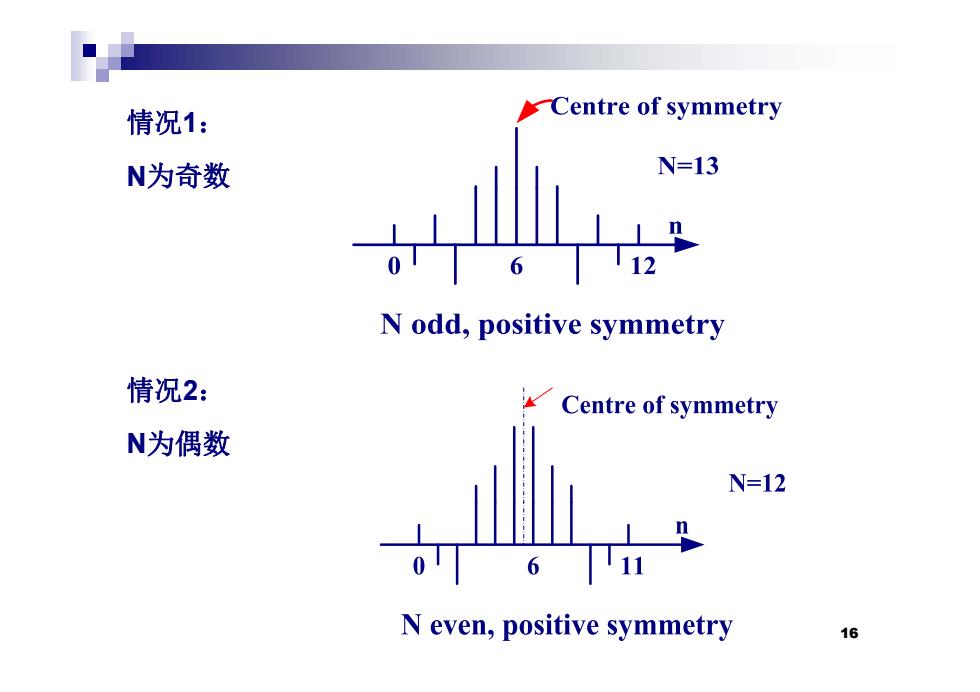
情况1: Centre of symmetry N为奇数 N=13 T12 N odd,positive symmetry 情况2: Centre of symmetry N为偶数 N=12 6 N even,positive symmetry 16
情况1: N为奇数 情况2: N为偶数 16