西安电子科技大学：《数字信号处理》课程教学课件（讲稿）07 FIR数字滤波器（FIRDF）设计

1.FIR滤波器的定义 ■传输函数 N-I He)=-∑hln)e=H(o)eo, n=0 口幅度特性（可为负值）Hg(0) 与幅频响应不同 口相位特性 θ(0) .与相频响应不同 ■第一类线性相位FIRDR 口严格线性函数： 0(0)=-t0 ■第二类线性相位FIRDR 口满足： 0(0)=8,-t0 π T为常数，日，为起始相位 80= 2

1．FIR滤波器的定义  传输函数 1 ( ) ( ) () ( ) N j jn j He hne H e           幅度特性（可为负值） 0 ( ) () ( ) g n He hne H e       幅度特性（可为负值） Hg() - 与幅频响应不同  相位特性 Hg()  () 与幅频响应不同 - 与相频响应不同  第一类线性相位FIRDR  严格线性函数：  ()    第二类线性相位FIRDR  ()     ( )  满足： 为常数 为起始相位 0  ( )           7  为常数， 0 为起始相位 0 2   

系统的群时延 t(o)- dθ(o) do 群时延均为常数，称为恒定群延时滤波器： d0(o) do (θ(o)=-t0,0(o)=0,-t0)

系统的群时延 ( ) ( ) d d      群时延均为常数，称为恒定群延时滤波器 恒定群延时滤波器： d ( ) d     （， ）  ()   0  ( )      8

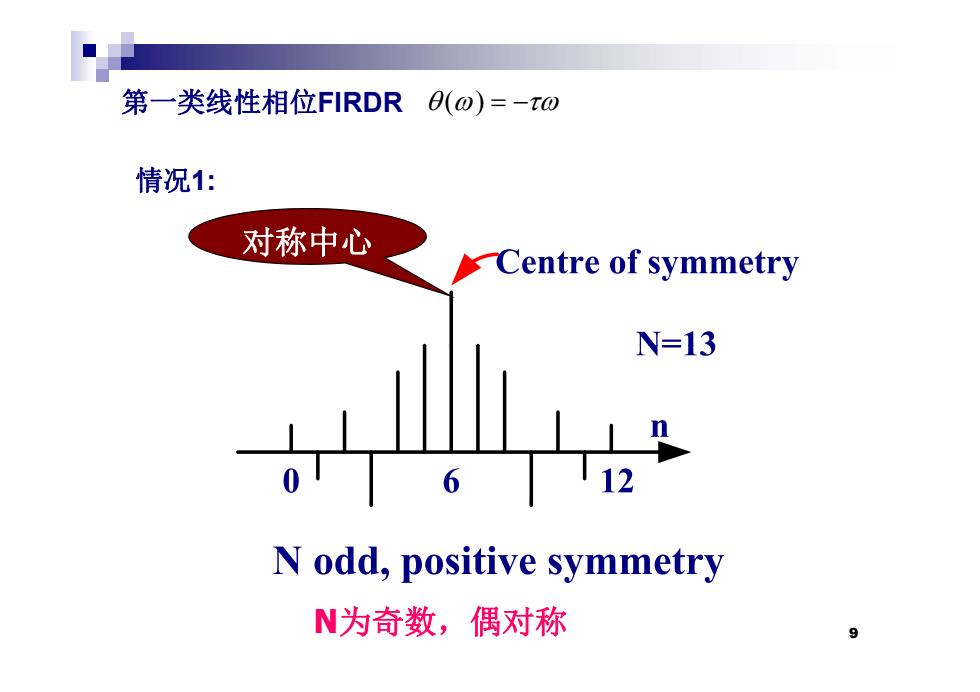
第一类线性相位FIRDR(o)=-tO 情况1： 对称中心 Centre of symmetry N=13 N odd,positive symmetry N为奇数，偶对称

第 类线性相位 一 FIRDR  ()   情况1:  ()  情况1: 对称中心 N为奇数，偶对称 9

第一类线性相位FIRDR(o)=-to 情况2： 对称中心 Centre of symmetry N=12 n N even,positive symmetry N为偶数，偶对称 10

第一类线性相位FIRDR  ()   情况 2: 对称中心 第 类线性相位FIRDR  ()  情况 2: 对称中心 10 N为偶数，偶对称

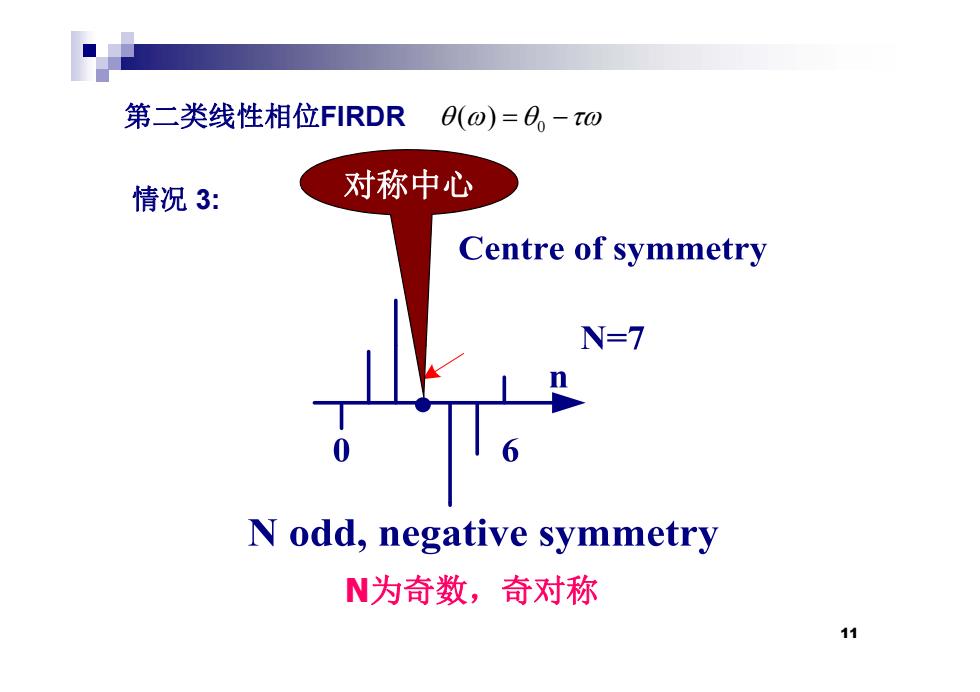
第二类线性相位FIRDR 0(0)=0-t0 情况3： 对称中心 Centre of symmetry N=7 N odd,negative symmetry N为奇数，奇对称 11

第二类线性相位FIRDR   ( ) 情况 3 对称中心 第二类线性相位FIRDR 0  ( )     情况 3: 对称中心 N为奇数 奇对称 11