
课程目标3:掌握微分中值定理的内容与证明。会用中值定理证明一些恒等式、不等式。 熟练地应用洛必达法则求不定式的极限。掌握常见函数的泰勒展式。 课程目标4:理解原函数与不定积分的概念。熟记基本积分公式表。熟练掌握换元积分 法与分部积分法。了解有理函数和三角有理式,并会利用它来求简单函数的积分。会计算简 单无理函数的积分。 课程目标5:理解定积分的概念。掌握可积的充分条件,并能应用它判断一些函数的可 积性(包括可积函数类)。熟练掌握定积分性质与积分上限函数的性质。能熟练地应用牛顿 一一莱布尼兹公式,换元积分法与分部积分法计算一些定积分。掌握用定积分表达一些几何 量与物理量的方法。会计算反常积分。 课程目标6:理解函数极值概念,会利用导数讨论函数的单调性、凹凸性,会求函数的 极值与最值和凹凸区间与拐点。能应用导数较正确地作出函数图象。会求函数图像的弧长和 曲率,理解并学会利用弧微分。 课程目标7:用微积分的发展历史激励学生的民族自豪感和责任感:数学发展的三次危 机的解决让学生懂得危机与机遇并存,只要坚定科学的理念、正确的方法,就会迎来更大的 发展。 课程目标8:通过数学强大的严谨性和逻组性,逐步培养学生一丝不荀、实事求是的科 学态度。通过数学解题的探求,使学生体验到挫折和失败,磨练学生的心理品质,使学生形 成不怕困难、刻苦钻研的优秀品格。通过培养学生的数学意识和应用数学的能力,逐步培养 学生理论联系实际的作风。 课程目标与毕业要求的关系矩阵 毕业要求的知识和能力 能力6 能力7 能力8 能力11 课程目标】 课程目标2 课程目标3 课程目标4 课程目标5 课程目标6 二、教学内容 理论教学安排
21 课程目标 3:掌握微分中值定理的内容与证明。会用中值定理证明一些恒等式、不等式。 熟练地应用洛必达法则求不定式的极限。掌握常见函数的泰勒展式。 课程目标 4:理解原函数与不定积分的概念。熟记基本积分公式表。熟练掌握换元积分 法与分部积分法。了解有理函数和三角有理式,并会利用它来求简单函数的积分。会计算简 单无理函数的积分。 课程目标 5:理解定积分的概念。掌握可积的充分条件,并能应用它判断一些函数的可 积性(包括可积函数类)。熟练掌握定积分性质与积分上限函数的性质。能熟练地应用牛顿 ——莱布尼兹公式,换元积分法与分部积分法计算一些定积分。掌握用定积分表达一些几何 量与物理量的方法。会计算反常积分。 课程目标 6:理解函数极值概念,会利用导数讨论函数的单调性、凹凸性,会求函数的 极值与最值和凹凸区间与拐点。能应用导数较正确地作出函数图象。会求函数图像的弧长和 曲率,理解并学会利用弧微分。 课程目标 7:用微积分的发展历史激励学生的民族自豪感和责任感;数学发展的三次危 机的解决让学生懂得危机与机遇并存,只要坚定科学的理念、正确的方法,就会迎来更大的 发展。 课程目标 8:通过数学强大的严谨性和逻辑性,逐步培养学生一丝不苟、实事求是的科 学态度。通过数学解题的探求,使学生体验到挫折和失败,磨练学生的心理品质,使学生形 成不怕困难、刻苦钻研的优秀品格。通过培养学生的数学意识和应用数学的能力,逐步培养 学生理论联系实际的作风。 课程目标与毕业要求的关系矩阵 毕业要求的知识和能力 能力6 能力7 能力8 能力11 课程目标1 √ √ √ √ 课程目标2 √ √ √ √ 课程目标3 √ √ √ √ 课程目标4 √ √ √ √ 课程目标5 √ √ √ √ 课程目标6 √ √ √ √ 二、教学内容 理论教学安排
教学内容 学时 备注 支排课程目标 3456 78 九个常用的念初等 连续 30 的 限极限的 小与无穷大,无 20 作业:相应 四章微分中值定理 12 作业:相 微分中值定理洛必达法则泰勒公 五意不积分执元积分法分 10 作 部积分法几类函数的积分 习若干 分敛散性判 习题若干 F 导数 10 分析作图 曲线的: 习题若干 在经济学中的应用 微积分 三、教学方法 针对《数学分析》课程的特点,除使用系统讲授法、自学指导法、习题课等常规的教学 方法外,对部分内容也可尝试使用一些国内外专家结合生理学、心理学的新成就而创造的新 型的教学方法,如发现教学法、问题教学法、学导式教学法等。 1、突出学生的主体地位,改进教学方法 数学教学不应是以教师为主的知识传授过程,而应该是以学生为主的发现过程(再发现 过程),应该让学生主动去进行探索、猜测、修正等活动。让学生通过解决问题的过程去学 习数学,去认识数学,学会“数学地”思维,并逐步树立起对自身数学能力的信心,最终提 高学生解决问题的能力。而教师则以示范者、咨询者、启发者、鼓励者和质疑者来体现“教 学过程”活动中的主导作用。 教学中注意引导学生体会教学概念、原理中的丰富思想,学习其表达与处理问题的方法。 力戒将定型教条强灌给学生,不论其消化与香就通迫学生陷入演题机械训练。利用多媒体教 学手段和Mathematica等数学软件,帮助学生体会、学习和做数学。 2、加强对学生学习过程管理,优化考核方法 大学生学习动机的强度、能量大小与学习效果间存在着相互影响的关系,教师对学生的 成绩评定是学生评价其学习效果的重要途径,为此在课程进行的过程中及时评定学生的平时 22
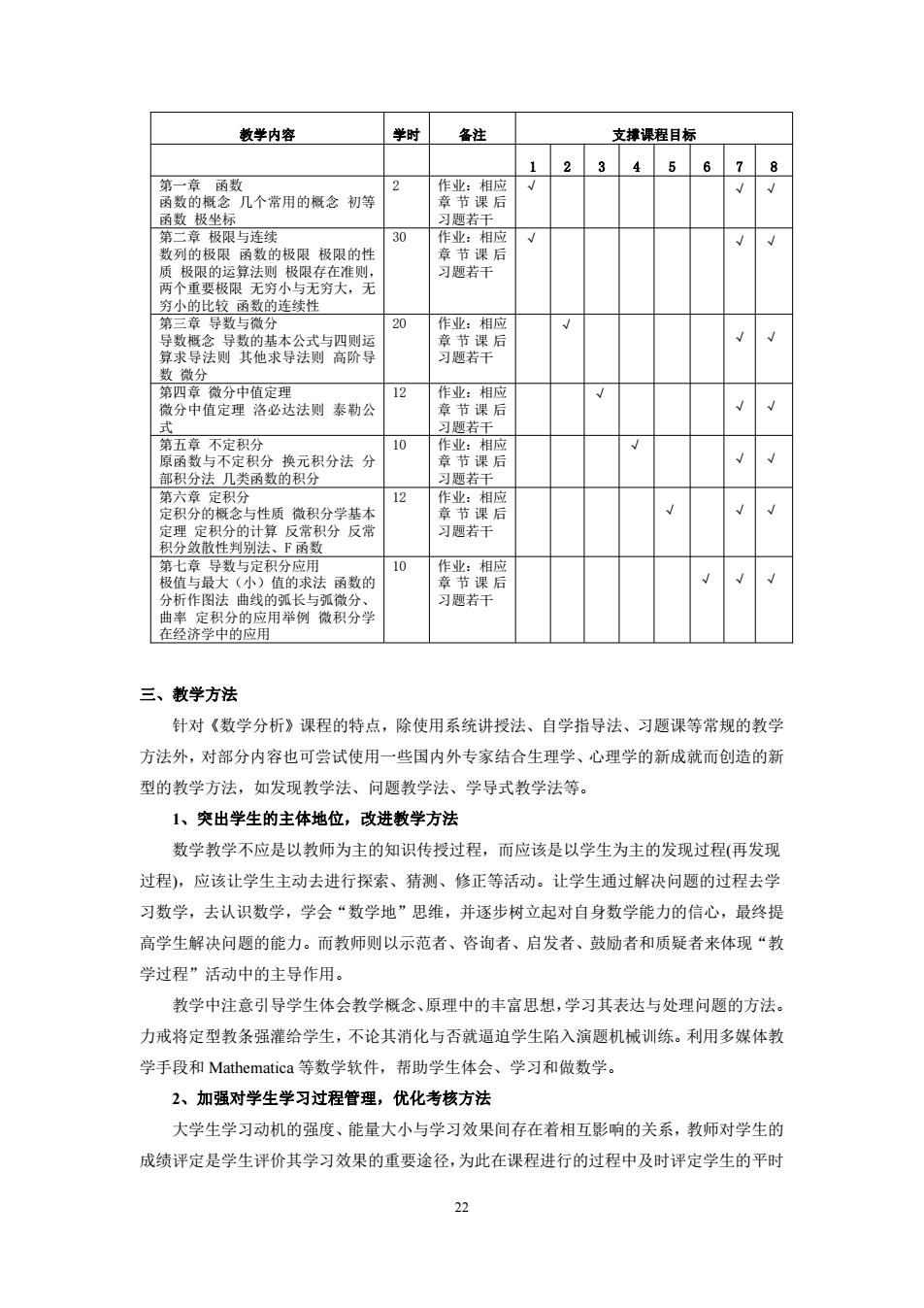
22 教学内容 学时 备注 支撑课程目标 1 2 3 4 5 6 7 8 第一章 函数 函数的概念 几个常用的概念 初等 函数 极坐标 2 作业:相应 章 节 课 后 习题若干 √ √ √ 第二章 极限与连续 数列的极限 函数的极限 极限的性 质 极限的运算法则 极限存在准则, 两个重要极限 无穷小与无穷大,无 穷小的比较 函数的连续性 30 作业:相应 章 节 课 后 习题若干 √ √ √ 第三章 导数与微分 导数概念 导数的基本公式与四则运 算求导法则 其他求导法则 高阶导 数 微分 20 作业:相应 章 节 课 后 习题若干 √ √ √ 第四章 微分中值定理 微分中值定理 洛必达法则 泰勒公 式 12 作业:相应 章 节 课 后 习题若干 √ √ √ 第五章 不定积分 原函数与不定积分 换元积分法 分 部积分法 几类函数的积分 10 作业:相应 章 节 课 后 习题若干 √ √ √ 第六章 定积分 定积分的概念与性质 微积分学基本 定理 定积分的计算 反常积分 反常 积分敛散性判别法、F 函数 12 作业:相应 章 节 课 后 习题若干 √ √ √ 第七章 导数与定积分应用 极值与最大(小)值的求法 函数的 分析作图法 曲线的弧长与弧微分、 曲率 定积分的应用举例 微积分学 在经济学中的应用 10 作业:相应 章 节 课 后 习题若干 √ √ √ 三、教学方法 针对《数学分析》课程的特点,除使用系统讲授法、自学指导法、习题课等常规的教学 方法外,对部分内容也可尝试使用一些国内外专家结合生理学、心理学的新成就而创造的新 型的教学方法,如发现教学法、问题教学法、学导式教学法等。 1、突出学生的主体地位,改进教学方法 数学教学不应是以教师为主的知识传授过程,而应该是以学生为主的发现过程(再发现 过程),应该让学生主动去进行探索、猜测、修正等活动。让学生通过解决问题的过程去学 习数学,去认识数学,学会“数学地”思维,并逐步树立起对自身数学能力的信心,最终提 高学生解决问题的能力。而教师则以示范者、咨询者、启发者、鼓励者和质疑者来体现“教 学过程”活动中的主导作用。 教学中注意引导学生体会教学概念、原理中的丰富思想,学习其表达与处理问题的方法。 力戒将定型教条强灌给学生,不论其消化与否就逼迫学生陷入演题机械训练。利用多媒体教 学手段和 Mathematica 等数学软件,帮助学生体会、学习和做数学。 2、加强对学生学习过程管理,优化考核方法 大学生学习动机的强度、能量大小与学习效果间存在着相互影响的关系,教师对学生的 成绩评定是学生评价其学习效果的重要途径,为此在课程进行的过程中及时评定学生的平时
成绩,丰富其内涵,加大其在总成绩中的比例。以激励效果好的学生,督促效果欠佳的学生 及时调整其学习态度或方法。事实上这一措施对还没有形成较强的自我管理能力的新生是十 分必要的。把两种教学方法配合运用,引导学生攻克学习难关和培养灵活运用的能力, 3、利用现代化教学手段,丰富教学手段 为了在教学中运用现代手段,突破黑板2维空间的局限,加强数学分析中的数值技术、 计算机图形和符号计算,激发学生对数学分析的兴趣,加深学生对数值技术和可应用范围的 理解,诱导学生进入更广泛的问题,可以制作和使用电子教案。 四、考核与评价方式 学生期末总成绩由两部分组成:平时成绩和期末成绩。 平时成锁占30%,其中10%为课堂表现成锁,遵守课堂规范,积极参与课堂教学活动, 认真完成小组任务,无扰乱课堂秩序的行为,计10分:10%为课后作业成绩,每次按时保质 完成课后习题作业,作业规范完整,记10分:10%为课堂随堂测验成绩,对于某些重点章节 的重点内容,可以随堂进行测验,测验方式可以是当堂出题考试,也可以是期中测试成绩 另外期末卷面成绩占70%。特别说明期末卷面成绩低于35分者,期末卷面成绩记0分。 课程目标 成锁比例(% 平时成绩 课程考试 合计 目标1 5 15 20 目标2 5 15 20 目标3 5 10 15 目标4 5 10 15 目标5 5 10 15 目标6 5 10 15 合计(成绩构成) 30 70 100 五、参考教材和阅读书目 教材:《工科数学分析》,哈尔滨工业太学数学系分折教研室编,高等教有出版社,2013 年,第四版,下册 阅读书目: 1、数学分析,陈纪修、於崇华.金路编,高等教有出版社,2000年,第一版 2、数学分析,复旦大学数学系编,高等教有出版社,1983年,年第二版 3、数学分析,华东师范大学数学系编,高等教育出版社,1991年,第二版 4.数学分析习题集,吉米多维奇,人民教育出版社,1958年,第三版
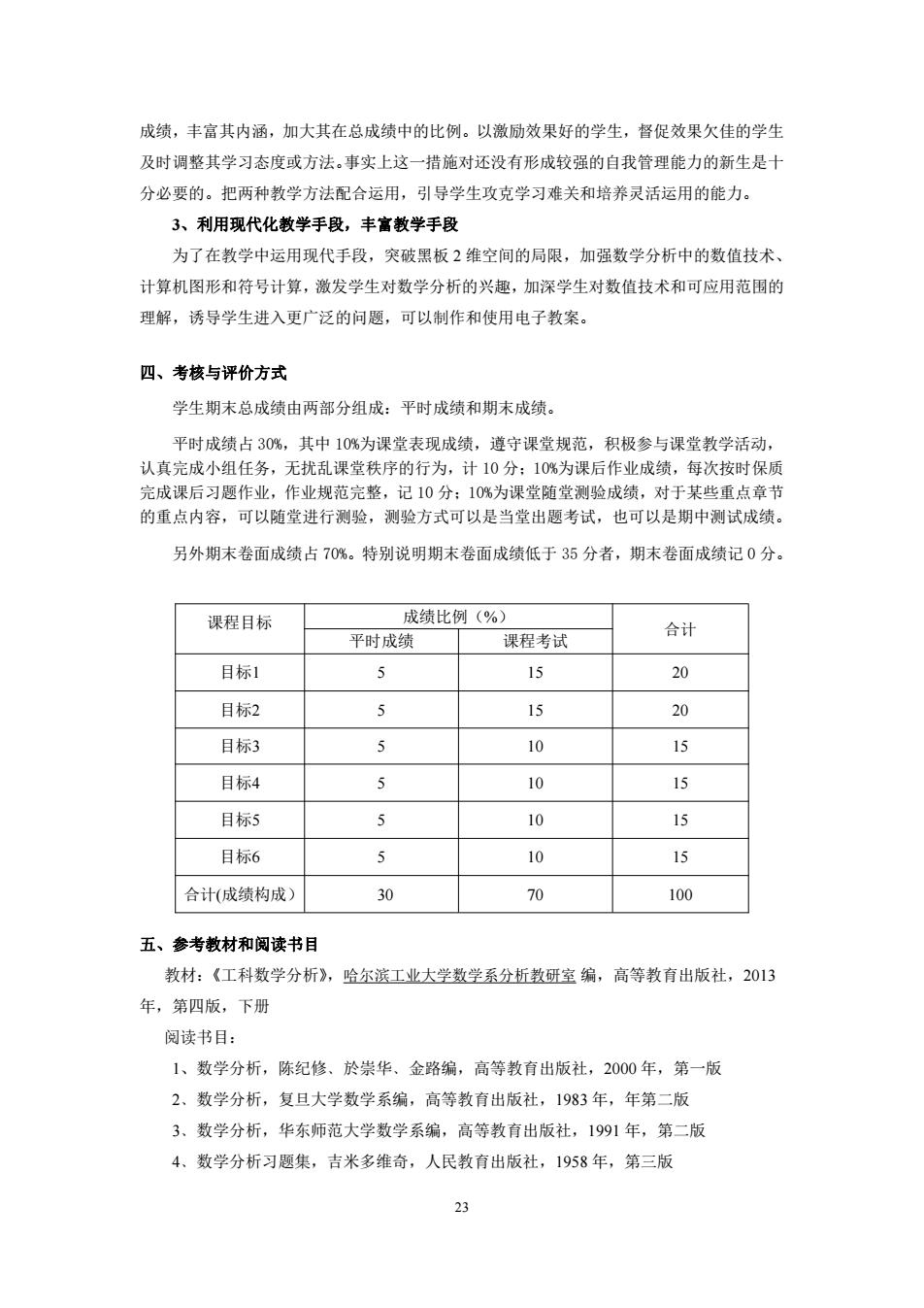
23 成绩,丰富其内涵,加大其在总成绩中的比例。以激励效果好的学生,督促效果欠佳的学生 及时调整其学习态度或方法。事实上这一措施对还没有形成较强的自我管理能力的新生是十 分必要的。把两种教学方法配合运用,引导学生攻克学习难关和培养灵活运用的能力。 3、利用现代化教学手段,丰富教学手段 为了在教学中运用现代手段,突破黑板 2 维空间的局限,加强数学分析中的数值技术、 计算机图形和符号计算,激发学生对数学分析的兴趣,加深学生对数值技术和可应用范围的 理解,诱导学生进入更广泛的问题,可以制作和使用电子教案。 四、考核与评价方式 学生期末总成绩由两部分组成:平时成绩和期末成绩。 平时成绩占 30%,其中 10%为课堂表现成绩,遵守课堂规范,积极参与课堂教学活动, 认真完成小组任务,无扰乱课堂秩序的行为,计 10 分;10%为课后作业成绩,每次按时保质 完成课后习题作业,作业规范完整,记 10 分;10%为课堂随堂测验成绩,对于某些重点章节 的重点内容,可以随堂进行测验,测验方式可以是当堂出题考试,也可以是期中测试成绩。 另外期末卷面成绩占 70%。特别说明期末卷面成绩低于 35 分者,期末卷面成绩记 0 分。 课程目标 成绩比例(%) 合计 平时成绩 课程考试 目标1 5 15 20 目标2 5 15 20 目标3 5 10 15 目标4 5 10 15 目标5 5 10 15 目标6 5 10 15 合计(成绩构成) 30 70 100 五、参考教材和阅读书目 教材:《工科数学分析》,哈尔滨工业大学数学系分析教研室 编,高等教育出版社,2013 年,第四版,下册 阅读书目: 1、数学分析,陈纪修﹑於崇华﹑金路编,高等教育出版社,2000 年,第一版 2﹑数学分析,复旦大学数学系编,高等教育出版社,1983 年,年第二版 3﹑数学分析,华东师范大学数学系编,高等教育出版社,1991 年,第二版 4﹑数学分析习题集,吉米多维奇,人民教育出版社,1958 年,第三版

5、数学分析习题精解(单变量部分),吴良森等,科学出版社,2002年,第一版 6、数学分析习题精解(多变量部分),吴良森等,科学出版社,2003年,第一版 7、工科数学分析,哈尔滨工业大学数学系分析教研室,高等教有出版社,2013年,第 四版 8、高等数学,同济大学数学系,高等教育出版社,2007年,第六版 六、本课程与其他课程的联系与分工 数学分析,是理工科学生的基础课程。对于信息学院的各理工科专业,数学分析在大学 本科教育阶段显得尤为重要,有着举足轻重的作用。该课程不但是学习复变函数、概常微分 方程、复变函数、数理方程、数值分析、概率论与数理统计等课程的必修课,而且为学习理 工科专业课程莫定必要的数学基础。 七、说明 被评为校级重点建设课程及精品课程。 撰写人:宋自根 审核人:葛焰明,袁红春 教学院长:袁红春 日期:2018-12-12
24 5、数学分析习题精解(单变量部分),吴良森等,科学出版社,2002 年,第一版 6、数学分析习题精解(多变量部分),吴良森等,科学出版社,2003 年,第一版 7、工科数学分析,哈尔滨工业大学数学系分析教研室,高等教育出版社,2013 年,第 四版 8、高等数学,同济大学数学系,高等教育出版社,2007 年,第六版 六、本课程与其他课程的联系与分工 数学分析,是理工科学生的基础课程。对于信息学院的各理工科专业,数学分析在大学 本科教育阶段显得尤为重要,有着举足轻重的作用。该课程不但是学习复变函数、概常微分 方程、复变函数、数理方程、数值分析、概率论与数理统计等课程的必修课,而且为学习理 工科专业课程奠定必要的数学基础。 七、说明 被评为校级重点建设课程及精品课程。 撰写人 :宋自根 审核人:葛焰明,袁红春 教学院长:袁红春 日期:2018-12-12

《数学分析2》教学大纲(理论课) 课程名称(中文/英文):数学分析2/Mathematic Analysis2课程编号:1103415 学分:5 学时:总学时96 学时分配:讲授学时:96 课程负贵人:戚婧 二、课程简介 1.概述 数学分析》是信息与计算科学和空间信息与数字技术等学科的一门主干基础课和必修 课。本课程的目的是为后继课程提供必要的知识,同时通过本课程的教学,锻炼和提高学生 的思维能力,培养学生掌握分析问题和解决问题的思想方法。本课程不仅对许多后继课程的 学习有直接影响,而且对学生基本功的训练与良好素质的培养起着十分重要的作用。特别是 对学生的抽象的思维、严谨的推理和一丝不萄的作风的形成和提高是其它课程难以替代的。 本课程分数学分析】1和数学分析2两个学期讲授。 analys basic cours red course o comput eceis e the students'ability of thinking training students to grasp the problem and solve the problem of thinking.This course not only has a direct impact on the learning of many subseguent courses.but also plays an important role in the training of students'basic skills and the cultivation of good quality.In particular,the formation and improvement of students'abstract thinking,rigorous reasoning and meticulous style is difficult to replace by other courses.This course is divided into two semesters. 2.教学目标 数学分析是高等学校理工科专业重要的基础理论课。该课程的主要作用,一是为后继课 程提供必需的基础数学知识:二是传授数学思想,培养学生的创新意识,逐步提高学生的数 学素养、数学思维能力和应用数学的能力。通过本课程的学习,要使学生系统的空间解析几 何、多元微积分 无穷级数与常微分方程的基本理论、基本运算和分析方法,为学习专业课 程和进一步扩大数学知识奠定必要的数学基础 具体教学目标可以概括为以下5点: (1)掌握多元函数偏导数和全微分的计算,掌握复合函数一阶、二阶偏导数的求法,会求隐 函数的偏导数。 理解方向导数与梯度的概念,掌握其计算方法。了解曲线的切线和法平面、曲面的切平面和 法线,会求它们的方程。理解多元函数极值与条件极值的概念 。了解多元函数极值存在的 要条件。会求二元函数的极值,会用拉格朗日乘数法求条件极值,会求一些简单的最大值与 最小值的应用问题。 (2②)掌握二重积分在直角坐标系和极坐标系下的计算方法,掌握三重积分在直角坐标系、柱 面坐标系、球面坐标系下的计算方法。掌握两类曲线积分的计算法,熟练掌握格林公式及曲
25 《数学分析 2》教学大纲(理论课) 课程名称(中文/英文):数学分析 2/Mathematic Analysis 2 课程编号:1103415 学 分:5 学 时:总学时 96 学时分配:讲授学时:96 课程负责人:戚婧 二、课程简介 1. 概述 《数学分析》是信息与计算科学和空间信息与数字技术等学科的一门主干基础课和必修 课。本课程的目的是为后继课程提供必要的知识,同时通过本课程的教学,锻炼和提高学生 的思维能力,培养学生掌握分析问题和解决问题的思想方法。本课程不仅对许多后继课程的 学习有直接影响,而且对学生基本功的训练与良好素质的培养起着十分重要的作用。特别是 对学生的抽象的思维、严谨的推理和一丝不苟的作风的形成和提高是其它课程难以替代的。 本课程分数学分析 1 和数学分析 2 两个学期讲授。 "Mathematical analysis" is a basic course and required course of information and computing science and space information and digital technology. The purpose of this course is to provide the necessary knowledge for subsequent courses, and through the course of teaching, exercise and improve the students' ability of thinking, training students to grasp the problem and solve the problem of thinking. This course not only has a direct impact on the learning of many subsequent courses, but also plays an important role in the training of students' basic skills and the cultivation of good quality. In particular, the formation and improvement of students' abstract thinking, rigorous reasoning and meticulous style is difficult to replace by other courses. This course is divided into two semesters. 2.教学目标 数学分析是高等学校理工科专业重要的基础理论课。该课程的主要作用,一是为后继课 程提供必需的基础数学知识;二是传授数学思想,培养学生的创新意识,逐步提高学生的数 学素养、数学思维能力和应用数学的能力。通过本课程的学习,要使学生系统的空间解析几 何、多元微积分、无穷级数与常微分方程的基本理论、基本运算和分析方法,为学习专业课 程和进一步扩大数学知识奠定必要的数学基础。 具体教学目标可以概括为以下 5 点: (1)掌握多元函数偏导数和全微分的计算,掌握复合函数一阶、二阶偏导数的求法,会求隐 函数的偏导数。 理解方向导数与梯度的概念,掌握其计算方法。了解曲线的切线和法平面、曲面的切平面和 法线,会求它们的方程。理解多元函数极值与条件极值的概念。了解多元函数极值存在的必 要条件。会求二元函数的极值,会用拉格朗日乘数法求条件极值,会求一些简单的最大值与 最小值的应用问题。 (2) 掌握二重积分在直角坐标系和极坐标系下的计算方法,掌握三重积分在直角坐标系、柱 面坐标系、球面坐标系下的计算方法。掌握两类曲线积分的计算法,熟练掌握格林公式及曲