
信息与计算科学18版教学大纲
1 信息与计算科学 18 版教学大纲

《高等代数》教学大纲(理论课) 课程名称(中文英文):高等代数(Advanced Algebra I)课程编号:I102125 时:总学时64 学时分配:讲授学时:64实验学时:0上机学时:0讨论学时:0其他学时:0 课程负责人:肖启华 一、 课程简介 1.课程概况(中、英文) 《高等代数1》是高等院校理工科专业的一门重要基础课,是中学代数的继续提高和升 华,对学生数学思想的形成有若重要的意义,是教有部规定的理工科院校最重要的公共基础 课之一。通过本课程的学习,使学生初步掌握较系统的代数知识和抽象严格的代数方法,掌 握矩阵、行列式、线性空间等现代科学描述问题的工具,为进一步学习后继课程打下基础、 为从事数据分析工作打下基础。 Advanced Algebra isone of the important and basic courses of application Mathematics Specialty in colleges and universities.The course content refine the content of middle school algebra,The course isof great significance for students toform mathematical thinking.This course is one of the most important public basic courses in science and engineering colleges stipulated by the Ministry of Education.Through the study of this course,students can grasp more systematic algebraic knowledge and abstract and strict algebraic methods,master modern further study of the follow-up courses,and lay a foundation for data analysis work. 2.课程目标: 课程目标1:行列式、矩阵、矩阵的逆、线性方程组、向量组的相关性、向量组的秩、 矩阵的秩等概念是现代数学描述问题的工具,理解和掌握上述概念及理论和基本理论,为后 继课程学习提供基础。 课程目标2:熟练掌捏行列式计算、矩阵运算、求矩阵的逆矩阵和秩、解线性方程组 判断向量组的线性相关性、求向量组的秩和最大线性无关组等方法,为后继课程的学习打下 基础。 课程目标3:理解数据概念,掌握多项式理论:掌握整除与重因式概念,会求不同多项 式的最大公因式,为学习后继内容打下基础
2 《高等代数 I》教学大纲(理论课) 课程名称(中文/英文):高等代数(Advanced Algebra I) 课程编号:1102125 学 分:4 学 时:总学时 64 学时分配:讲授学时:64 实验学时:0 上机学时:0 讨论学时:0 其他学时:0 课程负责人:肖启华 一、 课程简介 1. 课程概况(中、英文) 《高等代数 1》是高等院校理工科专业的一门重要基础课,是中学代数的继续提高和升 华,对学生数学思想的形成有着重要的意义,是教育部规定的理工科院校最重要的公共基础 课之一。通过本课程的学习,使学生初步掌握较系统的代数知识和抽象严格的代数方法,掌 握矩阵、行列式、线性空间等现代科学描述问题的工具,为进一步学习后继课程打下基础、 为从事数据分析工作打下基础。 Advanced Algebra is one of the important and basic courses of application Mathematics Specialty in colleges and universities. The course content refine the content of middle school algebra, The course is of great significance for students to form mathematical thinking, This course is one of the most important public basic courses in science and engineering colleges stipulated by the Ministry of Education.Through the study of this course, students can grasp more systematic algebraic knowledge and abstract and strict algebraic methods, master modern scientific descriptive tools such as matrix, determinant, linear space and so on, lay a foundation for further study of the follow-up courses, and lay a foundation for data analysis work. 2. 课程目标: 课程目标 1:行列式、矩阵、矩阵的逆、线性方程组、向量组的相关性、向量组的秩、 矩阵的秩等概念是现代数学描述问题的工具,理解和掌握上述概念及理论和基本理论,为后 继课程学习提供基础。 课程目标 2:熟练掌握行列式计算、矩阵运算、求矩阵的逆矩阵和秩、解线性方程组、 判断向量组的线性相关性、求向量组的秩和最大线性无关组等方法,为后继课程的学习打下 基础。 课程目标 3:理解数据概念,掌握多项式理论:掌握整除与重因式概念,会求不同多项 式的最大公因式,为学习后继内容打下基础

课程目标4:提高运用代数方法分析和解决与实际问题的能力,为使用数学方法分析处 理数据问题打下基础,为学习后继课程、进行科学研究和实际工作提供适用的数学方法和计 算手段。对数据分析工作者应该具备的职业道德、职业操守和规范有正确的理解。 课程目标5:通过课程的逻辑性与严谨性的训练逐步培养学生坚持真理、一丝不苟、实 事求是的科学态度,培养学生的诚信观念。通过数学解题的探求,使学生体验到挫折和失败, 磨练学生的心理品质,引起他们的求知欲和好奇心,使学生形成不怕困难、坚忍不拔、刻苦 钻研、顽强拼搏的优秀品格。通过培养学生的数学意识和应用数学的能力,逐步培养学生理 论联系实际的作风。 课程目标与毕业要求的关系矩阵 毕业要求 1 2 3 6 课程目标1 课程目标2 课程目标3 课程目标4 课程目标5 二、 教学内容 理论教学安排 教学内容 学备注 支排课程目标 时 1 2345 第二章行列式 18行列式 S1、引言(了解行列式概念的引出及应用) 作业若 2、排列(了解排列、排列的逆序数、偶排列与奇 排列的概念与性质) S3、n级行列式(掌握n级行列式的定义:掌捏双 角形行列式的性质) 54、n级行列式的性质(热练掌握行列式的性质: 会用这些性质简化行列式的计算) §5、行列式的计算(然练掌握行列式的计算方法) 6、行列式按一行(列)展开(掌握余子式及代数
3 课程目标 4:提高运用代数方法分析和解决与实际问题的能力,为使用数学方法分析处 理数据问题打下基础,为学习后继课程、进行科学研究和实际工作提供适用的数学方法和计 算手段。对数据分析工作者应该具备的职业道德、职业操守和规范有正确的理解。 课程目标 5:通过课程的逻辑性与严谨性的训练逐步培养学生坚持真理、一丝不苟、实 事求是的科学态度,培养学生的诚信观念。通过数学解题的探求,使学生体验到挫折和失败, 磨练学生的心理品质,引起他们的求知欲和好奇心,使学生形成不怕困难、坚忍不拔、刻苦 钻研、顽强拼搏的优秀品格。通过培养学生的数学意识和应用数学的能力,逐步培养学生理 论联系实际的作风。 课程目标与毕业要求的关系矩阵 毕业要求 1 2 3 6 7 8 课程目标 1 √ √ 课程目标 2 √ √ √ 课程目标 3 √ √ 课程目标 4 √ √ 课程目标 5 √ √ √ √ 二、 教学内容 理论教学安排 教学内容 学 时 备注 支撑课程目标 1 2 3 4 5 第二章 行列式 §1、引言(了解行列式概念的引出及应用) §2、排列(了解排列、排列的逆序数、偶排列与奇 排列的概念与性质) §3、n 级行列式(掌握 n 级行列式的定义;掌握对 角形行列式的性质) §4、n 级行列式的性质(熟练掌握行列式的性质; 会用这些性质简化行列式的计算) §5、行列式的计算(熟练掌握行列式的计算方法) §6、行列式按一行(列)展开(掌握余子式及代数 18 行 列 式 作 业 若 干 √ √ √

余子式的概念:熟练草提行列式技一行(列)展开定理) S7、Cramer法则(熟练幸提Craner法则及应用) S8、LaD1ace定理,行列式的乘法规则(选进)(堂 捏行列式的k级子式和k级子式的余子式、代数余子式的概 念:熟练掌提Laplace定理及其应用) 第三章线性方程组 20线性方 §1、消元法(了解线性方程组初等变换的概念及性 程组作 质:熟练掌握利用初等变换(消元法)解线性方程组的方法 业若干 紫握齐次线性方程组有非零解的条件) S2、n维向量空间(熟练幸握数域P上的n维向量 的概念及运算规则:了解数域P上的维向量空间的概念) §3、线性相关性(了解线性组合、线性表出以及两 个向量组等价的概念:熟练掌握向量组线性相关、线性无关 的概念:了解向量组线性相关性与齐次线性方程组解的关 系:掌握向量组线性相关与线性无关的基本性质:会求向量 组的极大线性无关组与秩) §4、矩阵的秩(然练掌握矩阵秩的概念,齐次线出 方程组系数矩阵的秩与齐次线性方程有无非零解的关系: 握矩阵k级子式的概念及矩阵秩为r的充分必要条件:熟练 举握计算矩阵秩的方法) §5、线性方程组有解判别定理(掌握线性方程组有 解判别定理) §6、线性方程组解的结构(掌握齐次线性方程组解 的性质及基础解系的概念:熟练掌界求齐次线性方程组基础 解系的方法:掌握非齐次线性方程组解的结构定理) 第四章矩阵 16矩阵作 §1、矩阵的概念(了解提出矩阵概念的问题及矩 业若干 概念) 罩2、矩阵的运算(熟练掌握矩阵的加法、乘法、数 量乘法及矩阵的转置定义及性质) $3、矩阵乘积的行列式与秩(掌捉矩阵乘积的行列 4
4 余子式的概念;熟练掌握行列式按一行(列)展开定理) §7、Cramer 法则(熟练掌握 Cramer 法则及应用) §8、Laplace 定理,行列式的乘法规则(选讲)(掌 握行列式的 k 级子式和 k 级子式的余子式、代数余子式的概 念;熟练掌握 Laplace 定理及其应用) 第三章 线性方程组 §1、消元法(了解线性方程组初等变换的概念及性 质;熟练掌握利用初等变换(消元法)解线性方程组的方法; 掌握齐次线性方程组有非零解的条件) §2、n 维向量空间(熟练掌握数域 P 上的 n 维向量 的概念及运算规则;了解数域 P 上的 n 维向量空间的概念) §3、线性相关性(了解线性组合、线性表出以及两 个向量组等价的概念;熟练掌握向量组线性相关、线性无关 的概念;了解向量组线性相关性与齐次线性方程组解的关 系;掌握向量组线性相关与线性无关的基本性质;会求向量 组的极大线性无关组与秩) §4、矩阵的秩(熟练掌握矩阵秩的概念,齐次线性 方程组系数矩阵的秩与齐次线性方程有无非零解的关系;掌 握矩阵 k 级子式的概念及矩阵秩为 r 的充分必要条件;熟练 掌握计算矩阵秩的方法) §5、线性方程组有解判别定理(掌握线性方程组有 解判别定理) §6、线性方程组解的结构(掌握齐次线性方程组解 的性质及基础解系的概念;熟练掌握求齐次线性方程组基础 解系的方法;掌握非齐次线性方程组解的结构定理) 20 线性方 程组作 业若干 √ √ √ √ 第四章 矩阵 §1、矩阵的概念(了解提出矩阵概念的问题及矩阵 概念) §2、矩阵的运算(熟练掌握矩阵的加法、乘法、数 量乘法及矩阵的转置定义及性质) §3、矩阵乘积的行列式与秩(掌握矩阵乘积的行列 16 矩阵作 业若干 √ √ √
式与秩和它的因子的行列式与秩的关系) S4、矩阵的逆(掌捏矩阵A可逆及逆矩阵的概念 了解件随矩阵与逆矩阵的关系:了解可逆矩阵与矩阵乘积的 逆与秩的关系) §5、矩阵的分块(了解分块矩阵及分块矩阵的运算 线律及应用) §6、初等矩阵(选讲)(掌握初等矩阵的概念与性 质:掌握矩阵等价的概念、任一矩阵都与其标准形等价:掌 握初等变换与初等矩阵的关系及矩阵A与B等价的充要条 件:熟练掌捏求逆矩阵的方法) 第一章多项式 10多项式 §1、数域(了解数域的概念与性质) 作业若 52、一元多项式(了解多项式的概念:掌提多项式 的运算及性质:了解一元多项式环的概念) §3、整除的概念(熟练掌捏整除的概念与性质:掌 程带余除法定理及证明) 4.最大公因式(掌捏最大公因式的概念与求法(辆 转相除法):热练掌摆多项式互素的概念与性质) §5、因式分解定理(热练掌握不可约多项式的概色 与性质:冀握因式分解及唯一性定理) §6、重因式(草握重因式的概念:肇提判别多项式 F(x)有无重因式的方法) 幸57、多项式函数(选讲)(掌提余数定理、根与 次因式的关系:了解P[x]中n次多项式在数域P中的根不 可能多于n个) ◆$8复系数与实系数多项式的因式分解(选讲)( 解代数基本定理、复系数多项式因式分解定理、实系数多项 式因式分解定理) *9、有埋系数多项式(选讲)(握本原多项式的 概念及性质:掌握求整系数多项式有理根的理论与方法:了 解Eisenstein判别法)
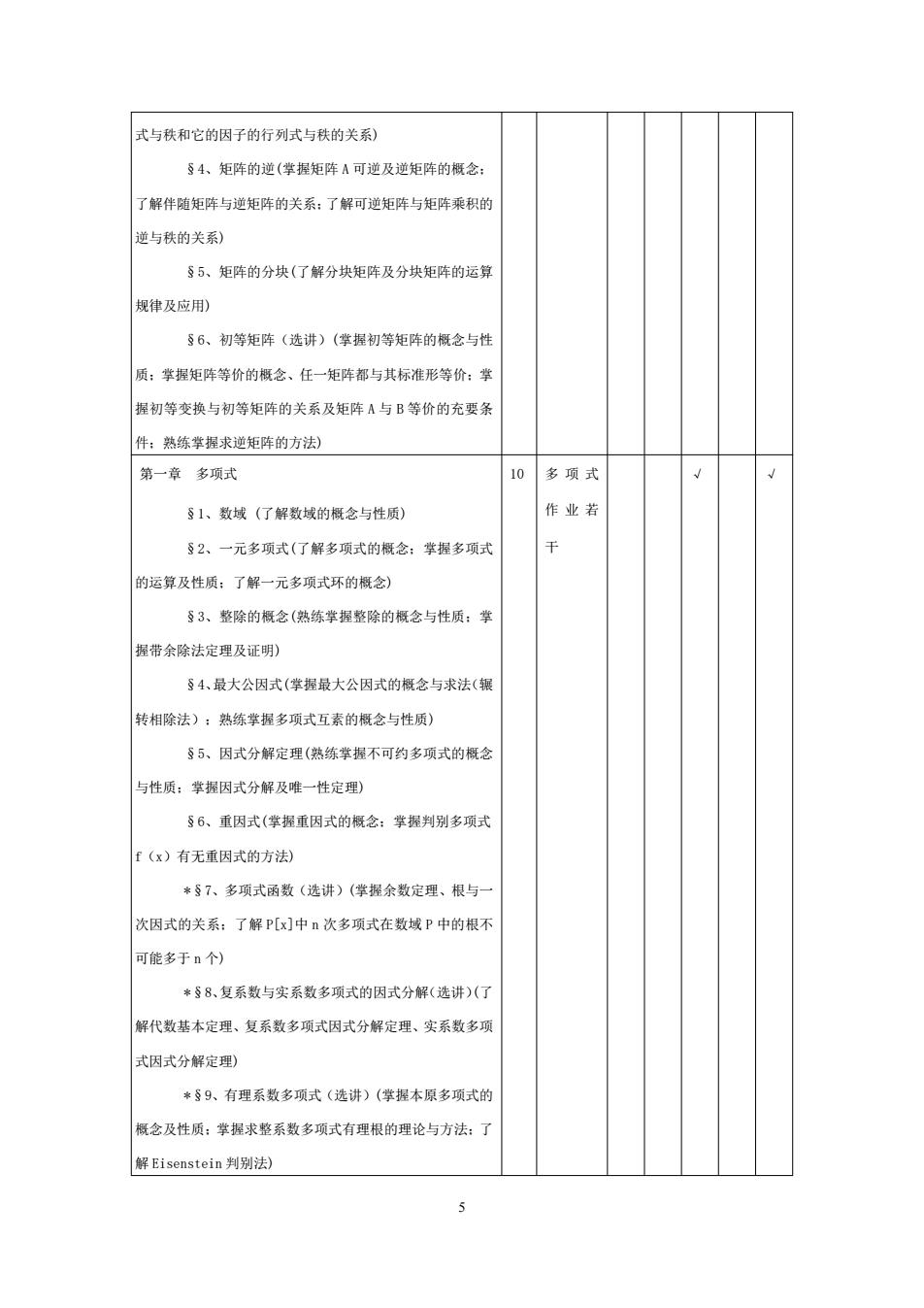
5 式与秩和它的因子的行列式与秩的关系) §4、矩阵的逆(掌握矩阵 A 可逆及逆矩阵的概念; 了解伴随矩阵与逆矩阵的关系;了解可逆矩阵与矩阵乘积的 逆与秩的关系) §5、矩阵的分块(了解分块矩阵及分块矩阵的运算 规律及应用) §6、初等矩阵(选讲)(掌握初等矩阵的概念与性 质;掌握矩阵等价的概念、任一矩阵都与其标准形等价;掌 握初等变换与初等矩阵的关系及矩阵 A 与 B 等价的充要条 件;熟练掌握求逆矩阵的方法) 第一章 多项式 §1、数域 (了解数域的概念与性质) §2、一元多项式(了解多项式的概念;掌握多项式 的运算及性质;了解一元多项式环的概念) §3、整除的概念(熟练掌握整除的概念与性质;掌 握带余除法定理及证明) §4、最大公因式(掌握最大公因式的概念与求法(辗 转相除法);熟练掌握多项式互素的概念与性质) §5、因式分解定理(熟练掌握不可约多项式的概念 与性质;掌握因式分解及唯一性定理) §6、重因式(掌握重因式的概念;掌握判别多项式 f(x)有无重因式的方法) *§7、多项式函数(选讲)(掌握余数定理、根与一 次因式的关系;了解 P[x]中 n 次多项式在数域 P 中的根不 可能多于 n 个) *§8、复系数与实系数多项式的因式分解(选讲)(了 解代数基本定理、复系数多项式因式分解定理、实系数多项 式因式分解定理) *§9、有理系数多项式(选讲)(掌握本原多项式的 概念及性质;掌握求整系数多项式有理根的理论与方法;了 解 Eisenstein 判别法) 10 多 项 式 作 业 若 干 √ √