
《解析几何》教学大纲 课程名称(中文/英文):解析几何/Analytic Geometry 课程编号:1102704 学分:2 学时:32 学时分配:讲授学时:32 课程负责人:戚结 一、课程简介 1,课程概述 解析几何是几何学的一个分支,是通过坐标法运用较初等的代数工具研究几何学问题的一门 学科。它把数学的两个基本对象一一空间形式和数量关系密切地联系起来,使得几何、代数、 分析构成一个有机的整体,为数学的其他分支与几何学的互相渗透、互相促进莫定基础。它 是从完全凭空间直观的古典几何学迈向抽象几何学的重要一步。 Analytical geometry is a branch of geometry.It is a subject to study geometry problems by using elementary algebraic tools through coordinate method.It closely links the two basic objects of Mathematics-space form and quantity,makes geometry, algebra and analysis form an organic whole,and lays a foundation for the mutual penetration and promotion of other branches of mathematics and geometry.It is an important step from classical geometry which is completely intuitive in space to abstract geometry. 2.教学目标 通过本课程的教学,使学生初步堂握较系统的用代数知识解决几何间题的方法,为进 步学习后继课程打下基础。正确理解解析几何的基本概念,掌握解析几何中的论证方法,获 得较孰练的演算技能和初步应用能力。具体教学目标以擱括为以下5点: (①)了解向量的基本概念,掌握向量的加、减法及数乘向量、线性关系,掌握数量积、向量 积、混合积的定义、运算及几何意义。 (②)掌握平面方程的几种类型及求平面方程的方程,掌握直线方程的几种类型及方程的求法, 了解平面与点的相关位置关系及两平面的相关位置关系,了解直线与平面、直线与直线的位 置关系。 (③)会建立平面曲线的方程、曲面的方程、空间曲线的方程。 6
16 《解析几何》教学大纲 课程名称(中文/英文): 解析几何/Analytic Geometry 课程编号:1102704 学 分:2 学 时:32 学时分配:讲授学时:32 课程负责人:戚婧 一、课程简介 1.课程概述 解析几何是几何学的一个分支,是通过坐标法运用较初等的代数工具研究几何学问题的一门 学科。它把数学的两个基本对象——空间形式和数量关系密切地联系起来,使得几何、代数、 分析构成一个有机的整体,为数学的其他分支与几何学的互相渗透、互相促进奠定基础。它 是从完全凭空间直观的古典几何学迈向抽象几何学的重要一步。 Analytical geometry is a branch of geometry. It is a subject to study geometry problems by using elementary algebraic tools through coordinate method. It closely links the two basic objects of Mathematics - space form and quantity, makes geometry, algebra and analysis form an organic whole, and lays a foundation for the mutual penetration and promotion of other branches of mathematics and geometry. It is an important step from classical geometry which is completely intuitive in space to abstract geometry. 2. 教学目标 通过本课程的教学,使学生初步掌握较系统的用代数知识解决几何问题的方法,为进一 步学习后继课程打下基础。正确理解解析几何的基本概念,掌握解析几何中的论证方法,获 得较熟练的演算技能和初步应用能力。具体教学目标可以概括为以下 5 点: (1) 了解向量的基本概念,掌握向量的加、减法及数乘向量、线性关系,掌握数量积、向量 积、混合积的定义、运算及几何意义。 (2) 掌握平面方程的几种类型及求平面方程的方程,掌握直线方程的几种类型及方程的求法, 了解平面与点的相关位置关系及两平面的相关位置关系,了解直线与平面、直线与直线的位 置关系。 (3) 会建立平面曲线的方程、曲面的方程、空间曲线的方程
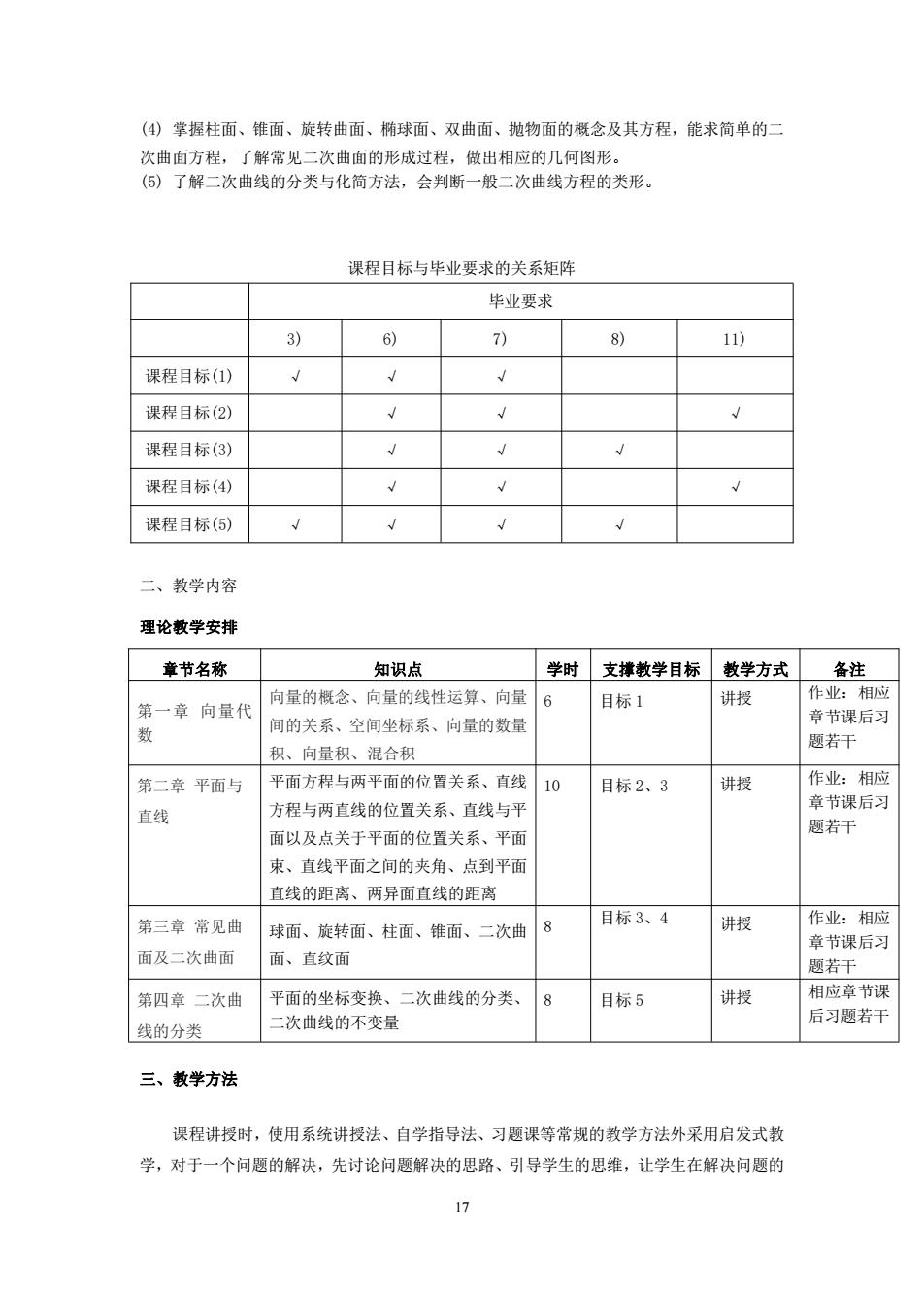
(④掌握柱面、锥面、旋转曲面、椭球面、双曲面、抛物面的概念及其方程,能求简单的二 次曲面方程,了解常见二次曲面的形成过程,做出相应的几何图形。 (⑤)了解二次曲线的分类与化简方法,会判断一般二次曲线方程的类形, 课程目标与毕业要求的关系矩阵 毕业要求 3) 6) 7) 8) 11) 课程目标(1) √ 课程目标(②) 课程目标(3) 课程目标(4) √ 课程目标(⑤) 二、教学内容 理论教学安排 章节名称 知识点 学时支撑教学目标教学方式备注 进授 作业: 应 第一章向量代 向量的概念、向量的线性运算、向量6 目标1 间的关系、空间坐标系、向量的数量 章节课后习 题若干 积、向量积、混合积 第二章平面与 平面方程与两平面的位置关系、直线 10 目标2、3 讲授 作业:相应 直线 方程与两直线的位置关系、直线与平 章节课后习 面以及点关于平面的位置关系、平面 题若干 束、直线平面之间的夹角、点到平面 直线的距离、两异面直线的距离 第三章常见曲 8 目标3、4 作业:相应 球面、旋转面、柱面、锥面、二次曲 讲授 章节课后习 面及二次曲面 面、直纹面 顺若干 第四章二次曲 平面的坐标变换、二次曲线的分类、8 进授 相应意节课 目标5 后习题若干 线的分类 二次曲线的不变量 三、教学方法 课程讲授时,使用系统讲授法、自学指导法、习题课等常规的教学方法外采用启发式教 学,对于一个问题的解决,先讨论问题解决的思路、引导学生的思维,让学生在解决问题的
17 (4) 掌握柱面、锥面、旋转曲面、椭球面、双曲面、抛物面的概念及其方程,能求简单的二 次曲面方程,了解常见二次曲面的形成过程,做出相应的几何图形。 (5) 了解二次曲线的分类与化简方法,会判断一般二次曲线方程的类形。 课程目标与毕业要求的关系矩阵 毕业要求 3) 6) 7) 8) 11) 课程目标(1) √ √ √ 课程目标(2) √ √ √ 课程目标(3) √ √ √ 课程目标(4) √ √ √ 课程目标(5) √ √ √ √ 二、教学内容 理论教学安排 章节名称 知识点 学时 支撑教学目标 教学方式 备注 第一章 向量代 数 向量的概念、向量的线性运算、向量 间的关系、空间坐标系、向量的数量 积、向量积、混合积 6 目标 1 讲授 作业:相应 章节课后习 题若干 第二章 平面与 直线 平面方程与两平面的位置关系、直线 方程与两直线的位置关系、直线与平 面以及点关于平面的位置关系、平面 束、直线平面之间的夹角、点到平面 直线的距离、两异面直线的距离 10 目标 2、3 讲授 作业:相应 章节课后习 题若干 第三章 常见曲 面及二次曲面 球面、旋转面、柱面、锥面、二次曲 面、直纹面 8 目标 3、4 讲授 作业:相应 章节课后习 题若干 第四章 二次曲 线的分类 平面的坐标变换、二次曲线的分类、 二次曲线的不变量 8 目标 5 讲授 相应章节课 后习题若干 三、教学方法 课程讲授时,使用系统讲授法、自学指导法、习题课等常规的教学方法外采用启发式教 学,对于一个问题的解决,先讨论问题解决的思路、引导学生的思维,让学生在解决问题的
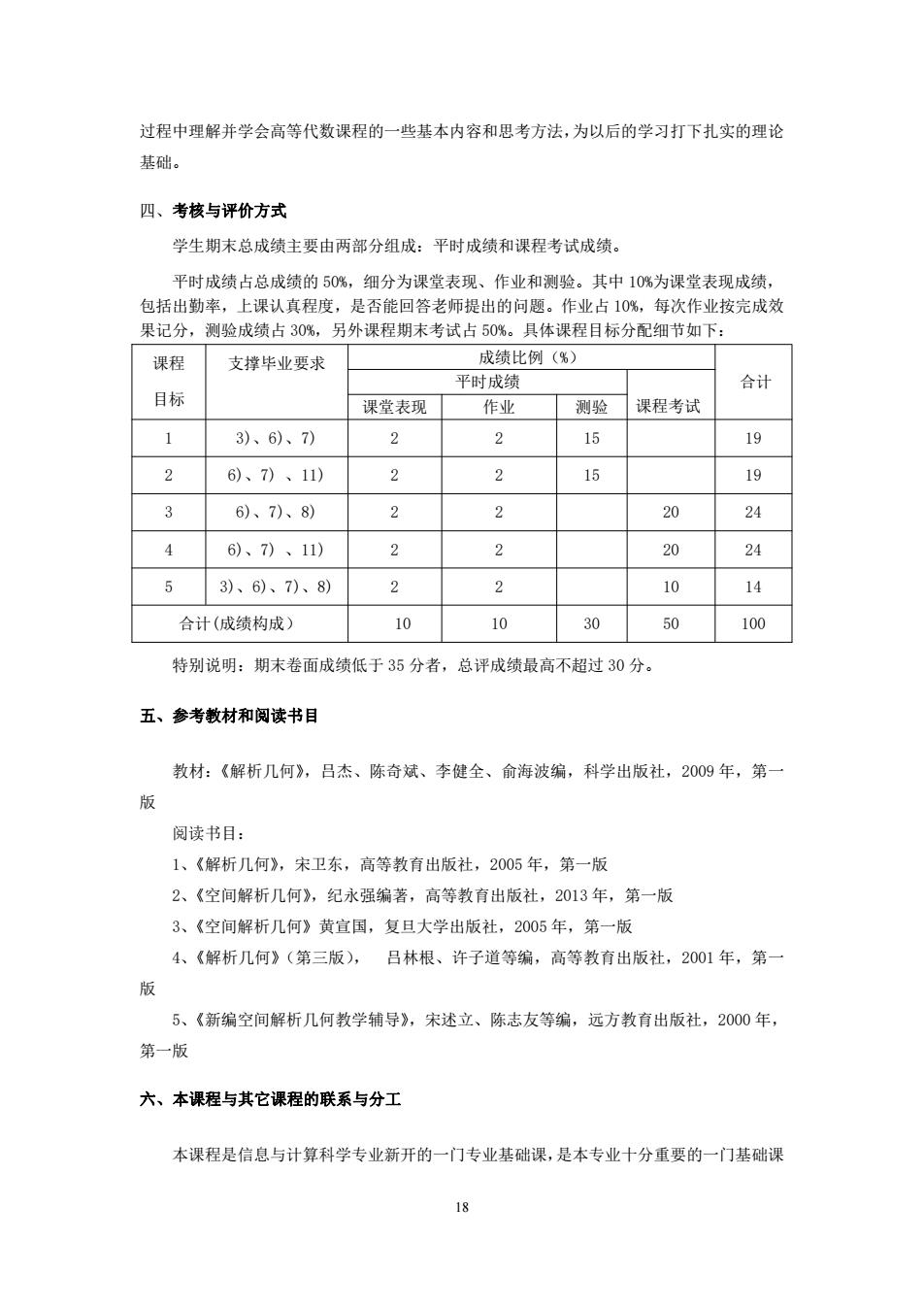
过程中理解并学会高等代数课程的一些基本内容和思考方法,为以后的学习打下扎实的理论 基础。 四、考核与评价方式 学生期末总成绩主要由两部分组成:平时成绩和课程考试成绩。 平时成绩占总成绩的5%,细分为课堂表现、作业和测验。其中10%为课堂表现成绩, 包括出勤率,上课认真程度, 是否能回答老师提出的问题。作业占10% 每次作业按完成效 果记分,测验成绩占30%,另外课程期末考试占50%。具体课程目标分配细节如下: 课程 支撑毕业要求 成绩比例(%) 平时成绩 合计 目标 课堂表现 作业 测验课程考试 1 3)、6)、7) 2 2 15 19 2 6)、7)、1) 2 2 16 9 3 6)、7)、8) 2 2 20 24 4 6)、7)、11) 2 2 20 24 53)、6)、7)、8) 2 2 10 14 合计(成绩构成) 10 10 30 50 100 特别说明:期末卷面成绩低于35分者,总评成绩最高不超过30分。 五、参考教材和阅读书目 教材:《解析几何》,吕杰、陈奇斌、李健全、俞海波编,科学出版社,2009年,第 阅读书目: 1、《解析几何》,宋卫东,高等教有出版社,2005年,第一版 2、《空间解析几何》,纪水强编著,高等教有出版社,2013年,第一版 3、《空间解析几何》黄宣国,复旦大学出版社,2005年,第一版 4、《解析几何》(第三版),吕林根、许子道等编,高等教有出版社,2001年,第 5、《新编空间解析几何教学辅导》,宋述立、陈志友等编,远方教育出版社,2000年, 第一版 六、本课程与其它课程的联系与分工 本课程是信息与计算科学专业新开的一门专业基础课,是本专业十分重要的一门基础课 18
18 过程中理解并学会高等代数课程的一些基本内容和思考方法,为以后的学习打下扎实的理论 基础。 四、考核与评价方式 学生期末总成绩主要由两部分组成:平时成绩和课程考试成绩。 平时成绩占总成绩的 50%,细分为课堂表现、作业和测验。其中 10%为课堂表现成绩, 包括出勤率,上课认真程度,是否能回答老师提出的问题。作业占 10%,每次作业按完成效 果记分,测验成绩占 30%,另外课程期末考试占 50%。具体课程目标分配细节如下: 课程 目标 支撑毕业要求 成绩比例(%) 平时成绩 合计 课堂表现 作业 测验 课程考试 1 3)、6)、7) 2 2 15 19 2 6)、7) 、11) 2 2 15 19 3 6)、7)、8) 2 2 20 24 4 6)、7) 、11) 2 2 20 24 5 3)、6)、7)、8) 2 2 10 14 合计(成绩构成) 10 10 30 50 100 特别说明:期末卷面成绩低于 35 分者,总评成绩最高不超过 30 分。 五、参考教材和阅读书目 教材:《解析几何》,吕杰、陈奇斌、李健全、俞海波编,科学出版社,2009 年,第一 版 阅读书目: 1、《解析几何》,宋卫东,高等教育出版社,2005 年,第一版 2、《空间解析几何》,纪永强编著,高等教育出版社,2013 年,第一版 3、《空间解析几何》黄宣国,复旦大学出版社,2005 年,第一版 4、《解析几何》(第三版), 吕林根、许子道等编,高等教育出版社,2001 年,第一 版 5、《新编空间解析几何教学辅导》,宋述立、陈志友等编,远方教育出版社,2000 年, 第一版 六、本课程与其它课程的联系与分工 本课程是信息与计算科学专业新开的一门专业基础课,是本专业十分重要的一门基础课

程。 本课程的任务是介绍解析几何的方法和基本知识,培养学生运用解析几何方法解决几何问题 的能力、空间想象能力及在实际问题中运用解析几何的知识和方法的能力,并为以后学习高 等代数、数学分析和其他有关课程做准备。 七、其他 无 主撰人:戚蜻 审核人:葛焰明 袁红春 教学院长:袁红春 日期: 2018-11-30 9
19 程。 本课程的任务是介绍解析几何的方法和基本知识,培养学生运用解析几何方法解决几何问题 的能力、空间想象能力及在实际问题中运用解析几何的知识和方法的能力,并为以后学习高 等代数、数学分析和其他有关课程做准备。 七、其他 无 主撰人:戚 婧 审核人:葛焰明, 袁红春 教学院长:袁红春 日 期: 2018-11-30

《数学分析1》教学大纲 课程名称(中文英文):数学分析1 Mathematic Analysis1 课程编号:110341 学分:5 学时:总学时96 学时分配(讲授学时:96) 课程负责人:宋自根 一、课程简介 1.课程概述 《数学分析》是信总与计算科学和空间信总与数字技术等学科的一门主干基础课和必修 课。本课程的目的是为后继课程提供必要的知识,同时通过本课程的教学,锻炼和提高学生 的思维能力,培养学生掌握分析间题和解决问题的思想方法。本课程不仅对许多后继课程的 学习有直接影响,而且对学生基本功的训练与良好素质的培养起者十分重要的作用。特别是 对学生的抽象的思维、严谨的推理和一丝不苟的作风的形成和提高是其它课程难以替代的。 本课程分数学分析1和数学分析2两个学期讲授。 "Mathematical analysis"is a basic course and required course of information and computing science and space information and digital technology.The purpose of this course is to provide the necessary knowledge for subsequent courses,and through the course of teaching.exercise and improve the students ability of thinking.training students to grasp the problem and solve the problem of thinking This couse hasadirect impacton the eaming of many subsequent courses.but also plays an important role in the training of students basic skills and the cultivation of good quality.In particular,the formation and improvement of students'abstract thinking. rigorous reasoning and meticulous style is difficult to replace by other courses.This course is divided into two semesters 2.课程目标 课程目标1:重点掌握初等函数类函数及其性质,理解极限概念及其精确的数学定义 掌握极限的性质及四则运算法则,学会用严格数学语言论证极限问题。熟练掌握计算极限的 方法,无穷小及其阶的比较,连续和间断的概念和性质,理解函数在一点连续的概念及初等 函数连续性。 课程目标2:理解导数与微分的概念,并了解其几何意义及函数的可导性与连续性之间 的关系。能熟练地运用导数定义与求导法则(特别是复合函数求导法则)求函数导数的导数。 掌握基本初等函数的导数公式。会用求导公式求某些简单函数的高阶导数 20
20 《数学分析 1》教学大纲 课程名称(中文/英文):数学分析 1/Mathematic Analysis 1 课程编号:1103411 学 分:5 学 时:总学时 96 学时分配(讲授学时: 96) 课程负责人:宋自根 一、课程简介 1. 课程概述 《数学分析》是信息与计算科学和空间信息与数字技术等学科的一门主干基础课和必修 课。本课程的目的是为后继课程提供必要的知识,同时通过本课程的教学,锻炼和提高学生 的思维能力,培养学生掌握分析问题和解决问题的思想方法。本课程不仅对许多后继课程的 学习有直接影响,而且对学生基本功的训练与良好素质的培养起着十分重要的作用。特别是 对学生的抽象的思维、严谨的推理和一丝不苟的作风的形成和提高是其它课程难以替代的。 本课程分数学分析 1 和数学分析 2 两个学期讲授。 "Mathematical analysis" is a basic course and required course of information and computing science and space information and digital technology. The purpose of this course is to provide the necessary knowledge for subsequent courses, and through the course of teaching, exercise and improve the students' ability of thinking, training students to grasp the problem and solve the problem of thinking. This course not only has a direct impact on the learning of many subsequent courses, but also plays an important role in the training of students' basic skills and the cultivation of good quality. In particular, the formation and improvement of students' abstract thinking, rigorous reasoning and meticulous style is difficult to replace by other courses. This course is divided into two semesters. 2.课程目标 课程目标 1:重点掌握初等函数类函数及其性质,理解极限概念及其精确的数学定义, 掌握极限的性质及四则运算法则,学会用严格数学语言论证极限问题。熟练掌握计算极限的 方法,无穷小及其阶的比较,连续和间断的概念和性质,理解函数在一点连续的概念及初等 函数连续性。 课程目标 2:理解导数与微分的概念,并了解其几何意义及函数的可导性与连续性之间 的关系。能熟练地运用导数定义与求导法则(特别是复合函数求导法则)求函数导数的导数。 掌握基本初等函数的导数公式。会用求导公式求某些简单函数的高阶导数