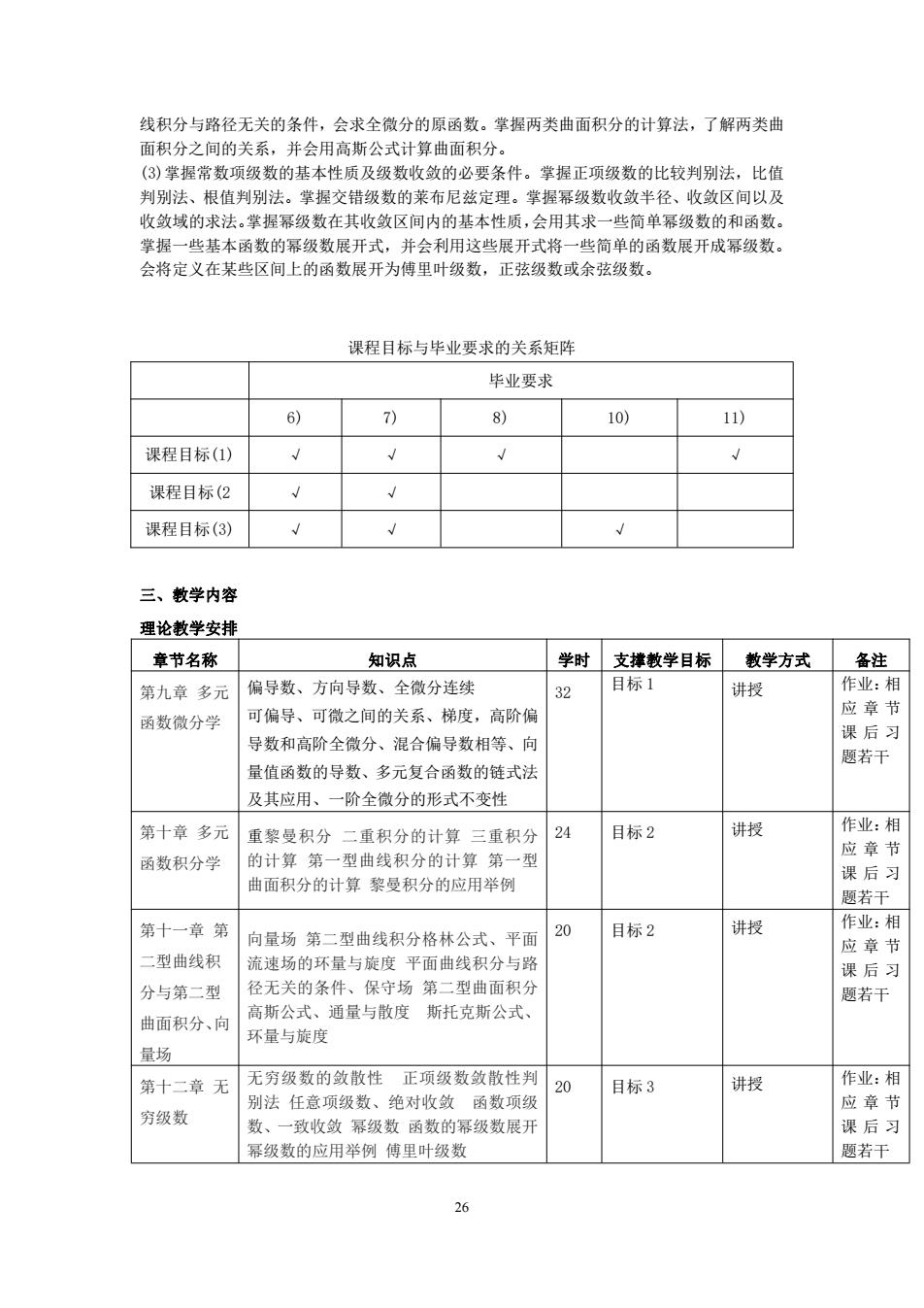
线积分与路径无关的条件,会求全微分的原函数。掌握两类曲面积分的计算法,了解两类曲 面积分之间的关系,并会用高斯公式计算曲面积分。 (3)掌握常数项级数的基本性质及级数收敛的必要条件。掌握正项级数的比较判别法,比值 判别法、根值判别法。掌握交错级数的莱布尼兹定理。掌握幂级数收敛半径、收敛区间以及 收敛域的求法。掌握幂级数在其收敛区间内的基本性质,会用其求一些简单幂级数的和函数。 掌握一些基本函数的幂级数展开式,并会利用这些展开式将一些简单的函数展开成幂级数。 会将定义在某些区间上的函数展开为傅里叶级数,正弦级数或余弦级数。 课程目标与毕业要求的关系矩阵 毕业要求 6) 7) 8) 10) 11) 课程目标(1) √ 课程目标(2 课程目标(3) 三、教学内容 理论教学安排 章节名称 知识点 学时支排教学目标 学方式 备注 第九章多元偏导数、方向导数、全微分连续 32 讲授 作 函数微分学 可偏导、可微之间的关系、梯度,高阶偏 课后习 导数和高阶全微分、混合偏导数相等、向 题若干 量值函数的导数、多元复合函数的链式沙 及其应用、一阶全微分的形式不变性 第十章多元 目标2 讲授 作业:相 重黎曼积分二重积分的计篁三重积分24 函数积分学 的计算第一型曲线积分的计算第一型 应章节 曲面积分的计算黎曼积分的应用举例 课后习 题若干 第十一章第 向量场第二型曲线积分格林公式、平面 20 目标2 讲授 作业:相 应音节 二型曲线积 流速场的环量与旋度平面曲线积分与路 课后习 分与第二型 径无关的条件、保守场第二型曲面积分 题若干 曲面积分、向 高斯公式、通量与散度斯托克斯公式、 环量与旋度 量场 第十二章无 无穷级数的敛散性正项级数敛散性判 20 目标3 讲授 作业:相 别法任意项级数、绝对收敛函数项级 应章节 穷级数 一致收敛幂级数函数的幂级数展开 课后习 幂级数的应用举例傅里叶级数 题若干
26 线积分与路径无关的条件,会求全微分的原函数。掌握两类曲面积分的计算法,了解两类曲 面积分之间的关系,并会用高斯公式计算曲面积分。 (3)掌握常数项级数的基本性质及级数收敛的必要条件。掌握正项级数的比较判别法,比值 判别法、根值判别法。掌握交错级数的莱布尼兹定理。掌握幂级数收敛半径、收敛区间以及 收敛域的求法。掌握幂级数在其收敛区间内的基本性质,会用其求一些简单幂级数的和函数。 掌握一些基本函数的幂级数展开式,并会利用这些展开式将一些简单的函数展开成幂级数。 会将定义在某些区间上的函数展开为傅里叶级数,正弦级数或余弦级数。 课程目标与毕业要求的关系矩阵 毕业要求 6) 7) 8) 10) 11) 课程目标(1) √ √ √ √ 课程目标(2 √ √ 课程目标(3) √ √ √ 三、教学内容 理论教学安排 章节名称 知识点 学时 支撑教学目标 教学方式 备注 第九章 多元 函数微分学 偏导数、方向导数、全微分连续 可偏导、可微之间的关系、梯度,高阶偏 导数和高阶全微分、混合偏导数相等、向 量值函数的导数、多元复合函数的链式法 及其应用、一阶全微分的形式不变性 32 目标 1 讲授 作业:相 应 章 节 课 后 习 题若干 第十章 多元 函数积分学 重黎曼积分 二重积分的计算 三重积分 的计算 第一型曲线积分的计算 第一型 曲面积分的计算 黎曼积分的应用举例 24 目标 2 讲授 作业:相 应 章 节 课 后 习 题若干 第十一章 第 二型曲线积 分与第二型 曲面积分、向 量场 向量场 第二型曲线积分格林公式、平面 流速场的环量与旋度 平面曲线积分与路 径无关的条件、保守场 第二型曲面积分 高斯公式、通量与散度 斯托克斯公式、 环量与旋度 20 目标 2 讲授 作业:相 应 章 节 课 后 习 题若干 第十二章 无 穷级数 无穷级数的敛散性 正项级数敛散性判 别法 任意项级数、绝对收敛 函数项级 数、一致收敛 幂级数 函数的幂级数展开 幂级数的应用举例 傅里叶级数 20 目标 3 讲授 作业:相 应 章 节 课 后 习 题若干

三、教学方法 针对《数学分析》课程的特点,除使用系统讲授法、自学指导法、习题课等常规的教学 方法外,对部分内容也可尝试使用一些国内外专家结合、生理学心理学的新成就而创造的新 型的教学方法,如发现教学法、问题教学法、学导式教学法等。 四、考核与评价方式 学生期末总成绩主要由两部分组成:平时成绩和课程考试成绩。 平时成绩占总成绩的40%,细分为课堂表现、作业和测验。其中10%为课堂表现成绩 包括出勤率,上课认其程度,是否能回答老师提出的问题。作业占15%,每次作业按完成效 果记分,测验成绩占15%,另外课程期末考试占60%。具体课程目标分配细节如下: 课程 支掉毕业要求 成绩比例() 平时成绩 课程考 合计 目标 课堂表现 作业 测验 试 1 6)、7)、8)、11) 3 5 10 18 36 6)、7) 4 5 5 24 38 3 6)、7)、10 5 18 26 合计(成绩构成) 10 15 1560 100 特别说明:期末卷面成绩低于35分者,总评成绩最高不超过30分 五、参考教材和阅读书目 教材:《工科数学分析》,哈尔滨工业大学数学系分析教研室编,高等教有出版社,2013 年,第四版,下册 阅读书目: 1、数学分析,陈纪修、於崇华。金路编,高等教育出版社,2000年,第一版 2.数学分析,复旦大学数学系编,高等教育出版社,1983年,年第二版 3、数学分析,华东师范大学数学系编,高等教育出版社,1991年,第二版 4、数学分析习题集,吉米多维奇,人民教有出版社,1958年,第三版 5、数学分析习题精解(单变量部分),吴良森等,科学出版社,2002年,第一版 6、数学分析习题精解(多变量部分),吴良森等,科学出版社,2003年,第一版 7、工科数学分析,哈尔滨工业大学数学系分析教研室,高等教有出版社,2013年,第 四版 8、高等数学,同济大学数学系,高等教有出版社,2007年,第六版 大、本课程与其他课程的联系与分工
27 三、教学方法 针对《数学分析》课程的特点,除使用系统讲授法、自学指导法、习题课等常规的教学 方法外,对部分内容也可尝试使用一些国内外专家结合、生理学心理学的新成就而创造的新 型的教学方法,如发现教学法、问题教学法、学导式教学法等。 四、考核与评价方式 学生期末总成绩主要由两部分组成:平时成绩和课程考试成绩。 平时成绩占总成绩的 40%,细分为课堂表现、作业和测验。其中 10%为课堂表现成绩, 包括出勤率,上课认真程度,是否能回答老师提出的问题。作业占 15%,每次作业按完成效 果记分,测验成绩占 15%,另外课程期末考试占 60%。具体课程目标分配细节如下: 课程 目标 支撑毕业要求 成绩比例(%) 平时成绩 课程考 合计 课堂表现 作业 测验 试 1 6)、7)、8)、11) 3 5 10 18 36 2 6)、7) 4 5 5 24 38 3 6)、7)、10) 3 5 18 26 合计(成绩构成) 10 15 15 60 100 特别说明:期末卷面成绩低于 35 分者,总评成绩最高不超过 30 分。 五、参考教材和阅读书目 教材:《工科数学分析》,哈尔滨工业大学数学系分析教研室 编,高等教育出版社,2013 年,第四版,下册 阅读书目: 1、数学分析,陈纪修﹑於崇华﹑金路编,高等教育出版社,2000 年,第一版 2﹑数学分析,复旦大学数学系编,高等教育出版社,1983 年,年第二版 3﹑数学分析,华东师范大学数学系编,高等教育出版社,1991 年,第二版 4﹑数学分析习题集,吉米多维奇,人民教育出版社,1958 年,第三版 5、数学分析习题精解(单变量部分),吴良森等,科学出版社,2002 年,第一版 6、数学分析习题精解(多变量部分),吴良森等,科学出版社,2003 年,第一版 7、工科数学分析,哈尔滨工业大学数学系分析教研室,高等教育出版社,2013 年,第 四版 8、高等数学,同济大学数学系,高等教育出版社,2007 年,第六版 六、本课程与其他课程的联系与分工

数学分析,是理工科学生的基础课程。对于以信息和数技处理为主的信息学院的各理工 科专业,数学分析在大学本科教有阶段显得尤为重要,有着举足轻重的作用。该课程不但是 学习复变函数、概常微分方程、复变函数、数理方程、数值分析、概率论与数理统计等课程 的必修课,而且为学习理工科专业课程奠定必要的数学基础。 七、说明 无 撰写人:戚婧 审核人:葛焰 明,袁红春 教学院长:袁红春 日期: 2018-12-30 28
28 数学分析,是理工科学生的基础课程。对于以信息和数技处理为主的信息学院的各理工 科专业,数学分析在大学本科教育阶段显得尤为重要,有着举足轻重的作用。该课程不但是 学习复变函数、概常微分方程、复变函数、数理方程、数值分析、概率论与数理统计等课程 的必修课,而且为学习理工科专业课程奠定必要的数学基础。 七、说明 无 撰写人:戚 婧 审核人:葛焰 明,袁红春 教学院长:袁红春 日 期: 2018-12-30

《复变函数》教学大纲(理论课) 课程名称(中文/英文):复变函数(Complex Analysis)课程编号:104104 学分:3学分 8学时 学时分配讲 48 课程负责人:刘海 一、课程简介 1.课程概况(中、英文) 《复变函数》(又名复分析)是理工科大学生的一门专业基础选修课。复分析既与数学 的众多学科有着紧密的联系,如代数、几何以及调和分析等。同时,又在工程技术领域有者 广泛的应用,如流体力学、电学、磁学、信号处理以及热传导等方面。本课程旨在向学生介 绍复变函数的基本理论和方法,通过实例展示其在现代工程科技上的应用,为学生应用复方 法解决工程问题打下坚实的基础。内容包括:复数、解析函数、初等函数、复积分、解析函 数的级数表示、留数理论、共形映照以及积分变换。 Complex Analysis is a basic course for the undergraduate that studies the science and harmonic such as fluid mechanics,electricity,magnetism,signal processing and heat conduction etc.This course aims to introduce students to the basic theories and methods of complex function,and show them its applications in modern engineering science and technology.It lays a solid foundation for students to apply complex methods to solve engineering problems.The course will discuss ytic function,complex integration,complex series,residues theorem 2.课程目标 课程目标1:通过课程学习,学生应了解复数及复变函数论的发展历程。理解并掌握复 变函数论的基本概念和重要结论,包括复数的代数表示 三角表示、指数表示及三者之间的 转换。熟练竿握复数的四则运算及儿何意义,理解各初等函数的性质及与实变函数的区别和 联系等: 课程目标2:掌握解析函数的概念及性质,理解并会运用C-R方程判断所给函数是否解 析。具备基本的计算复积分、解析函数的无穷级数展开以及留数的能力,了解共形映射的理 论及在其他学科应 课程目标3 了解复变函数在现代工程技术中的应用,通过复分析在流体力学、电学 磁学、信号处理、热传导方面的应用实例的学习,能够初步利用复方法解决实际问题: 课程目标4:掌握积分变换的基本性质及运算,了解其在微分方程及信号处理等领域的 应用。通过课程学习,开阔视野,拓宽知识面,培养一定的数学素质。 课程目标5:通过数学的严谨证明,培养学生坚持真理事实求是的科学态度:通过简洁 结论和深刻优美的论证引起学生的求知欲和好奇心:通过简单的函数关系和复杂图像,培养 学生的审美意识和创造能力:
29 《复变函数》教学大纲(理论课) 课程名称(中文/英文):复变函数(Complex Analysis) 课程编号: 1104104 学分:3学分 学时:总学时 48学时 学时分配:讲授学时:48 课程负责人:刘海峰 一、 课程简介 1. 课程概况(中、英文) 《复变函数》(又名复分析)是理工科大学生的一门专业基础选修课。复分析既与数学 的众多学科有着紧密的联系,如代数、几何以及调和分析等。同时,又在工程技术领域有着 广泛的应用,如流体力学、电学、磁学、信号处理以及热传导等方面。本课程旨在向学生介 绍复变函数的基本理论和方法,通过实例展示其在现代工程科技上的应用,为学生应用复方 法解决工程问题打下坚实的基础。内容包括:复数、解析函数、初等函数、复积分、解析函 数的级数表示、留数理论、共形映照以及积分变换。 Complex Analysis is a basic course for the undergraduate that studies the science and engineer. It is closely related to many disciplines of mathematics, such as algebra, geometry, and harmonic analysis. Complex analysis is also widely used in the field of engineering technology, such as fluid mechanics, electricity, magnetism, signal processing and heat conduction etc. This course aims to introduce students to the basic theories and methods of complex function, and show them its applications in modern engineering science and technology. It lays a solid foundation for students to apply complex methods to solve engineering problems. The course will discuss complex number, analytic function, complex integration, complex series, residues theorem, conformal mapping and integral transformation. 2. 课程目标 课程目标 1:通过课程学习,学生应了解复数及复变函数论的发展历程。理解并掌握复 变函数论的基本概念和重要结论,包括复数的代数表示、三角表示、指数表示及三者之间的 转换。熟练掌握复数的四则运算及几何意义,理解各初等函数的性质及与实变函数的区别和 联系等; 课程目标 2:掌握解析函数的概念及性质,理解并会运用 C-R 方程判断所给函数是否解 析。具备基本的计算复积分、解析函数的无穷级数展开以及留数的能力,了解共形映射的理 论及在其他学科应用; 课程目标 3:了解复变函数在现代工程技术中的应用,通过复分析在流体力学、电学、 磁学、信号处理、热传导方面的应用实例的学习,能够初步利用复方法解决实际问题; 课程目标 4:掌握积分变换的基本性质及运算,了解其在微分方程及信号处理等领域的 应用。通过课程学习,开阔视野,拓宽知识面,培养一定的数学素质。 课程目标 5:通过数学的严谨证明,培养学生坚持真理事实求是的科学态度;通过简洁 结论和深刻优美的论证引起学生的求知欲和好奇心;通过简单的函数关系和复杂图像,培养 学生的审美意识和创造能力
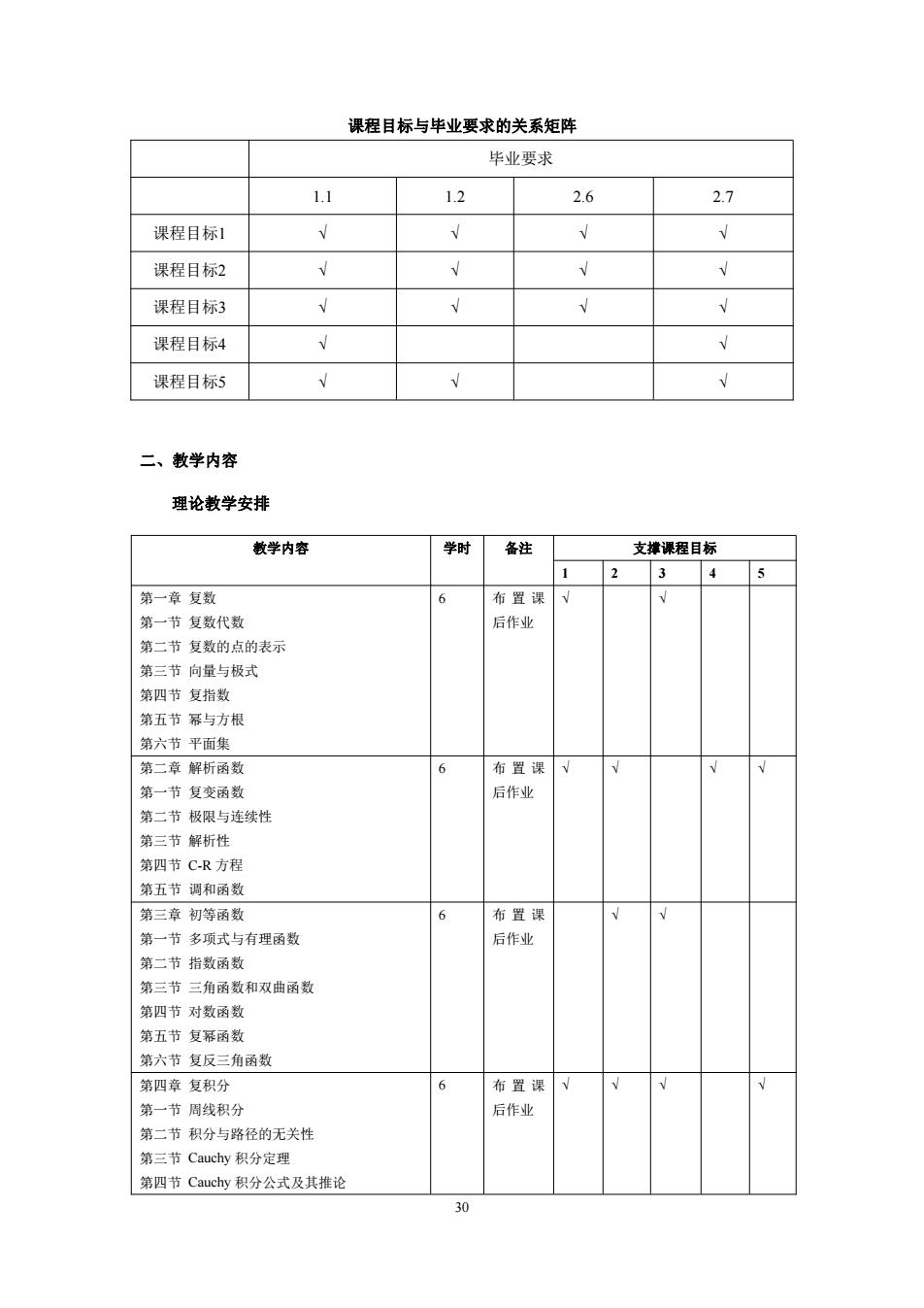
课程目标与毕业要求的关系矩阵 毕业要求 1.1 12 2.6 27 课程目标1 课程目标2 课程目标3 课程目标4 课程目标5 二、教学内容 理论教学安排 散学内容 学时备注 支撞课程目标 4 第一章复数 布置课 第一节复数代数 后作业 第二节复数的点的表示 第三节向量与极式 第四节复指数 第五节幂与方根 第六节平面集 第二章解析函数 6 布置课√ 第一节复变函数 后作业 第二节极限与连续性 第三节解析性 第四节CR方程 第五节调和函数 第三章初等承数 布置课 第一节多项式与有理函数 后作业 第二节指数函数 第三节三角函数和双曲函数 第四节对数函数 第五节复幂函数 第六节复反三角函数 第四章复积分 布置课 第一节周线积分 后作业 第二节积分与路径的无关性 第三节Cauchv积分定理 第四节Cauchy积分公式及其推论
30 课程目标与毕业要求的关系矩阵 毕业要求 1.1 1.2 2.6 2.7 课程目标1 √ √ √ √ 课程目标2 √ √ √ √ 课程目标3 √ √ √ √ 课程目标4 √ √ 课程目标5 √ √ √ 二、教学内容 理论教学安排 教学内容 学时 备注 支撑课程目标 1 2 3 4 5 第一章 复数 第一节 复数代数 第二节 复数的点的表示 第三节 向量与极式 第四节 复指数 第五节 幂与方根 第六节 平面集 6 布 置 课 后作业 √ √ 第二章 解析函数 第一节 复变函数 第二节 极限与连续性 第三节 解析性 第四节 C-R 方程 第五节 调和函数 6 布 置 课 后作业 √ √ √ √ 第三章 初等函数 第一节 多项式与有理函数 第二节 指数函数 第三节 三角函数和双曲函数 第四节 对数函数 第五节 复幂函数 第六节 复反三角函数 6 布 置 课 后作业 √ √ 第四章 复积分 第一节 周线积分 第二节 积分与路径的无关性 第三节 Cauchy 积分定理 第四节 Cauchy 积分公式及其推论 6 布 置 课 后作业 √ √ √ √