
Background B.2 Sinusoids 6 ■Example B.5 Is the period.For the sinusoid in Eq.(B.18),C is the amplltude,Fo is the Consider Fw)a complex function of a real variablew: frequeney (in Hertz),and is the phase.Let us consider two special cases of this =#器 sinusoid when 6=0 and =-/2 as follows: (B,16a) (a)f)=Ccos2rFat (0=0) (b)f(t)=Ccos (C sin 2nFot (9=-2 (a)To obtain the real and imaginary parts of F(w),we must eliminate imaginary terms in the denominator ofF)This is readily done by multiplying both the merato degree or radians.Although and denominator of F(w)by 3-jdw,the conjugate of the denominator 3+f4w so that per un use th -得+8瑞-6-总-品 Fa (B.16b) 24 419 example doub blem or ar This is the Cartesian form of F()Clearly the renl and imnginary partsF)and F() are given by It is ento use the variable(radian frequency)to express Fu)-g+16 g=2x B.20) (b) With this notation,the sinusoid in Eq.(B.18)can be expressed as 9+ f()=C cos (oat+0) in which the period To is given by see Eqs.(B.19)and (B.20) 4+w2 (B.16c) 1 (B.21a This is the representation of F).Observe that and 一完 (B.21b) F=am(假)-tam(学) (B.17) In future shall ofe refertoas the frequency of the signa ◆ but it should be clearly understood that the frequency of this sinusod B.2 Sinusoids 4 and B.6b re an be rea g the Consider the sinusoid signal Ccos in Fig.B.6a by the appropriate amount. Consider,for example f0=Ccos(2m列4+) B.18) f(t)=C cos (wot-60) We know that This ned so (Fig.B.6a) co6p=c0s(p+2nxn=0,士1,±2,土3,. ya phase gle)of 360 one cycle. Therefore,cosp repeats itself for every change of 2 in the angle.For the .4 sinusoid in Ea.(B.18),the angle 2sFo+changes by 2x when t changes by 1/Fo.Clearly,this sinusoid repeats every 1/Fo seconds.As a result,there are n in Flg B.6c Fo repetitions per second.This is the frequency of the sinusoid,and the repetition ve del o in Fig.B.6a interval To given by id 1 (B.19 Ccos(wot-)=Csin wot (B.22a)

Background B.2 Sinusoids Re a Pig.B.7 Phasor addition of ainusolds Therefore, C=Va2+ba (B.23b) 。=m() (B.23c) the resulting polar number are C and 6,respectively. To summarize, a cos wot+bsin wot =Ccos (wot+) Ceos(-) in which C and are given by Eqs.(B.23b)and(B.23c).respectively.These happen to be the magnitude and angle,respectively,of a-j. The process of adding two sinusoids with the same frequency can be clarified by using phasors to represent sinusoids.We represent the sinusoid Ccos(wot+) by a phasor of length C at an angle with the horizontal axis.Clearly,the sinusoid acos wot is represented by a horizontal phasor of length a(=0),while bsin o= bcoe(wot-)is represented by a vertical phasor of length b at an angle-/2 with the horizontal (Fig.B.7).Adding these two phasors results in a phasor of length C at an angle 8,as depicted in Fig.B.7.From this figure,we verify the values ofc and found in Eqs.(B.23b)and (B.23c),respectively. Fig.B.6 Sketching sinusoid. Proper care should be exercised in computing Recall that tan-() tan-1().Similarly,tan-1()#tan-1().Electronic calculators cannot make ifwedvancebyqer-eycleeobtain this distinction.When calculating such an angle,it is advisable to note the quadrant Therefore, where the angle lies and not to rely exclusively on an electronic calculator.A Csin (wot+=C oos wot (B.22b) vation means sinot lags cos by(/radians)r c leads examples clarify this point. B.2-1 Addition of Sinusoids (a)fit)cos wot -v3sin wot (b)f()=-3c0s wot+4sin wnt (a)In this case,1,and from Eqs.(B.23) Ccos (oot+)mC coscos wot-C sinsin wot C=V+(v5)=2 =a00s wot +b sin wot (B.23a in which 6=tan-1(平)=60 a=C cos b=-Csin

Background B.3 Sketching Signal山 Therefore. f)=2c08{aot+60) tedbya unit pbasor at an angle of-90 with the borizontal the horizantal (also shown in Fig.B.8a).Therefore. R二 f()=2cos (t+0) Fig.B.Phasor addition of in Example B.6 We perform the reverse operation,expresing f()=Coos (wot + f)=-2c0s(46t+60°±180) terms of coand sin using the trigonometric identity =-2cc8(uot-120) =-2ce(4ot+240) Ccos (wpt+)=C cos 6 cos wot-C sin 8 sin wot For example, In practice,anxpre with an angle whoe merical vaesthanis preferred 10 cos (wot-60)=5cos wot +5v3sin wot (b)In this ease,=-3,b=4,and from Egs.(B.23) Sinusoids in Terms of Exponentials:Euler's Formula Sinusoids can be expressed in terms of exponentials using Euler's formula see C=V-3)2+4=6 Eg.(B.31 6=t8m1(作3》m-126.91 cos (ev+e) (B.24a) Obeerve that an-1{()≠an'()-53.1 血0=方(0-e0) (B.24b) Therefore Inversion of these equations yields f(t)=(wot-126 cos+jsin B.25a T9。器A4- =c0s -fsin B,25b Hence,C 5 and =-1269. ◆ O Computer Example CB.4 B.3 Sketching Signals Express f(t)=-3co8 wot+4sin wot an a single sinusold. In this section we discuss the sketching of a few useful signals,starting with hoadgC, exponentials. the re B.3-1 Monotonic Exponentials 8=-39b4: [theta.C]mcart2pol(a.b); Theta_deg=(180/pi)"theta C,Theta-deg the sake lcity,we shail arting at t B.10 s1 1 the valne d z.B.10a.This rops to ntial ps to about 7%of -3cou+4sin wot=5cos(wot-16.) ⊙
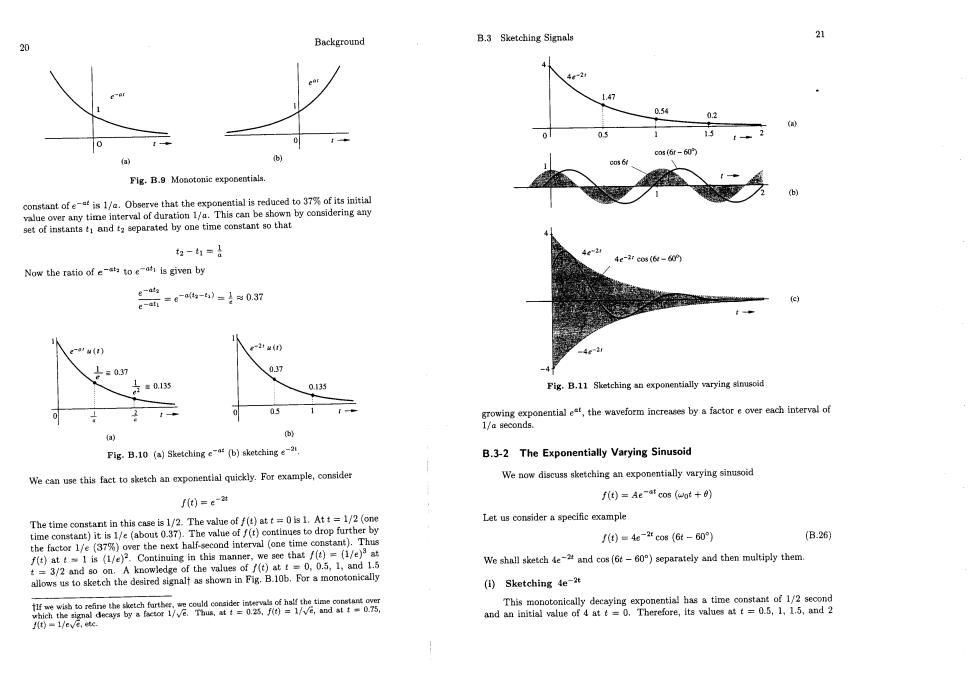
Background B.3 Sketching Signals 21 4 4e-2 60 (bi Flg.B.9 Monotonic expopentials. etugGmAa1and2eparatdbyonetimecohstantsohg t妇-t1=} 4e-2r cos (6 Now the ratio given by 。=64-=0.37 e-M( ruir) =0.37 0.37 -4 =0,135 0.35 Fig.B.11 Sketching exponentially varying snusoid 05 1 the ire byfactoreenro Fig.B.10 (a)Sketching e (b)sketching e B.3-2 The Exponentially Varying Sinusoid We can use this fact to sketch an exponential quickly.For example,conside We now discuss sketching an exponentially varying sinusoid f(t)=e-t f(t)=Ae-at cos (wot +0) The time constant in this cnse is 1/2.The value off()att=0is1.Att=1/2(one Let us consider a specific example time constant)it is 1/e (abo 0t0.37 alue of f(t)continues to drop further by cond interval(one time constant).Thus f④=4e-2cos(6t-60) (B.26) the factor 1/e (37% we see that f(t)=(1/e)at t 3/2 and so on. of the values of f(t)at t=0,0.5,1,and 1.5 We shall sketch e and cos(6t-60)separately and then multiply them. allowsuto sketch the desired signalf as shown in Fig.B.10b.For a monotonically (1)Sketching 4e-t This monotonically deeaying exponential has a time co nt of 1/2 se and an initial value of 4 at t=0.Therefore,Its values at t=0.5.1.1.5,and 2 (t)-1/eve,ate

Background B.4 Cramer's Rule 2 e2,4/e,and 4/e4,or about 1.47,0.54,0.2.and g.o7 respectively.U 「1 evalues as a guide,we sketch 4e ed in Fig B.118. [a1a12a1 21a+ 420 (ii)Sketching cos(6t-60) (B.30) The proc cedure for sketching cs(6)is discussed in Se.B.2(Fig.B.6c) Here the peno soid isTo=2/61,and there is a phase delay of rter-cycle,which is equivalent to about n(60/360)(1)1/6 ig,B.11b), We denote the matrix on the left-hand side forme by the aonaahesetof s A.The determinant of A is denoted by Al.If the de A G20 (Sketching 4e-tcos(6t-60) equations(B.29)has a unique solution given by Cramer's We now multiply the wavefors in(i)and ()The mutiplication amounts to forcing the amplitude of thes exponetiallywitha Dal k=1,2,n (B.31) ng to 4/e(=1.47) time constant ot U.o.Ihe att=0.5,tol.47fe(=0, This is depicted in Fig.B.11e where D is obtained by replacing the kth column of Al by the column on the Note that at the instants where cos(6t- 0)h a value of unity (peak amplitude). right-hand side of Eq.(B.30)(with elements We shall demonstrate the use of this rule with an example 4-2#cs(6-60)=4e1 (B27) ■Example B.T Therefore, e)instants where Using Cramer's rule,ove the following three un- )ethe knowns: 21+2+工8=3 60)has a value of-1(negative peak amplitude). 工1+3a2-约=7 4-c0s(6t-60)=-4-2 (B28) eaks.Therefore,-4e-2 an envelope for negative amplitudes Thus.to sketch e-2 co (660),we first draw the en opes 二e(the mirrormag T2111[1 3 of 4eabout the horizontal axis ,and h the e ginusoid cos(6t-60°),witt these envelopes acting as constraints on the litude (see Fig.B.11e). In general.Kea cos (wot+8)can be s this manner,with Ke-at and 111JL」 Here, -Ke constraining the amplitude of cos (+) 1211 A=13-1=4 B.4 Cramer's Rule 111 olution existsforand.This solution isprovide 1311 a111十a12g+.十a1nxn=1 73-1-=2 111 a21+22r十.+2m不n= (B29 12311 ,小i1-4-101t9 a21+an22++dann= These equations can be expressed in matrix form as 111